4.4: Extension beyond sigmoid neurons
- Page ID
- 3762
We've proved that networks made up of sigmoid neurons can compute any function. Recall that in a sigmoid neuron the inputs \(x_1,x_2,…\) result in the output \(σ(\sum_j{w_jx_j+b})\),where \(w_j\) are the weights, \(b\) is the bias, and σσ is the sigmoid function:
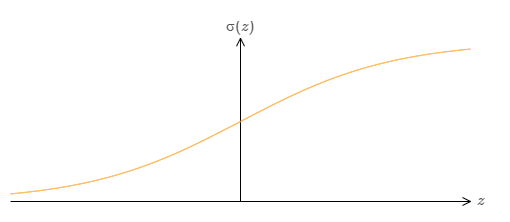
What if we consider a different type of neuron, one using some other activation function, \(s(z)\):
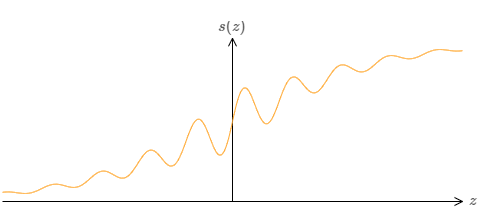
That is, we'll assume that if our neurons has inputs \(x_1,x_2,…\), weights \(w_1,w_2,…\) and bias bb, then the output is \(σ(\sum_j{w_jx_j+b})\).
We can use this activation function to get a step function, just as we did with the sigmoid. Try ramping up the weight in the following, say to \(w=100\):
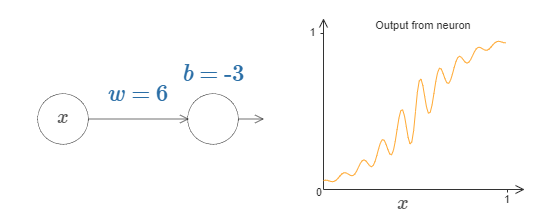
Just as with the sigmoid, this causes the activation function to contract, and ultimately it becomes a very good approximation to a step function. Try changing the bias,
and you'll see that we can set the position of the step to be wherever we choose. And so we can use all the same tricks as before to compute any desired function.
What properties does \(s(z)\) need to satisfy in order for this to work? We do need to assume that \(s(z)\) is well-defined as \(z→−∞\) and \(z→∞\). These two limits are the two values taken on by our step function. We also need to assume that these limits are different from one another. If they weren't, there'd be no step, simply a flat graph! But provided the activation function \(s(z)\) satisfies these properties, neurons based on such an activation function are universal for computation.
Problems
- Earlier in the book we met another type of neuron known as a rectified linear unit. Explain why such neurons don't satisfy the conditions just given for universality. Find a proof of universality showing that rectified linear units are universal for computation.
- Suppose we consider linear neurons, i.e., neurons with the activation function \(s(z)=z\). Explain why linear neurons don't satisfy the conditions just given for universality. Show that such neurons can't be used to do universal computation.


