3.4.2: Operations on functions
- Page ID
- 10894
Suppose that f : A → B and g: B → C are functions. Given a ∈ A, there is an associated element f (a) ∈ B. Since g is a function from B to C, and since f (a) ∈ B, g associates some element of C to f (a). That element is g( f (a)). Starting with an element a of A, we have produced an associated element g( f (a)) of C. This means that we have defined a new function from the set A to the set C. This function is called the composition of g with f , and it is denoted by g ◦ f . That is, if f : A → B and g : B → C are functions, then g ◦ f: A → C is the function which is defined by
\((g \circ f)(a)=g(f(a))\)
for each a ∈ A. For example, suppose that p is the function that associates to each item in a store the price of the item, and suppose that t is a function that associates the amount of tax on a price to each possible price. The composition, t ◦ p, is the function that associates to each item the amount of tax on that item. Or suppose that s : N → N and r: N → N are the functions defined by the formulas s(n) = n2 and r(n) = 3n + 1, for each n ∈ N. Then r ◦ s is a function from N to N, and for n ∈ N,(r◦s)(n) = \(r(s(n))=r\left(n^{2}\right)=3 n^{2}+1 .\) In this case, we also have the function \(s \circ r,\) which satisfies \((s \circ r)(n)=s(r(n))=s(3 n+1)=(3 n+1)^{2}=9 n^{2}+6 n+1 .\) Note in particular that \(r \circ s\) and s ◦ r are not the same function. The operation ◦ is not commutative. If A is a set and f : A → A, then f ◦ f , the composition of f with itself, is defined. For example, using the function s from the preceding example, s ◦ s is the function from \(\mathbb{N}\) to \(\mathbb{N}\) given by the formula \((s \circ s)(n)=s(s(n))=s\left(n^{2}\right)^{2}=n^{4} .\) If \(m\) is the function from the set of people to itself which associates to each person that person’s mother, then m ◦ m is the function that associates to each person that person’s maternal grandmother.
If a and b are entities, then (a, b) denotes the ordered pair containing a and b. The ordered pair (a, b) differs from the set {a, b} because a set is not ordered. That is, {a, b} and \(\{b, a\}\) denote the same set, but if \(a \neq b,\) then \((a, b)\) and \((b, a)\) are different ordered pairs. More generally, two ordered pairs (a, b) and (c, d) are equal if and only if both a = c and b = d. If (a, b) is an ordered pair, then a and b are referred to as the coordinates of the ordered pair. In particular, a is the first coordinate and b is the second coordinate.
In high school you would also have to write (x,y)-coordinates using this ordered pair notation. For instance you would say that the line y = ax + b intersects the y-axis at \((0, b)\) and the \(x\) -axis at \(\left(-\frac{b}{a}, 0\right)\)
If A and B are sets, then we can form the set A × B which is defined by
A × B = {(a, b) | a ∈ A and b ∈ B}.
This set is called the cross product or Cartesian product of the sets A and B. The set A × B contains every ordered pair whose first coordinate is an element of A and whose second coordinate is an element of B. For example, if X = {c, d} and Y = {1, 2, 3}, then X × Y = {(c, 1), (c, 2), (c, 3), (d, 1), (d, 2), (d, 3)}. It is possible to extend this idea to the cross product of more than two sets. The cross product of the three sets A, B, and C is denoted A × B × C. It consists of all ordered triples (a, b, c) where a ∈ A, b ∈ B, and c ∈ C. The definition for four or more sets is similar. The general term for a member of a cross product is tuple (recall page 42) or, more specifically, ordered n-tuple. For example,(a, b, c, d, e) is an ordered 5-tuple.
Given a function f: A → B, consider the set{(a,b) ∈ A×B|a ∈ A and b = f(a)}. This set of ordered pairs consists of all pairs (a, b) such that a ∈ A and b is the element of B that is associated to a by the function f . The set {(a, b) ∈ A × B | a ∈ A and b = f (a)}is called the graph of the function f . Since f is a function, each element a ∈ A occurs once and only once as a first coordinate among the ordered pairs in the graph of f . Given a ∈ A, we can determine f (a) by finding that ordered pair and looking at the second coordinate. In fact, it is convenient to consider the function and its graph to be the same thing, and to use this as our official mathematical definition.
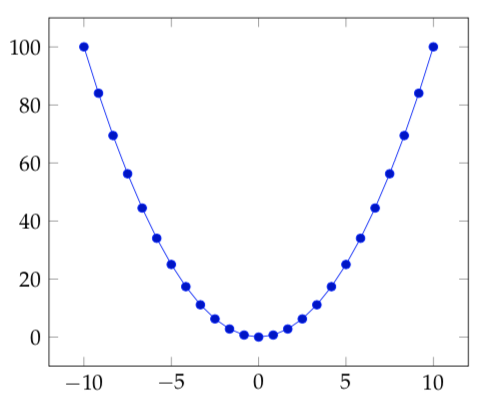
(a) Graph for the formula \(f(n)=n^{2}\) for \(-10 \leq\) \(n \leq 10\)
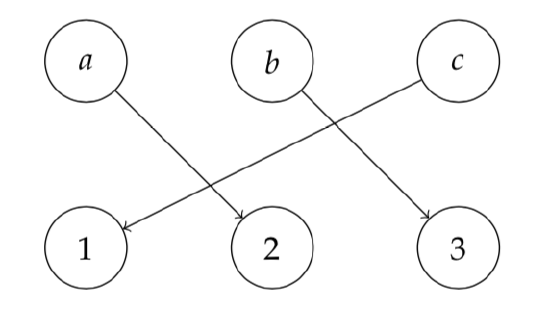
(b) Graph for the function g : A → B with A = {a,b,c} and B = {1,2,3}, such that g = {(a, 2), (b, 3), (c, 1)}.
Figure 4.7: Two different graphs representing functions.
You are already familiar with the process of graphing numerical functions from high school (for instance you can graph the formula \(f(n)=n^{2}\) as depicted in Figure 4.7a), but we can also graph non-numerical functions as indicated in Figure 4.7b. To do so, we draw all elements from the set A and connect them to the elements of B they map to.
Definition4.2.
Let A and B be sets. A function from A to B is a subset of A×B which has the property that for each a ∈ A, the set contains one and only one ordered pair whose first coordinate is a. If (a, b) is that ordered pair, then b is called the value of the function at a and is denoted f (a). If b = f (a), then we also say that the function f maps a to b. The fact that f is a function from A to B is indicated by the notation f : A → B.
For example, if X = {a,b} and Y = {1,2,3}, then the set {(a,2),(b,1)} is a function from X to Y, and {(1, a), (2, a), (3, b)} is a function from Y to X. On the other hand, {(1, a), (2, b)} is not a function from Y to X, since it does not specify any value for 3. And {(a, 1), (a, 2), (b, 3)} is not a function from X to Y because it specifies two different values, 1 and 2, associated with the same element, a, of X.
Even though the technical definition of a function is a set of ordered pairs, it’s usually better to think of a function from A to B as something that associates some element of B to every element of A. The set of ordered pairs is one way of expressing this association. If the association is expressed in some other way, it’s easy to write down the set of ordered pairs. For example, the function \(s : \mathbb{N} \rightarrow \mathbb{N}\) which is specified by the formula \(s(n)=n^{2}\) can be written as the set of ordered pairs \(\left\{\left(n, n^{2}\right) | n \in \mathbb{N}\right\}\)

