1.7: List of Data Structures

Last updated
Save as PDF

Page ID: 8434

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

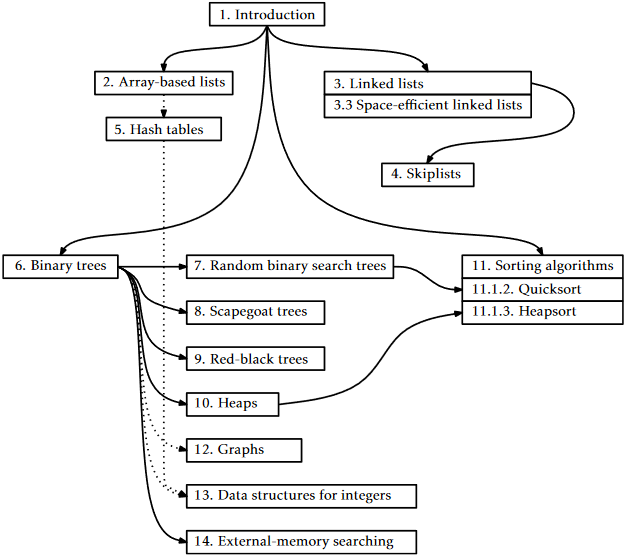
Tables \(\PageIndex{1}\) and \(\PageIndex{2}\) summarize the performance of data structures in this book that implement each of the interfaces, List, USet, and SSet, described in Section 1.2. Figure \(\PageIndex{1}\) shows the dependencies between various chapters in this book. A dashed arrow indicates only a weak dependency, in which only a small part of the chapter depends on a previous chapter or only the main results of the previous chapter.

Table \(\PageIndex{1}\): Summary of List and USet implementations.

\(\texttt{List}\) implementations

	\(\mathtt{get(i)}/\mathtt{set(i,x)}\)	\(\mathtt{add(i,x)}/\mathtt{remove(i)}\)
\(\texttt{ArrayStack}\)	\(O(1)\)	\(O(1+\mathtt{n}-\mathtt{i})\)^A	§ 2.1
\(\texttt{ArrayDeque}\)	\(O(1)\)	\(O(1+\min\{\mathtt{i},\mathtt{n}-\mathtt{i}\})\)^A	§ 2.4
\(\texttt{DualArrayDeque}\)	\(O(1)\)	\(O(1+\min\{\mathtt{i},\mathtt{n}-\mathtt{i}\})\)^A	§ 2.5
\(\texttt{RootishArrayStack}\)	\(O(1)\)	\(O(1+\mathtt{n}-\mathtt{i})\)^A	§ 2.6
\(\texttt{DLList}\)	\(O(1+\min\{\mathtt{i},\mathtt{n}-\mathtt{i}\})\)	\(O(1+\min\{\mathtt{i},\mathtt{n}-\mathtt{i}\})\)	§ 3.2
\(\texttt{SEList}\)	\(O(1+\min\{\mathtt{i},\mathtt{n}-\mathtt{i}\}/\mathtt{b})\)	\(O(\mathtt{b}+\min\{\mathtt{i},\mathtt{n}-\mathtt{i}\}/\mathtt{b})\)^A	§ 3.3
\(\texttt{SkiplistList}\)	\(O(\log \mathtt{n})\)^E	\(O(\log \mathtt{n})\)^E	§ 4.3

\(\texttt{USet}\) implementations

	\(\mathtt{find(x)}\)	\(\mathtt{add(x)}/\mathtt{remove(x)}\)
^ADenotes an amortized running time. ^EDenotes an expected running time.
\(\texttt{ChainedHashTable}\)	\(O(1)\)^E	\(O(1)\)^A,E	§ 5.1
\(\texttt{LinearHashTable}\)	\(O(1)\)^E	\(O(1)\)^A,E	§ 5.2

Table \(\PageIndex{2}\): Summary of SSet and priority Queue implementations.

\(\texttt{SSet}\) implementations

	\(\mathtt{find(x)}\)	\(\mathtt{add(x)}/\mathtt{remove(x)}\)
\(\texttt{SkiplistSSet}\)	\(O(\log \mathtt{n})\)^E	\(O(\log \mathtt{n})\)^E	§ 4.2
\(\texttt{Treap}\)	\(O(\log \mathtt{n})\)^E	\(O(\log \mathtt{n})\)^E	§ 7.2
\(\texttt{ScapegoatTree}\)	\(O(\log \mathtt{n})\)	\(O(\log \mathtt{n})\)^A	§ 8.1
\(\texttt{RedBlackTree}\)	\(O(\log \mathtt{n})\)	\(O(\log \mathtt{n})\)	§ 9.2
\(\texttt{BinaryTrie}\)^I	\(O(\mathtt{w})\)	\(O(\mathtt{w})\)	§ 13.1
\(\texttt{XFastTrie}\)^I	\(O(\log \mathtt{w})\)^A,E	\(O(\mathtt{w})\)^A,E	§ 13.2
\(\texttt{YFastTrie}\)^I	\(O(\log \mathtt{w})\)^A,E	\(O(\log \mathtt{w})\)^A,E	§ 13.3
\(\texttt{BTree}\)	\(O(\log \mathtt{n})\)	\(O(B+\log \mathtt{n})\)^A	§ 14.2
\(\texttt{BTree}\)^X	\(O(\log_B \mathtt{n})\)	\(O(\log_B \mathtt{n})\)	§ 14.2

(Priority) \(\texttt{Queue}\) implementations

	\(\mathtt{findMin()}\)	\(\mathtt{add(x)}/\mathtt{remove()}\)
^IThis structure can only store \(\texttt{w}\)-bit integer data. ^XThis denotes the running time in the external-memory model; see Chapter 14.
\(\texttt{BinaryHeap}\)	\(O(1)\)	\(O(\log \mathtt{n})\)^A	§ 10.1
\(\texttt{MeldableHeap}\)	\(O(1)\)	\(O(\log \mathtt{n})\)^E	§ 10.2

Figure \(\PageIndex{1}\): The dependencies between chapters in this book.