9.1: 2-4 Trees
- Page ID
- 8472
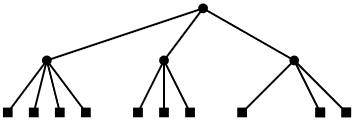
A 2-4 tree is a rooted tree with the following properties:
Property \(\PageIndex{1}\) (height).
All leaves have the same depth.
Property \(\PageIndex{2}\) (degree).
Every internal node has 2, 3, or 4 children.
An example of a 2-4 tree is shown in Figure \(\PageIndex{1}\).
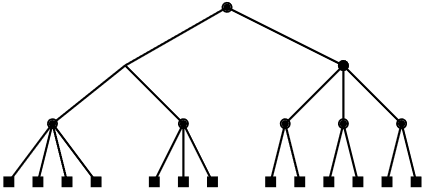
The properties of 2-4 trees imply that their height is logarithmic in the number of leaves:
A 2-4 tree with \(\mathtt{n}\) leaves has height at most \(\log \mathtt{n}\).
Proof. The lower-bound of 2 on the number of children of an internal node implies that, if the height of a 2-4 tree is \(h\), then it has at least \(2^h\) leaves. In other words,
\[ \mathtt{n} \ge 2^h \enspace . \nonumber\]
Taking logarithms on both sides of this inequality gives \(h \le \log \mathtt{n}\). ![]()
\(\PageIndex{1}\) Adding a Leaf
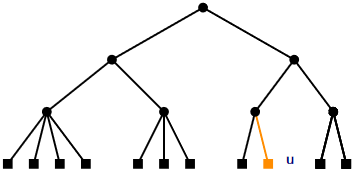
Adding a leaf to a 2-4 tree is easy (see Figure \(\PageIndex{2}\)). If we want to add a leaf \(\mathtt{u}\) as the child of some node \(\mathtt{w}\) on the second-last level, then we simply make \(\mathtt{u}\) a child of \(\mathtt{w}\). This certainly maintains the height property, but could violate the degree property; if \(\mathtt{w}\) had four children prior to adding \(\mathtt{u}\), then \(\mathtt{w}\) now has five children. In this case, we split \(\mathtt{w}\) into two nodes, \(\mathtt{w}\) and \(\mathtt{w}\)', having two and three children, respectively. But now \(\mathtt{w}\)' has no parent, so we recursively make \(\mathtt{w}\)' a child of \(\mathtt{w}\)'s parent. Again, this may cause \(\mathtt{w}\)'s parent to have too many children in which case we split it. This process goes on until we reach a node that has fewer than four children, or until we split the root, \(\mathtt{r}\), into two nodes \(\mathtt{r}\) and \(\mathtt{r'}\). In the latter case, we make a new root that has \(\mathtt{r}\) and \(\mathtt{r'}\) as children. This simultaneously increases the depth of all leaves and so maintains the height property.
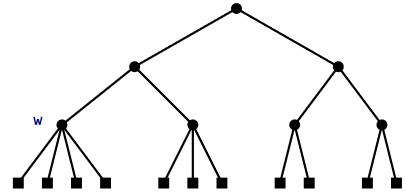
Since the height of the 2-4 tree is never more than \(\log \mathtt{n}\), the process of adding a leaf finishes after at most \(\log \mathtt{n}\) steps.
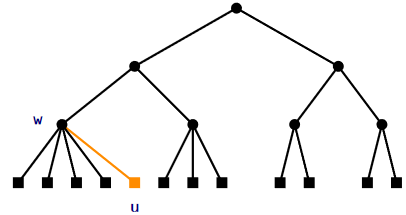
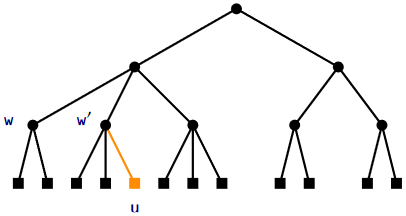
\(\PageIndex{2}\) Removing a Leaf
Removing a leaf from a 2-4 tree is a little more tricky (see Figure \(\PageIndex{3}\)). To remove a leaf \(\mathtt{u}\) from its parent \(\mathtt{w}\), we just remove it. If \(\mathtt{w}\) had only two children prior to the removal of \(\mathtt{u}\), then \(\mathtt{w}\) is left with only one child and violates the degree property.
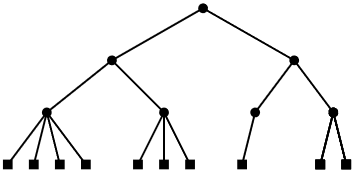
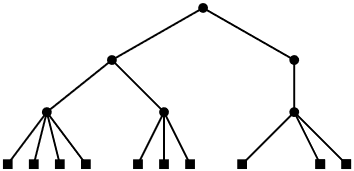
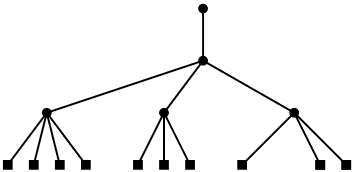
To correct this, we look at \(\mathtt{w}\)'s sibling, \(\mathtt{w'}\). The node \(\mathtt{w'}\) is sure to exist since \(\mathtt{w}\)'s parent had at least two children. If \(\mathtt{w'}\) has three or four children, then we take one of these children from \(\mathtt{w'}\) and give it to \(\mathtt{w}\). Now \(\mathtt{w}\) has two children and \(\mathtt{w'}\) has two or three children and we are done.
On the other hand, if \(\mathtt{w'}\) has only two children, then we merge \(\mathtt{w}\) and \(\mathtt{w'}\) into a single node, \(\mathtt{w}\), that has three children. Next we recursively remove \(\mathtt{w'}\) from the parent of \(\mathtt{w'}\). This process ends when we reach a node, \(\mathtt{u}\), where \(\mathtt{u}\) or its sibling has more than two children, or when we reach the root. In the latter case, if the root is left with only one child, then we delete the root and make its child the new root. Again, this simultaneously decreases the height of every leaf and therefore maintains the height property.
Again, since the height of the tree is never more than \(\log \mathtt{n}\), the process of removing a leaf finishes after at most \(\log \mathtt{n}\) steps.


