5.1: Simple Demultiplexor (UDP)
- Page ID
- 13968
5.1 Simple Demultiplexor (UDP)
5.1 Simple Demultiplexor (UDP)
The simplest possible transport protocol is one that extends the host-to-host delivery service of the underlying network into a process-to-process communication service. There are likely to be many processes running on any given host, so the protocol needs to add a level of demultiplexing, thereby allowing multiple application processes on each host to share the network. Aside from this requirement, the transport protocol adds no other functionality to the best-effort service provided by the underlying network. The Internet's User Datagram Protocol is an example of such a transport protocol.
The only interesting issue in such a protocol is the form of the address used to identify the target process. Although it is possible for processes to directly identify each other with an OS-assigned process id (pid), such an approach is only practical in a closed distributed system in which a single OS runs on all hosts and assigns each process a unique id. A more common approach, and the one used by UDP, is for processes to indirectly identify each other using an abstract locater, usually called a port. The basic idea is for a source process to send a message to a port and for the destination process to receive the message from a port.
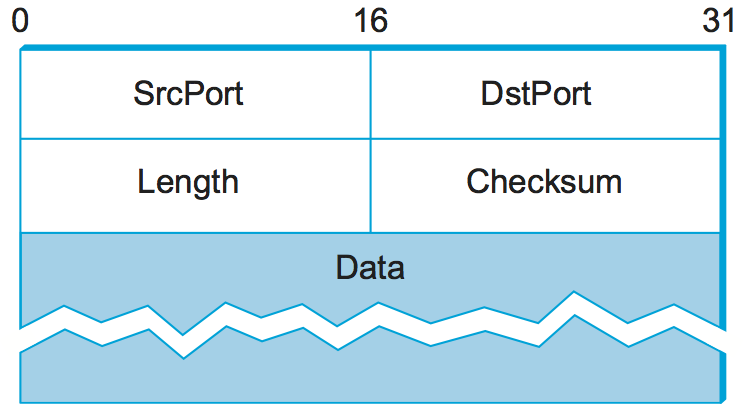
The header for an end-to-end protocol that implements this demultiplexing function typically contains an identifier (port) for both the sender (source) and the receiver (destination) of the message. For example, the UDP header is given in Figure 1. Notice that the UDP port field is only 16 bits long. This means that there are up to 64K possible ports, clearly not enough to identify all the processes on all the hosts in the Internet. Fortunately, ports are not interpreted across the entire Internet, but only on a single host. That is, a process is really identified by a port on some particular host: a (port, host) pair. This pair constitutes the demultiplexing key for the UDP protocol.
The next issue is how a process learns the port for the process to which
it wants to send a message. Typically, a client process initiates a
message exchange with a server process. Once a client has contacted a
server, the server knows the client's port (from the SrcPrt field
contained in the message header) and can reply to it. The real problem,
therefore, is how the client learns the server's port in the first
place. A common approach is for the server to accept messages at a
well-known port. That is, each server receives its messages at some
fixed port that is widely published, much like the emergency telephone
service available in the United States at the well-known phone
number 911. In the Internet, for example, the Domain Name Server (DNS)
receives messages at well-known port 53 on each host, the mail service
listens for messages at port 25, and the Unix talk program accepts
messages at well-known port 517, and so on. This mapping is published
periodically in an RFC and is available on most Unix systems in file
/etc/services. Sometimes a well-known port is just the starting point
for communication: The client and server use the well-known port to
agree on some other port that they will use for subsequent
communication, leaving the well-known port free for other clients.
An alternative strategy is to generalize this idea, so that there is only a single well-known port—the one at which the port mapper service accepts messages. A client would send a message to the port mapper's well-known port asking for the port it should use to talk to the "whatever" service, and the port mapper returns the appropriate port. This strategy makes it easy to change the port associated with different services over time and for each host to use a different port for the same service.
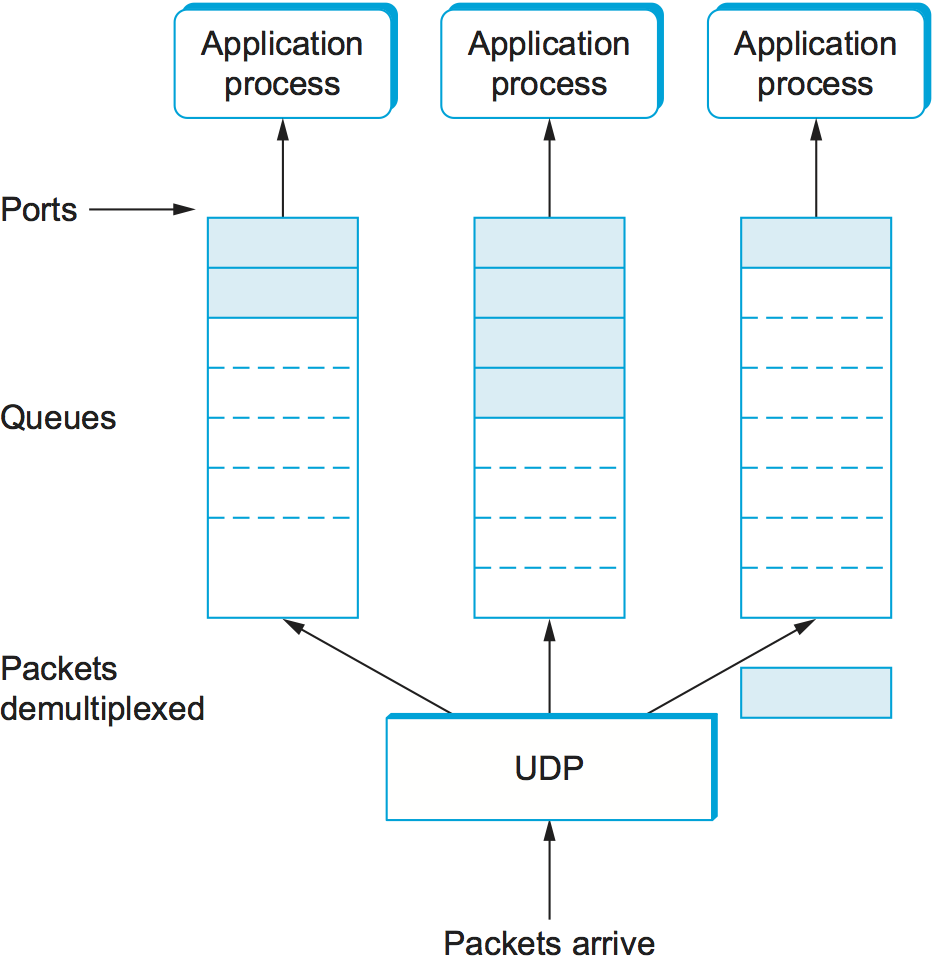
As just mentioned, a port is purely an abstraction. Exactly how it is implemented differs from system to system, or more precisely, from OS to OS. For example, the socket API described in Chapter 1 is an example implementation of ports. Typically, a port is implemented by a message queue, as illustrated in Figure 2. When a message arrives, the protocol (e.g., UDP) appends the message to the end of the queue. Should the queue be full, the message is discarded. There is no flow-control mechanism in UDP to tell the sender to slow down. When an application process wants to receive a message, one is removed from the front of the queue. If the queue is empty, the process blocks until a message becomes available.
Finally, although UDP does not implement flow control or reliable/ordered delivery, it does provide one more function aside from demultiplexing messages to some application process—it also ensures the correctness of the message by the use of a checksum. (The UDP checksum is optional in IPv4 but is mandatory in IPv6.) The basic UDP checksum algorithm is the same one used for IP—that is, it adds up a set of 16-bit words using ones' complement arithmetic and takes the ones' complement of the result. But the input data that is used for the checksum is a little counterintuitive.
The UDP checksum takes as input the UDP header, the contents of the message body, and something called the pseudoheader. The pseudoheader consists of three fields from the IP header—protocol number, source IP address, and destination IP address—plus the UDP length field. (Yes, the UDP length field is included twice in the checksum calculation.) The motivation behind having the pseudoheader is to verify that this message has been delivered between the correct two endpoints. For example, if the destination IP address was modified while the packet was in transit, causing the packet to be misdelivered, this fact would be detected by the UDP checksum.

