5.14: Exercises

Exercise \(\PageIndex{1}\)

The time module provides a function, also named time, that returns the current Greenwich Mean Time in “the epoch”, which is an arbitrary time used as a reference point. On UNIX systems, the epoch is 1 January 1970.

>>> import time
>>> time.time()
1437746094.5735958

Write a script that reads the current time and converts it to a time of day in hours, minutes, and seconds, plus the number of days since the epoch.

Exercise \(\PageIndex{2}\)

Fermat’s Last Theorem says that there are no positive integers a, b, and c such that

\[ a^n + b^n = c^n \nonumber \]

for any values of n greater than 2.

1. Write a function named check_fermat that takes four parameters—a, b, c and n—and checks to see if Fermat’s theorem holds. If n is greater than 2 and

   \[ a^n + b^n = c^n \nonumber \]

   the program should print, “Holy smokes, Fermat was wrong!” Otherwise the program should print, “No, that doesn’t work.”

2. Write a function that prompts the user to input values for a, b, c and n, converts them to integers, and uses check_fermat to check whether they violate Fermat’s theorem.

Exercise \(\PageIndex{3}\)

If you are given three sticks, you may or may not be able to arrange them in a triangle. For example, if one of the sticks is 12 inches long and the other two are one inch long, you will not be able to get the short sticks to meet in the middle. For any three lengths, there is a simple test to see if it is possible to form a triangle:

If any of the three lengths is greater than the sum of the other two, then you cannot form a triangle. Otherwise, you can. (If the sum of two lengths equals the third, they form what is called a “degenerate” triangle.)

1. Write a function named is_triangle that takes three integers as arguments, and that prints either “Yes” or “No”, depending on whether you can or cannot form a triangle from sticks with the given lengths.
2. Write a function that prompts the user to input three stick lengths, converts them to integers, and uses is_triangle to check whether sticks with the given lengths can form a triangle.

Exercise \(\PageIndex{4}\)

What is the output of the following program? Draw a stack diagram that shows the state of the program when it prints the result.

def recurse(n, s):
    if n == 0:
        print(s)
    else:
        recurse(n-1, n+s)

recurse(3, 0)

1. What would happen if you called this function like this: recurse(-1, 0)?
2. Write a docstring that explains everything someone would need to know in order to use this function (and nothing else).

The following exercises use the turtle module, described in Chapter 4:

Exercise \(\PageIndex{5}\)

Read the following function and see if you can figure out what it does (see the examples in Chapter 4). Then run it and see if you got it right.

def draw(t, length, n):
    if n == 0:
        return
    angle = 50
    t.fd(length*n)
    t.lt(angle)
    draw(t, length, n-1)
    t.rt(2*angle)
    draw(t, length, n-1)
    t.lt(angle)
    t.bk(length*n)

Figure \(\PageIndex{1}\): A Koch curve.

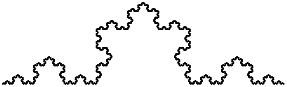
Exercise \(\PageIndex{6}\)

The Koch curve is a fractal that looks something like Figure \(\PageIndex{1}\). To draw a Koch curve with length x, all you have to do is

1. Draw a Koch curve with length x/3.
2. Turn left 60 degrees.
3. Draw a Koch curve with length x/3.
4. Turn right 120 degrees.
5. Draw a Koch curve with length x/3.
6. Turn left 60 degrees.
7. Draw a Koch curve with length x/3.

The exception is if x is less than 3: in that case, you can just draw a straight line with length x.

1. Write a function called koch that takes a turtle and a length as parameters, and that uses the turtle to draw a Koch curve with the given length.
2. Write a function called snowflake that draws three Koch curves to make the outline of a snowflake.

   Solution

   http://thinkpython2.com/code/koch.py

3. The Koch curve can be generalized in several ways. See http://en.Wikipedia.org/wiki/Koch_snowflake for examples and implement your favorite.