1.6: Integer Arithmetic
- Page ID
- 27020
1.6.1 Integer Addition
Binary whole number addition was covered in chapter 1.4. Integer addition is similar to binary whole number addition except that both positive and negative numbers must be considered. For example, consider adding the two positive numbers 00102 (210) + 00112 (310) = 01012 (510).
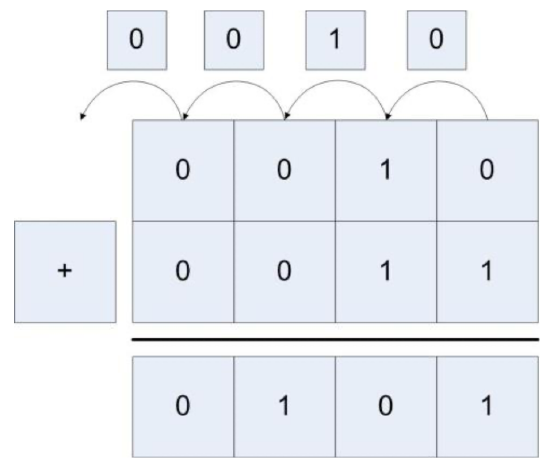
Addition of mixed positive and negative numbers, and two negative numbers also works in the same manner, as the following two examples show. The first adds 00102 (210) + 11012 (-310) = 11112 (-110), and the second adds 11102 (-210) + 11012 (-310) = 10112 (-510).
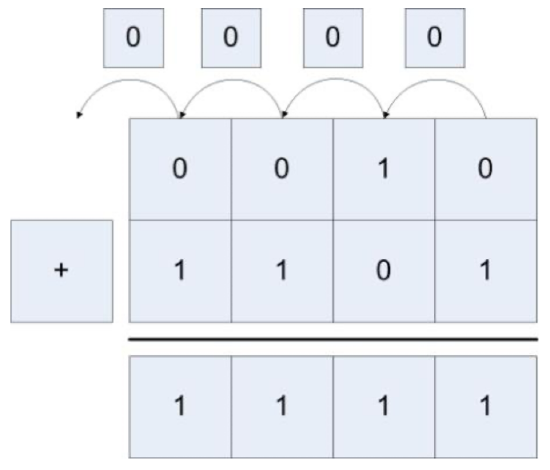
Because integers have fixed sizes, addition and subtraction can cause a problem known as integer overflow. This happens which the two numbers which are being added are large positive or negative values, and the combining of the values results in numbers too big to be store in the integer.
1.6.2 Overflow of Integer Addition
Because integers have fixed sizes, addition and subtraction can cause a problem known as integer overflow. This happens which the two numbers which are being added are large positive or negative values, and the combining of the values results in numbers too big to be store in the integer value.
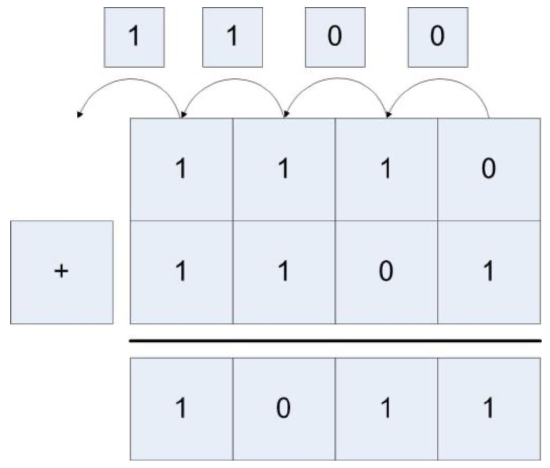
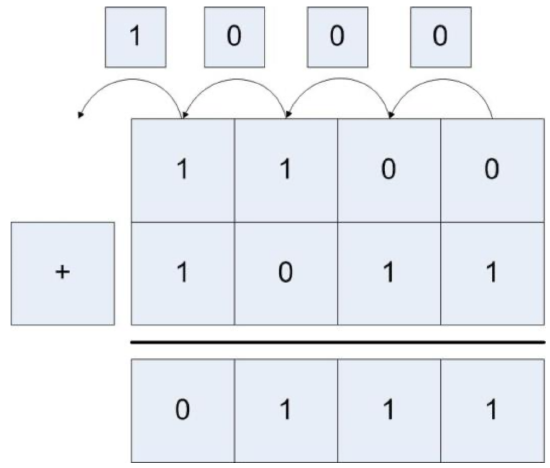
For example, a 4 bit integer can store values from -8...7. So when 01002 (410) + 01012 (5) = 10012 (-7) are added using 4 bit integers the result is too large to store in the integer. When this happens, the number changes sign and gives the wrong answer, as the following figure shows.
Attempting to algorithmically figure out if overflow occur is difficult. First if one number is positive and the other is negative, overflow never occurs. If both numbers are positive or negative, then if the sign of the sum is different than the sign of either of the inputs overflow has occurred.
There is a much easier way to figure out if overflow has occurred. If the carry in bit to the last digit is the same as the carry out bit, then no overflow has occurred. If they are different, then overflow has occurred. In figure 1.3 the carry in and carry out for the last bit are both 0, so there is no overflow. Likewise, in figure 1.4 the carry in and carry out are both 1, so there was no overflow. In figure 1.5 the carry in is 1 and the carry out is 0, so overflow has occurred.
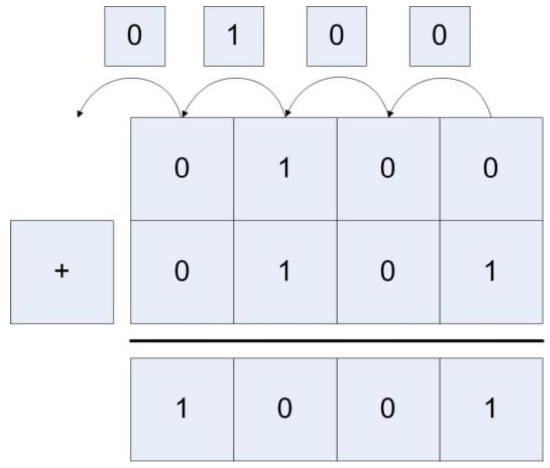
This method also works for addition of negative numbers. Consider adding 11002 (-410) and 10112 (-510) = 01112 (710), shown in figure 1.6. Here the carry in is 0 and the carry out is 1, so once again overflow has occurred.
1.6.3 Integer multiplication using bit shift operations
Multiplication and division of data values or variables involves hardware components in the Arithmetic Logic Unit (ALU). In assembly these operations will be provided by the various forms mul and div operators, and the hardware to implement them is beyond the scope of this book and will not be covered. However, what is of interest in writing assembly is multiplication and division by a constant.
The reason multiplication and division by a constant is covered is that these operations can be provided by bit shift operations, and the bit shift operations are often faster to run than the equivalent mul or div operation. Therefore, bit shift operations are often used in assembly to do multiplication and division, and therefore it is important for assembly language programmers to understand how this works.
First consider multiplication of a number by a power of 10 in base 10. In base 10, if a number is multiplied by a power of 10 (10n , where n is the power of 10), it is sufficient to move the number n places to the right filling in with 0's. For example, 15*1000 (or 15 * 103) = 15,000.
This same concept holds in binary. To multiply a binary number (e.g. 15, or 000011112) by 2, the number is shifted to the left 1 digit (written as 1111<<1), yielding 000111102 or 30. Likewise multiplying 000011112 by 8 is done by moving the number 3 spaces to the left (000011112<<3), yielding 011110002, or 120. So it is easy to multiply any number represented in base 2 by a power of 2 (for example 2n) by doing n left bit shifts and backfilling with 0's.
Note that this also works for multiplication of negative 2's complement (or integer) numbers. Multiplying 111100012 (-15) by 2 is done by moving the bits left 1 space and again appending a 0, yielding 111000102 (or -30) (note that in this case 0 is used for positive or negative numbers). Again multiply 111100012 (-15) by 8 is done using 3 bit shifts and backfilling the number again with zeros, yielding 100010002 (-120)
By applying simple arithmetic, it is easy to see how to do multiplication by a constant 10. Multiplication by 10 can be thought of as multiplication by (8+2), so (n*10) = ((n*8)+(n*2)).
15*10 = 15 * (8+2) = 15 *8 + 15 * 2 = (000011112 << 3) + (000011112 << 1) = 11110002 + 111102 = 1001001102 = 150
This factoring procedure applies for multiplication by any constant, as any constant can be represented by adding powers of 2. Thus any constant multiplication can be encoded in assembly as a series of shifts and adds. This is sometimes faster, and often easier, than doing the math operations, and should be something every assembly language programmer should be familiar with.
This explanation of the constant multiplication trick works in assembly, which begs the question does it also work in a HLL? The answer is yes and no. Bit shifts and addition can be done in most programming languages, so constant multiplication can be implemented as bits shifts and addition. But because it can be done does not mean it should be done. In HLL (C/C++, Java, C#, etc.) this type of code is arcane, and difficult to read and understand. In addition, any decent compiler will convert constant multiplication into the correct underlying bit shifts and additions when it is more efficient to do so. And the compiler will make better decisions about when to use this method of multiplication, and implement it more effectively and with fewer errors than if a programmer were to do it. So unless there is some really good reason to do multiplication using bit shifts and addition, it should be avoided in a HLL.
1.6.4 Integer division using bit shift operations
Since multiplication can be implemented using bit shift operations, the obvious question is whether or not the same principal applies to division? The answer is that for some useful cases, division using bit shift operations does work. But in general, it is full of problems.
The cases where division using bit shift operations works are when the dividend is positive, and the divisor is a power of 2. For example, 000110012 (25) divided by 2 would be a 1-bit shift, or 000011002 (12). The answer 12.5 is truncated, as this is easily implemented by throwing away the bit which has been shifted out. Likewise,00 0110012 (25) divided by 2 is 000000112 (3), with truncation again occurring. Note also that in this case the bit that is shifted in is the sign bit, which is necessary to maintain the correct sign of the number.
Bit shifting for division is useful in some algorithms such as a binary search finding parents in a complete binary tree. But again it should be avoided unless there is a strong reason to use it in a HLL.
This leaves two issues. The first is why can this method not be implemented with constants other than the powers of 2. The reason is that division is only distributive in one direction over addition, and in our case it is the wrong direction. Consider the equation 60/10. It is easy to show that division over addition does not work in this case.
60/10 = 60/(8+2) ≠ 60/8 + 60/2
The second issue is why the dividend must be positive. To see why this is true, consider the following division, -15 / 2. This result in the following:
111110012 >> 1 = 11111100 = -8
Two things about this answer. First in this case the sign bit, 1, must be shifted in to maintain the sign of the integer.
Second in this case the lowest bit, a 1, is truncated. This means that -7.5 is truncated down to -8. However, many programmers believe that -7.5 should truncate to -7. Whether the correct answer is -7 or -8 is debatable, and different programming languages have implemented as either value (for example, Java implements -15/2 = -7, but Python -15/2 as -8). This same problem occurs with many operations on negative numbers, such a modulus. And while such debates might be fun, and programmers should realize that these issues can occur, it is not the purpose of this book to do more than present the problem.


