8.1: Stacks

This section will cover the concept of a program stack. To do so, first the data structure of a stack will be implemented.

8.1.1 Stack data structure: definition

Many readers will come into the material in this chapter with either no understanding, or a poor understanding, of a stack data structure. It therefore makes sense to include a section on what a stack is, and how it works.

A stack is a Last-In-First-Out data structure. The most commonly used metaphor for a stack in a computer is trays in a lunch room. When a tray is returned to the stack, it is placed on top of the stack, and each subsequent tray placed on top of the previous tray. When a patron wants a try, they take the first one off of the top of the tray stack. Hence the last tray returned is the first try used. To better understand this, note that some trays will be heavily used (those on the top), and some, such as the bottom most tray, might never be used.

In a computer a stack is implemented as an array on which there are two operations, push and pop. The push operation places an item on the top of the stack, and so places the item at the next available spot in the array and adds 1 to a array index to the next available spot. A pop operation removes the top most item, so returns the item on top of stack, and subtracts 1 from the size of the stack.

The following is an example of how a stack works. The example begins by creating a data structure for a stack, which is shown below. Note that there is no error checking.

Program 8-1: Stack class definition

class Stack
{
    int SIZE=100;
    int[SIZE] elements;
    int last = 0;
    push(int newElement)
    {
        elements[last] = newElement;
        last = last + 1
    }
    int pop()
    {
        last = last - 1;
        return element[last];
    }
}

To see how the array works, the following example illustrates the following operations:

push(5)
push(7)
push(2)
print(pop())
push(4)
print(pop())
print(pop())

Figure 8-1: Push/Pop Example 1

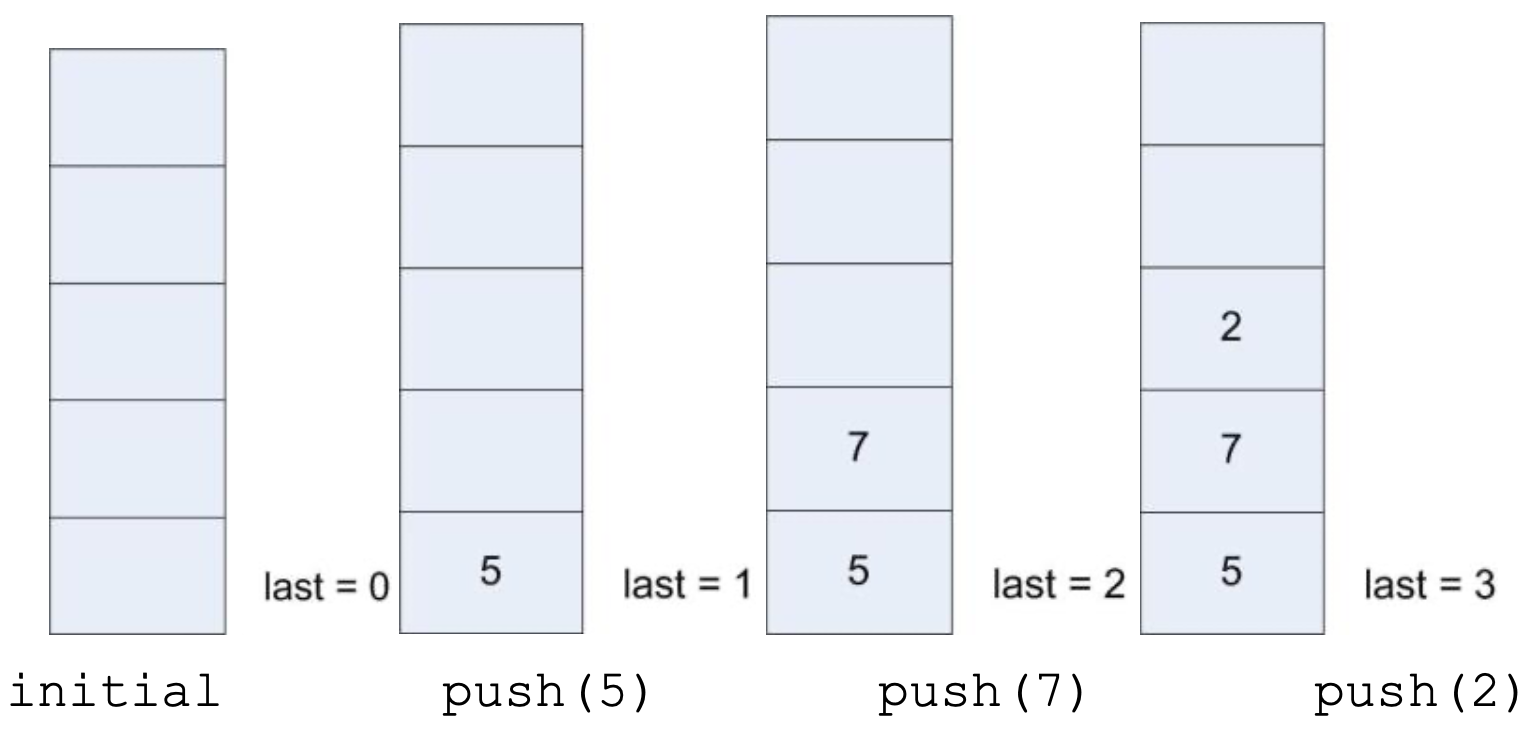
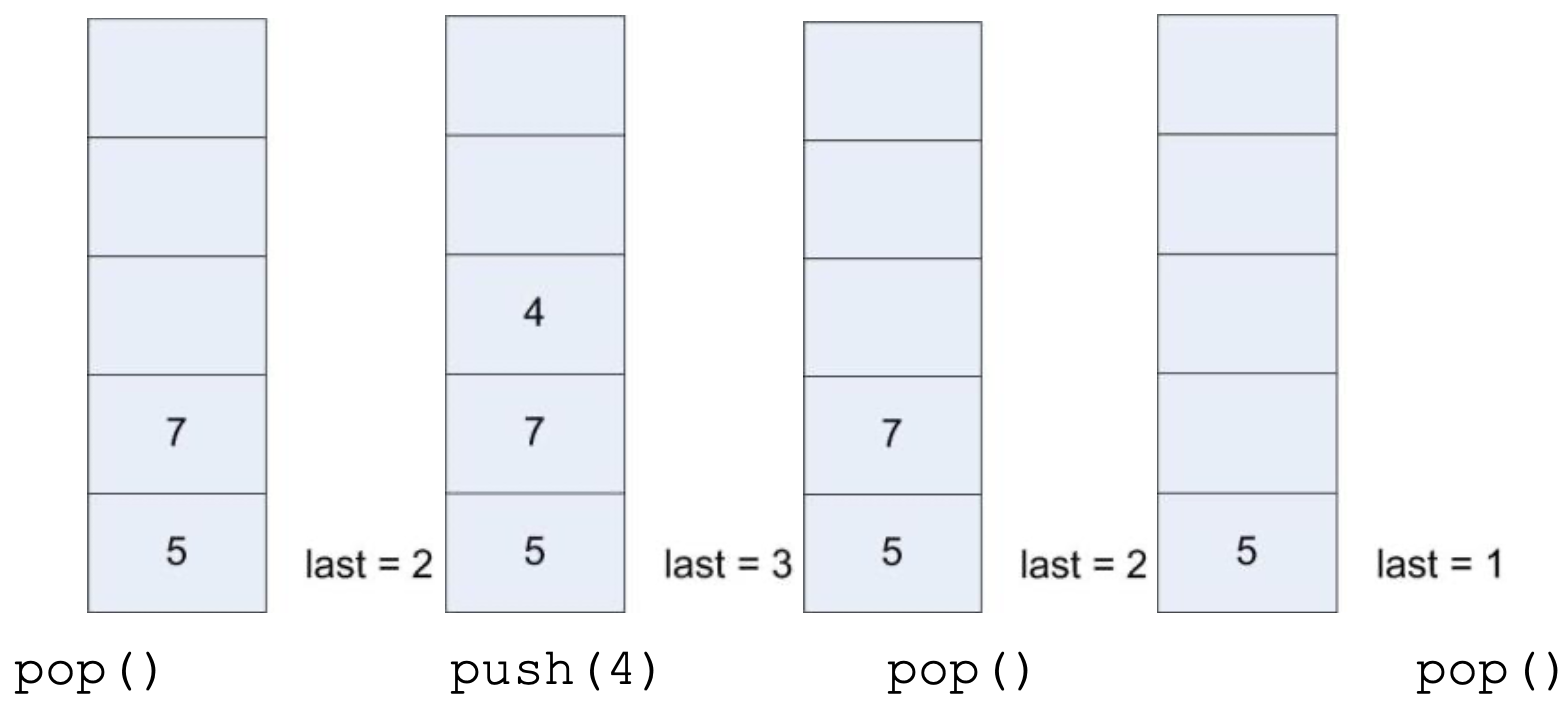
The output of the program would be 2, 4, 7.

8.1.2 Another stack implementation

The stack of tray metaphor used in the previous section has the same problem as all metaphors and analogies, that is you cannot reason about the underlying problem using a metaphor or analogy. Of all the logic errors that exist in the world, this is probably the most common, and the most harmful.

For example, there is another stack implementation that is better suited to our needs in describing the program stack. This stack implementation is still a LIFO data structure, but it will grow down in memory and the items on it will not be fixed sized. This is completely alien to our cafeteria tray metaphor, so this text will abandon that metaphor as quickly as it introduced it.

In this implementation, the stack will store groups of characters (strings) of varying sizes. The storage for the stack will use an array of size 7 of elements. Each character will be stored in an element. Because the stack grows downward in memory, the first item in the string will be allocated at elements[size-1], and each time a new string is desired, it will be stored in the next lowest available place in memory. Because the strings are not all the same size, the size of each string must be stored in the array with the characters. This means that with each string a number must be stored which gives the size of the string.

In the above paragraph, it says that the strings are not all the same size, but it purposefully does not say that the strings are not all fixed size. The strings must have a known, fixed size when the push operation is executed. This is an important point which will have an impact when discussing the program stack.

The data structure for this new stringStack class is defined below.

Program 8-2: String class stack definition

class stringStack
{
    int SIZE=7;
    int elements[SIZE]; # Note that characters are stored as int    
    int last = SIZE-1;
    push(String s) {
        last = (last - s.length())-1;
        elements[last] = s.length();
        int i = last + 1;
        for (char c in s)
        {
            elements[i] = c;
            i = i + 1;
        }    
    }
    
    String pop()
    {
        int i = elements[last];
        int j = last + 1;
        last = last + i;
        for ( ; j < last; j++) {
            s = s + elements[j];
        }
        return s;
    }
}                

Note that in the StringStack class the size of the string is stored with the string on the stack, and the push and pop operations use the size to determine the amount of memory to be allocated/deallocated. The following illustrates this stack after the strings “ab” and “cde” have been pushed on the stack.