4.5: Subdecks
- Page ID
- 15295
The first step of merge sort is to split the deck into two subdecks, each with about half the cards. So we might want a method, subdeck, that takes a deck and a range of indexes. It returns a new deck that contains the specified subset of the cards:
public Deck subdeck(int low, int high) {
Deck sub = new Deck(high - low + 1);
for (int i = 0; i < sub.cards.length; i++) {
sub.cards[i] = this.cards[low + i];
}
return sub;
}
The first line creates an unpopulated subdeck. Inside the for loop, the subdeck gets populated with copies of references from the deck.
The length of the subdeck is high - low + 1, because both the low card and the high card are included. This sort of computation can be confusing, and forgetting the + 1 often leads to “off-by-one” errors. Drawing a picture is usually the best way to avoid them.
Figure 13.5.1 is a state diagram of a subdeck with low = 0 and high = 4. The result is a hand with five cards that are shared with the original deck; that is, they are aliased.
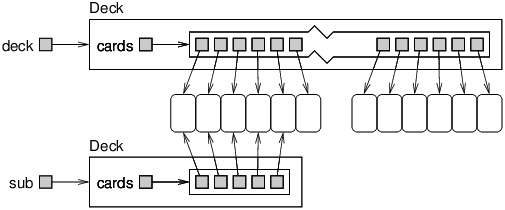
subdeck.Aliasing might not be a good idea, because changes to shared cards would be reflected in multiple decks. But since Card objects are immutable, this kind of aliasing is not a problem at all.


