2.3: Mathematical Proof
- Page ID
- 9673
Understandably, mathematicians are very picky about getting their proofs right. It’s how they construct their world. Students sometimes object that mathematicians are too picky about proving things that are ‘obvious’. But the fact that something is obvious in the real world counts for very little in the constructed world of mathematics. Too many obvious things have turned out to be dead wrong. (For that matter, even things in the real world that seem ‘obviously’ true are not necessarily true at all.)
For example, consider the quantity f (n) = n2 + n + 41. When n = 0,f(n) = 41 which is prime; when n = 1, f(n) = 43 which is prime; when n = 2, f (n) = 47, which is prime. By the time you had calculatedf (3), f (4), . . . , f (10) and found that they were all prime, you might conclude that it is ‘obvious’ that f (n) is prime for all n ≥ 0. But this is not in fact the
case! (See exercises.)
As we saw in Section 2.5, a formal proof consists of a sequence of statements where each statement is either an assumption or follows by a rule of logic from previous statements. The examples in that section all worked with unspecified generic propositions (p, q, etc). Let us now look at how one might use the same techniques to prove a specific proposition about the mathematical world. We will prove that for all integers n, if n is even then n2 is even. (Definition: an integer n is even iff n = 2k for some integer k. For example, 2 is even since 2 = 2 · 1; 66 is even since 66 = 2 · 33; 0 is even since 0 = 2 · 0.)
Proof. This is a proposition of the form ∀n(P(n) → Q(n)) where P(n) is “n is even” andQ(n) is “n2 is even.” We need to show that P(n) → Q(n) is true for all values of n. Or alternatively we can phrase it as: ∀n(E(n) → E(n2)) where E(x) is ‘x is even’.
In the language of Section 2.5, we need to show that for any n, E(n) logically implies E(n2); or, equivalently, that E\(\left(n^{2}\right)\) can be logically deduced from E(n); or, equivalently, that
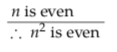
is a valid argument. Here is a formal proof that
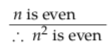
is in fact a valid argument for any value of n:
Let n be an arbitrary integer.

(The “basic fact about integers” referred to above is that the product of integers is again an integer.) Since n could be replaced by any integer throughout this argument, we have proved the statement “if n is even then n2 is even” is true for all integers n. (You might worry that the argument is only valid for even n; see the disclaimer about Feyenoord’s football ability on page 47, or remind yourself that P(n) → Q(n) is automatically true ifP(n) is false.)
Mathematical proofs are rarely presented with this degree of detail and formality. A slightly less formal proof of our proposition might leave out the explicit implications and instances of modus ponens and appear as follows:
Proof. Let n be an arbitrary integer.

Since n was an arbitrary integer, the statement is true for all integers.
A more typical proof would take the argument above and present it in prose rather
than list form:
Proof. Let n be an arbitrary integer and assume n is even. Then n = 2k for some integerk by the definition of even, and n2 = 4k2 = 2(2k2). Since the product of integers is an integer, we have n2 = 2k′ for some integer k′. Therefore n2 is even. Since n was an arbitrary integer, the statement is true for all integers.
Typically, in a ‘formal’ proof, it is this kind of (relatively) informal discussion that is given, with enough details to convince the reader that a complete, formal proof could be constructed. Of course, how many details the reader can be expected to fill in depends on the reader, and reading proofs is a skill that must be developed and practiced.
In the course Reasoning & Logic you are learning to write proper formal proofs, and as a part of that we also need to evaluate your performance. To this end we ask you to write proofs similar to the second example given above (the list form rather than the prose form) as this shows more clearly that you are aware of the formalisms required in a proof.
Writing a proof is even more difficult. Every proof involves a creative act of discovery, in which a chain of logic that leads from assumptions to conclusion is discovered. It also involves a creative act of expression, in which that logic is presented in a clear and convincing way. There is no algorithm for producing correct, coherent proofs. There are, however, some general guidelines for discovering and writing proofs. Let’s look at some of these next.


