3.2.1: Set Complement
- Page ID
- 10576
While ∪ is analogous to ∨ and ∩ is analogous to ∧, we have not yet seen any operation in set theory that is analogous to the logical ‘not’ operator, ¬. Given a set A, it is tempting to try to define {x | ¬(x ∈ A)}, the set that contains everything that does not belong to A. Unfortunately, the rules of set theory do not allow us to define such a set. The notation{x | P(x)} can only be used when the domain of discourse of P is a set, so there must be an underlying set from which the elements that are/are not in A are chosen, i.e., some underlying set of which A is a subset. We can get around this problem by restricting the discussion to subsets of some fixed set. This set will be known as the universal set. Keep in mind that the universal set is only universal for some particular discussion. It is simply some set that is large enough to contain all the sets under discussion as subsets. Given a universal set U and any subset A of U, we can define the set {x ∈ U | ¬(x ∈ A)}.
Definition 4.1.
Let U be a given universal set, and let A be any subset of U. We define the complement of A in U to be the set \(\overline{A}\) that is defined by \(\overline{A}=\{x \in U | x \notin A\}\).
Usually, we will refer to the complement of A in U simply as the complement of A, but you should remember that whenever complements of sets are used, there must be some universal set in the background. Other textbooks may use \(A^{c}\) to denote the complement of A instead.
Given the complement operation on sets, we can look for analogues to the rules of 4 logic that involve negation. For example, we know that p ∧ ¬p = F for any proposition p. It follows that for any subset A of U,
\(A \cap \overline{A}=\{x \in U |(x \in A) \wedge(x \in \overline{A})\}\) (definition of ∩)
\(=\{x \in U |(x \in A) \wedge(x \notin A)\}\) (definition of complement)
\(=\{x \in U |(x \in A) \wedge \neg(x \in A)\}\) (definition of \(\not \notin )\)
=∅
the last equality following because the proposition (x ∈ A) ∧ ¬(x ∈ A) is false for any \(x .\) Similarly, we can show that \(A \cup \overline{A}=U\) and that \(\overline{\overline{A}}=A\) (where \(\overline{\overline{A}}\)) is the complement of the complement of \(A,\) that is, the set obtained by taking the complement of \(\vec{A} .\) .
The most important laws for working with complements of sets are DeMorgan’s Laws for sets. These laws, which follow directly from DeMorgan’s Laws for logic, state that for any subsets A and B of a universal set U,
\(\overline{A \cup B}=\overline{A} \cap \overline{B}\)
and
\(\overline{A \cap B}=\overline{A} \cup \overline{B}\)
For example, we can verify the first of these laws with the calculation
\(\overline{A \cup B}=\{x \in U | x \notin(A \cup B)\}\) (definition of complement)
= {x ∈ U | ¬(x ∈ A ∪ B)} (definition of \(\notin )\)
= {x ∈ U | ¬(x ∈ A ∨ x ∈ B)} (definition of ∪)
= {x ∈ U|(¬(x ∈ A))∧(¬(x ∈ B))} (DeMorgan’s Law for logic)
= {x ∈ U | (x ) ∧ (x )} (definition of \(\notin )\)
\(=\{x \in U |(x \in \overline{A}) \wedge(x \in \overline{B})\}\) (definition of complement)
\(=\overline{A} \cap \overline{B}\) (definition of ∩)
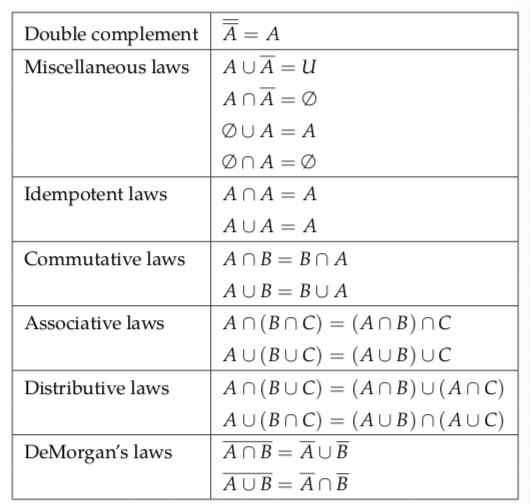
Figure 4.4: Some Laws of Boolean Algebra for sets. A, B, and C are sets. For the laws that involve the complement operator, they are assumed to be subsets of some universal set, U. For the most part, these laws correspond directly to laws of Boolean Algebra for propositional logic as given in Figure 2.2.
An easy inductive proof can be used to verify generalized versions of DeMorgan’s Laws for set theory. (In this context, all sets are assumed to be subsets of some unnamed universal set.) A simple calculation verifies DeMorgan’s Law for three sets:
\(\overline{A \cup B \cup C}=\overline{(A \cup B) \cup C}\)
\(=\overline{(A \cup B)} \cap \overline{C}\) (by DeMorgan’s Law for two sets)
\(=(\overline{A} \cap \overline{B}) \cap \overline{C}\) (by DeMorgan’s Law for two sets)
\(=\overline{A} \cap \overline{B} \cap \overline{C}\)
From there, we can derive similar laws for four sets, five sets, and so on. However, just saying ‘and so on’ is not a rigorous proof of this fact. Whereas we may have excused ourselves about that in Chapter 2, we can now prove this fact. Here is a rigorous inductive proof of a generalized DeMorgan’s Law:
Theorem 4.5.
For any natural number \(n \geq 2\) and for any sets \(X_{1}, X_{2}, \ldots, X_{n}\)
\(\overline{X_{1} \cup X_{2} \cup \cdots \cup X_{n}}=\overline{X_{1}} \cap \overline{X_{2}} \cap \cdots \cap \overline{X_{2}}\)
Proof. We give a proof by induction. In the base case, n = 2, the statement is that \(\overline{X_{1} \cup X_{2}}\)\(=\overline{X_{1}}\)\(\cap\)\(=\overline{X_{n}}\) This is true since it is just an application of DeMorgan’s law for two sets.
For the inductive case, suppose that the statement is true for n = k. We want to show that it is true for \(n=k+1 .\) Let \(X_{1}, X_{2}, \ldots, X_{k+1}\) be any \(k+1\) sets. Then we have:
\(\overline{X_{1} \cup X_{2} \cup \cdots \cup X_{k+1}}=\overline{\left(X_{1} \cup X_{2} \cup \cdots \cup X_{k}\right) \cup X_{k+1}}\)
\(=\overline{\left(X_{1} \cup X_{2} \cup \cdots \cup X_{k}\right)} \cap \overline{X_{k+1}}\)
\(=\left(\overline{X_{1}} \cap \overline{X_{2}} \cap \cdots \cap \overline{X_{k}}\right) \cap \overline{X_{k+1}}\)
\(=\overline{X_{1}} \cap \overline{X_{2}} \cap \cdots \cap \overline{X_{k+1}}\)
In this computation, the second step follows by DeMorgan’s Law for two sets, while the third step follows from the induction hypothesis. Therefore by the principle of induction we have proven the theorem.

