5.1: Ordinary Induction

To understand how induction works, suppose there is a professor who brings a bottomless bag of assorted miniature candy bars to her large class. She offers to share the candy in the following way. First, she lines the students up in order. Next she states two rules:

1. The student at the beginning of the line gets a candy bar.
2. If a student gets a candy bar, then the following student in line also gets a candy bar.

Let’s number the students by their order in line, starting the count with 0, as usual in computer science. Now we can understand the second rule as a short description of a whole sequence of statements:

• If student 0 gets a candy bar, then student 1 also gets one.
• If student 1 gets a candy bar, then student 2 also gets one.
• If student 2 gets a candy bar, then student 3 also gets one.

:

Of course, this sequence has a more concise mathematical description:

If student \(n\) gets a candy bar, then student \(n + 1\) gets a candy bar, for all nonnegative integers \(n\).

So suppose you are student 17. By these rules, are you entitled to a miniature candy bar? Well, student 0 gets a candy bar by the first rule. Therefore, by the second rule, student 1 also gets one, which means student 2 gets one, which means student 3 gets one as well, and so on. By 17 applications of the professor’s second rule, you get your candy bar! Of course the rules really guarantee a candy bar to every student, no matter how far back in line they may be.

A Rule for Ordinary Induction

The reasoning that led us to conclude that every student gets a candy bar is essentially all there is to induction.

The Induction Principle.

Let \(P\) be a predicate on nonnegative integers. If

• \(P(0)\) is true, and
• \(P(n) \text{ IMPLIES } P(n + 1)\) for all nonnegative integers, \(n\),

then

• \(P(m)\) is true for all nonnegative integers, \(m\).

Since we’re going to consider several useful variants of induction in later sections, we’ll refer to the induction method described above as ordinary induction when we need to distinguish it. Formulated as a proof rule as in Section 1.4.1, this would be

Rule. Induction Rule

\[\nonumber \frac{P(0), \quad \forall n \in \mathbb{N} . P(n) \text { IMPLIES } P(n+1)}{\forall m \in \mathbb{N} . P(m)}\]

This Induction Rule works for the same intuitive reason that all the students get candy bars, and we hope the explanation using candy bars makes it clear why the soundness of ordinary induction can be taken for granted. In fact, the rule is so obvious that it’s hard to see what more basic principle could be used to justify it.¹ What’s not so obvious is how much mileage we get by using it.

A Familiar Example

Below is the formula (\ref{5.1.1}) for the sum of the nonnegative integers up to \(n\). The formula holds for all nonnegative integers, so it is the kind of statement to which induction applies directly. We’ve already proved this formula using the Well Ordering Principle (Theorem 2.2.1), but now we’ll prove it by induction, that is, using the Induction Principle.

Theorem \(\PageIndex{1}\)

For all \(n \in \mathbb{N}\),

\[\label{5.1.1} 1+2+3+\cdots+n=\frac{n(n+1)}{2}\]

To prove the theorem by induction, define predicate \(P(n)\) to be the equation (\ref{5.1.1}). Now the theorem can be restated as the claim that \(P(n)\) is true for all \(n \in \mathbb{N}\). This is great, because the Induction Principle lets us reach precisely that conclusion, provided we establish two simpler facts:

• \(P(0)\) is true.
• For all \(n \in \mathbb{N}, P(n) \text { IMPLIES } P(n+1)\).

So now our job is reduced to proving these two statements.

The first statement follows because of the convention that a sum of zero terms is equal to 0. So \(P(0)\) is the true assertion that a sum of zero terms is equal to 0(0+1) / 2=0.

The second statement is more complicated. But remember the basic plan from Section 1.5 for proving the validity of any implication: assume the statement on the left and then prove the statement on the right. In this case, we assume \(P(n)\)— namely, equation (\ref{5.1.1})—in order to prove \(P(n + 1)\), which is the equation

\[\label{5.1.2} 1+2+3+\cdots+n+(n+1)=\frac{(n+1)(n+2)}{2}\]

These two equations are quite similar; in fact, adding \((n + 1)\) to both sides of equation (\ref{5.1.1}) and simplifying the right side gives the equation (\ref{5.1.2}):

\[\begin{aligned}
1+2+3+\cdots+n+(n+1) &=\frac{n(n+1)}{2}+(n+1) \\
&=\frac{(n+2)(n+1)}{2}
\end{aligned}\]

Thus, if \(P(n)\) is true, then so is \(P(n + 1)\). This argument is valid for every nonnegative integer \(n\), so this establishes the second fact required by the induction proof. Therefore, the Induction Principle says that the predicate \(P(m)\) is true for all nonnegative integers, \(m\). The theorem is proved.

A Template for Induction Proofs

The proof of equation (\ref{5.1.1}) was relatively simple, but even the most complicated induction proof follows exactly the same template. There are five components:

1. State that the proof uses induction. This immediately conveys the overall structure of the proof, which helps your reader follow your argument.
2. Define an appropriate predicate The predicate \(P(n)\) is called the induction hypothesis. The eventual conclusion of the induction argument will be that \(P(n)\) is true for all nonnegative \(n\). A clearly stated induction hypothesis is often the most important part of an induction proof, and its omission is the largest source of confused proofs by students. In the simplest cases, the induction hypothesis can be lifted straight from the proposition you are trying to prove, as we did with equation (\ref{5.1.1}). Sometimes the induction hypothesis will involve several variables, in which case you should indicate which variable serves as \(n\).
3. Prove that \(P(0)\) is true. This is usually easy, as in the example above. This part of the proof is called the base case or basis step.
4. Prove that \(P(n)\) implies \(P(n + 1)\) for every nonnegative integer \(n\). This is called the inductive step. The basic plan is always the same: assume that \(P(n)\) is true and then use this assumption to prove that \(P(n + 1)\) is true. These two statements should be fairly similar, but bridging the gap may require some ingenuity. Whatever argument you give must be valid for every nonnegative integer \(n\), since the goal is to prove that all the following implications are true:

\[\nonumber P(0) \rightarrow P(1), P(1) \rightarrow P(2), P(2) \rightarrow P(3), \ldots\]

5. Invoke induction. Given these facts, the induction principle allows you to conclude that \(P(n)\) is true for all nonnegative \(n\). This is the logical capstone to the whole argument, but it is so standard that it’s usual not to mention it explicitly

Always be sure to explicitly label the base case and the inductive step. Doing so will make your proofs clearer and will decrease the chance that you forget a key step—like checking the base case.

A Clean Writeup

The proof of Theorem 5.1.1 given above is perfectly valid; however, it contains a lot of extraneous explanation that you won’t usually see in induction proofs. The writeup below is closer to what you might see in print and should be prepared to produce yourself.

Revised proof of Theorem 5.1.1. We use induction. The induction hypothesis, \(P(n)\), will be equation (\ref{5.1.1}).

Base case: \(P(0)\) is true, because both sides of equation (\ref{5.1.1}) equal zero when \(n = 0\).

Inductive step: Assume that \(P(n)\) is true, that is equation (\ref{5.1.1}) holds for some nonnegative integer \(n\). Then adding \(n + 1\) to both sides of the equation implies that

\[\begin{aligned}
1+2+3+\cdots + n+(n+1) &=\frac{n(n+1)}{2}+(n+1) \\
&=\frac{(n+1)(n+2)}{2} \quad \text { (by simple algebra) }
\end{aligned}\]

which proves \(P(n+1)\).

So it follows by induction that \(P(n)\) is true for all nonnegative \(n\).\(\quad \blacksquare\)

It probably bothers you that induction led to a proof of this summation formula but did not provide an intuitive way to understand it nor did it explain where the formula came from in the first place.² This is both a weakness and a strength. It is a weakness when a proof does not provide insight. But it is a strength that a proof can provide a reader with a reliable guarantee of correctness without requiring insight.

A More Challenging Example

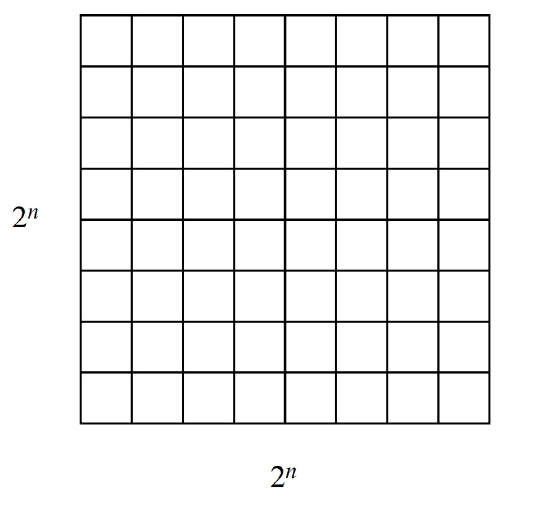
During the development of MIT’s famous Stata Center, as costs rose further and further beyond budget, some radical fundraising ideas were proposed. One rumored plan was to install a big square courtyard divided into unit squares. The big square would be \(2^n\) units on a side for some undetermined nonnegative integer \(n\), and one of the unit squares in the center³ occupied by a statue of a wealthy potential donor—whom the fund raisers privately referred to as “Bill.” The \(n = 3\) case is shown in Figure 5.1.

Figure 5.1 A \(2^n \times 2^n\) courtyard for \(n = 3\).

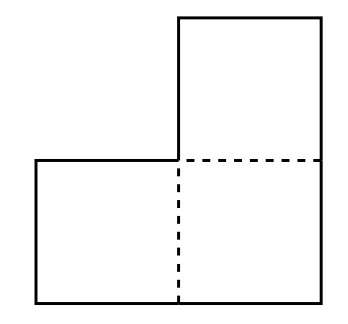
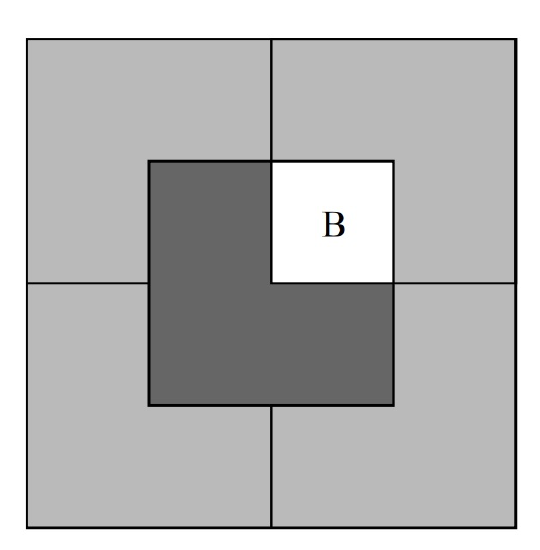
A complication was that the building’s unconventional architect, Frank Gehry, was alleged to require that only special L-shaped tiles (shown in Figure 5.2) be used for the courtyard. For \(n = 2\), a courtyard meeting these constraints is shown in Figure 5.3. But what about for larger values of \(n\)? Is there a way to tile a \(2^n \times 2^n\) courtyard with L-shaped tiles around a statue in the center? Let’s try to prove that this is so.

Figure 5.2 The special L-shaped tile.

Figure 5.3 A tiling using L-shaped tiles for \(n = 2\) with Bill in a center square.

Theorem \(\PageIndex{2}\)

For all \(n \geq 0\) there exists a tiling of a \(2^n \times 2^n\) courtyard with Bill in a central square.

Proof

(doomed attempt) The proof is by induction. Let \(P(n)\) be the proposition that there exists a tiling of a \(2^n \times 2^n\) courtyard with Bill in the center.

Base case: \(P(0)\) is true because Bill fills the whole courtyard.

Inductive step: Assume that there is a tiling of a \(2^n \times 2^n\) courtyard with Bill in the center for some \(n \geq 0\). We must prove that there is a way to tile a \(2^{n+1} \times 2^{n+1}\) courtyard with Bill in the center ...\(\quad \blacksquare\)

Now we’re in trouble! The ability to tile a smaller courtyard with Bill in the center isn’t much help in tiling a larger courtyard with Bill in the center. We haven’t figured out how to bridge the gap between \(P(n)\) and \(P(n+1)\).

So if we’re going to prove Theorem 5.1.2 by induction, we’re going to need some other induction hypothesis than simply the statement about n that we’re trying to prove.

When this happens, your first fallback should be to look for a stronger induction hypothesis; that is, one which implies your previous hypothesis. For example, we could make \(P(n)\) the proposition that for every location of Bill in a \(2^n \times 2^n\) courtyard, there exists a tiling of the remainder.

This advice may sound bizarre: “If you can’t prove something, try to prove something grander!” But for induction arguments, this makes sense. In the inductive step, where you have to prove \(P(n) \text{ IMPLIES } P(n+1)\), you’re in better shape because you can assume \(P(n)\), which is now a more powerful statement. Let’s see how this plays out in the case of courtyard tiling.

Proof (successful attempt). The proof is by induction. Let \(P(n)\) be the proposition that for every location of Bill in a \(2^n \times 2^n\) courtyard, there exists a tiling of the remainder.

Base case: \(P(0)\) is true because Bill fills the whole courtyard.

Inductive step: Assume that \(P(n)\) is true for some \(n \geq 0\); that is, for every location of Bill in a \(2^n \times 2^n\) courtyard, there exists a tiling of the remainder. Divide the (2^{n+1} \times 2^{n+1}\) courtyard into four quadrants, each \(2^n \times 2^n\). One quadrant contains Bill (B in the diagram below). Place a temporary Bill (X in the diagram) in each of the three central squares lying outside this quadrant as shown in Figure 5.4.

Figure 5.4 Using a stronger inductive hypothesis to prove Theorem 5.1.2.

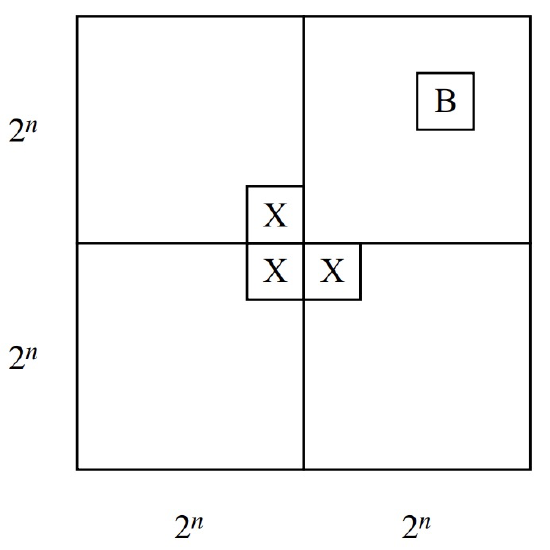
Now we can tile each of the four quadrants by the induction assumption. Replacing the three temporary Bills with a single L-shaped tile completes the job. This proves that \(P(n)\) implies \(P(n+1)\) for all \(n \geq 0\). Thus \(P(n)\) is true for all \(m \in \mathbb{N}\), and the theorem follows as a special case where we put Bill in a central square. \(\quad \blacksquare\)

This proof has two nice properties. First, not only does the argument guarantee that a tiling exists, but also it gives an algorithm for finding such a tiling. Second, we have a stronger result: if Bill wanted a statue on the edge of the courtyard, away from the pigeons, we could accommodate him!

Strengthening the induction hypothesis is often a good move when an induction proof won’t go through. But keep in mind that the stronger assertion must actually be true; otherwise, there isn’t much hope of constructing a valid proof. Sometimes finding just the right induction hypothesis requires trial, error, and insight. For example, mathematicians spent almost twenty years trying to prove or disprove the conjecture that every planar graph is 5-choosable.⁴ Then, in 1994, Carsten Thomassen gave an induction proof simple enough to explain on a napkin. The key turned out to be finding an extremely clever induction hypothesis; with that in hand, completing the argument was easy!

A Faulty Induction Proof

If we have done a good job in writing this text, right about now you should be thinking, “Hey, this induction stuff isn’t so hard after all—just show \(P(0)\) is true and that \(P(n)\) implies \(P(n+1)\) for any number \(n\).” And, you would be right, although sometimes when you start doing induction proofs on your own, you can run into trouble. For example, we will now use induction to “prove” that all horses are the same color—just when you thought it was safe to skip class and work on your robot program instead. Sorry!

False Theorem. All horses are the same color.

Notice that no \(n\) is mentioned in this assertion, so we’re going to have to reformulate it in a way that makes an n explicit. In particular, we’ll (falsely) prove that

False Theorem 5.1.3. In every set of \(n \geq 1\) horses, all the horses are the same color.

This is a statement about all integers \(n \geq 1\) rather \(\geq 0\), so it’s natural to use a slight variation on induction: prove \(P(1)\) in the base case and then prove that \(P(n)\) implies \(P(n+1)\) for all \(n \geq 1\) in the inductive step. This is a perfectly valid variant of induction and is not the problem with the proof below.

Bogus proof. The proof is by induction on \(n\). The induction hypothesis, \(P(n)\), will be

\[\label{5.1.3} \text{In every set of } n \text{ horses, all are the same color.}\]

Base case: \(n = 1\). \(P(1)\) is true, because in a size-1 set of horses, there’s only one horse, and this horse is definitely the same color as itself.

Inductive step: Assume that \(P(n)\) is true for some \(n \geq 1\). That is, assume that in every set of \(n\) horses, all are the same color. Now suppose we have a set of \(n+1\) horses:

\[\nonumber h_{1}, h_{2}, \ldots, h_{n}, h_{n+1}\]

We need to prove these \(n+1\) horses are all the same color.

By our assumption, the first n horses are the same color:

\[\nonumber \underbrace{h_{1}, h_{2}, \ldots, h_{n}}_{\text {same color }}, h_{n+1}\]

Also by our assumption, the last n horses are the same color:

\[\nonumber h_{1}, \underbrace{h_{2}, \ldots, h_{n}, h_{n+1}}_{\text {same color }}\]

So \(h_1\) is the same color as the remaining horses besides \(h_{n+1}\) —that is,\(h_2, \ldots, h_n\). Likewise, \(h_{n+1}\) is the same color as the remaining horses besides \(h_1\)—that is, \(h_2, \ldots, h_n\), again. Since \(h_1\) and \(h_{n+1}\) are the same color as \(h_2, \ldots, h_n\), all \(n + 1\) horses must be the same color, and so \(P(n+1)\) is true. Thus, \(P(n)\) implies \(P(n+1)\).

By the principle of induction, \(P(n)\) is true for all \(n \geq 1\). \(\quad \blacksquare\)

We’ve proved something false! Does this mean that math broken and we should all take up poetry instead? Of course not! It just means that this proof has a mistake.

The mistake in this argument is in the sentence that begins “So \(h_1\) is the same color as the remaining horses besides \(h_{n+1}\)—that is \(h_2, \ldots, h_n\, \ldots\).” The ellipis notation (“\(\ldots\)”) in the expression “\(h_1, h_2, \ldots, h_n, h_{n+1}\)” creates the impression that there are some remaining horses—namely \(h_2, \ldots, h_n\) —besides \(h_1\) and \(h_{n+1}\) However, this is not true when \(n = 1\). In that case, \(h_1, h_2, \ldots, h_n, h_{n+1}\) is just \(h_1, h_2\) and there are no “remaining” horses for \(h_1\) to share a color with. And of course, in this case \(h_1\) and \(h_2\) really don’t need to be the same color.

This mistake knocks a critical link out of our induction argument. We proved \(P(1)\) and we correctly proved \(P(2) \rightarrow P(3), P(3) \rightarrow P(4)\), etc. But we failed to prove \(P(1) \rightarrow P(2)\), and so everything falls apart: we cannot conclude that \(P(2)\), \(P(3)\), etc., are true. And naturally, these propositions are all false; there are sets of \(n\) horses of different colors for all \(n\geq 2\).

Students sometimes explain that the mistake in the proof is because \(P(n)\) is false for \(n \geq 2\), and the proof assumes something false, \(P(n)\), in order to prove \(P(n+1)\). You should think about how to help such a student understand why this explanation would get no credit on a Math for Computer Science exam.

 

¹But see Section 5.3.

²Methods for finding such formulas are covered in Part III of the text.

³In the special case \(n = 0\), the whole courtyard consists of a single central square; otherwise, there are four central squares.

⁴5-choosability is a slight generalization of 5-colorability. Although every planar graph is 4- colorable and therefore 5-colorable, not every planar graph is 4-choosable. If this all sounds like nonsense, don’t panic. We’ll discuss graphs, planarity, and coloring in Part II of the text.