5.2: Strong Induction
- Page ID
- 48317
A useful variant of induction is called strong induction. Strong induction and ordinary induction are used for exactly the same thing: proving that a predicate is true for all nonnegative integers. Strong induction is useful when a simple proof that the predicate holds for \(n + 1\) does not follow just from the fact that it holds at \(n\), but from the fact that it holds for other values \(\leq n\).
A Rule for Strong Induction
Principle of Strong Induction.
Let \(P\) be a predicate on nonnegative integers. If
- \(P(0)\) is true, and
- for all \(n \in \mathbb{N}\), \(P(0)\), \(P(1)\), ..., \(P(n)\) together imply \(P(n+1)\),
then \(P(m)\) is true for all \(m \in \mathbb{N}\).
The only change from the ordinary induction principle is that strong induction allows you make more assumptions in the inductive step of your proof! In an ordinary induction argument, you assume that \(P(n)\) is true and try to prove that \(P(n+1)\) is also true. In a strong induction argument, you may assume that \(P(0)\), \(P(1)\), ..., and \(P(n)\) are all true when you go to prove \(P(n+1)\). So you can assume a stronger set of hypotheses which can make your job easier.
Formulated as a proof rule, strong induction is
Rule. Strong Induction Rule
\[\nonumber \frac{P(0), \quad \forall n \in \mathbb{N} .(P(0) \text { AND } P(1) \text { AND } \ldots \text { AND } P(n)) \text { IMPLIES } P(n+1)}{\forall m \in \mathbb{N} . P(m)}\]
Stated more succintly, the rule is
Rule.
\[\nonumber \frac{P(0), \quad[\forall k \leq n \in \mathbb{N} . P(k)] \text { IMPLIES } P(n+1)}{\forall m \in \mathbb{N} . P(m)}\]
The template for strong induction proofs is identical to the template given in Section 5.1.3 for ordinary induction except for two things:
- you should state that your proof is by strong induction, and
- you can assume that \(P(0), P(1), \ldots,\) and \(P(n)\) are all true instead of only \(P(n)\) during the inductive step.
Products of Primes
As a first example, we’ll use strong induction to re-prove Theorem 2.3.1 which we previously proved using Well Ordering.
Theorem
Every integer greater than 1 is a product of primes.
- Proof
-
We will prove the Theorem by strong induction, letting the induction hypothesis, \(P(n)\), be
\(n\) is a product of primes.
So the Theorem will follow if we prove that \(P(n)\) holds for all \(n \geq 2\).
Base Case: (n = 2): \(P(2)\) is true because 2 is prime, so it is a length one product of primes by convention.
Inductive step: Suppose that \(n \geq 2\) and that every number from 2 to \(n\) is a product of primes. We must show that \(P(n + 1)\) holds, namely, that \(n + 1\) is also a product of primes. We argue by cases:
If \(n + 1\) is itself prime, then it is a length one product of primes by convention, and so \(P(n+1)\) holds in this case.
Otherwise, \(n+1\) is not prime, which by definition means \(n+1 = k \cdot m\) for some integers \(k, m\) between 2 and \(n\). Now by the strong induction hypothesis, we know that both \(k\) and \(m\) are products of primes. By multiplying these products, it follows immediately that \(k \cdot m = n + 1\) is also a product of primes. Therefore, \(P(n + 1)\) holds in this case as well.
So \(P(n + 1)\) holds in any case, which completes the proof by strong induction that \(P(n)\) holds for all \(n \geq 2\). \(\quad \blacksquare\)
Making Change
The country Inductia, whose unit of currency is the Strong, has coins worth 3Sg (3 Strongs) and 5Sg. Although the Inductians have some trouble making small change like 4Sg or 7Sg, it turns out that they can collect coins to make change for any number that is at least 8 Strongs.
Strong induction makes this easy to prove for \(n + 1 \geq 11\), because then \((n + 1) - 3 \geq 8\), so by strong induction the Inductians can make change for exactly \((n + 1) - 3\) Strongs, and then they can add a 3Sg coin to get \((n+1)\) Sg. So the only thing to do is check that they can make change for all the amounts from 8 to 10Sg, which is not too hard to do.
Here’s a detailed writeup using the official format:
Proof. We prove by strong induction that the Inductians can make change for any amount of at least 8Sg. The induction hypothesis, \(P(n)\) will be:
There is a collection of coins whose value is \(n + 8\) Strongs.

We now proceed with the induction proof:
Base case: \(P(0)\) is true because a 3Sg coin together with a 5Sg coin makes 8Sg.
Inductive step: We assume \(P(k)\) holds for all \(k \leq n\), and prove that \(P(n + 1)\) holds. We argue by cases:
Case (\(n + 1 = 1\)): We have to make \(n + 1) + 8 =\) 9Sg. We can do this using three 3Sg coins.
Case (\(n + 1 = 2\)): We have to make \(n + 1) + 8 =\) 10Sg. Use two 5Sg coins.
Case (\(n + 1 \geq 3\)): Then \(0 \leq n - 2 \leq n\), so by the strong induction hypothesis, the Inductians can make change for \((n - 2) + 8\)Sg. Now by adding a 3Sg coin, they can make change for \((n + 1) + 8\)Sg, so \(P(n+1)\) holds in this case.
Since \(n \geq 0\), we know that \(n + 1 \geq 1\) and thus that the three cases cover every possibility. Since \(P(n + 1)\) is true in every case, we can conclude by strong induction that for all \(n \geq 0\), the Inductians can make change for \(n + 8\) Strong. That is, they can make change for any number of eight or more Strong. \(\quad \blacksquare\)
The Stacking Game
Here is another exciting game that’s surely about to sweep the nation! You begin with a stack of \(n\) boxes. Then you make a sequence of moves. In each move, you divide one stack of boxes into two nonempty stacks. The game ends when you have \(n\) stacks, each containing a single box. You earn points for each move; in particular, if you divide one stack of height \(a + b\) into two stacks with heights \(a\) and \(b\), then you score \(ab\) points for that move. Your overall score is the sum of the points that you earn for each move. What strategy should you use to maximize your total score?
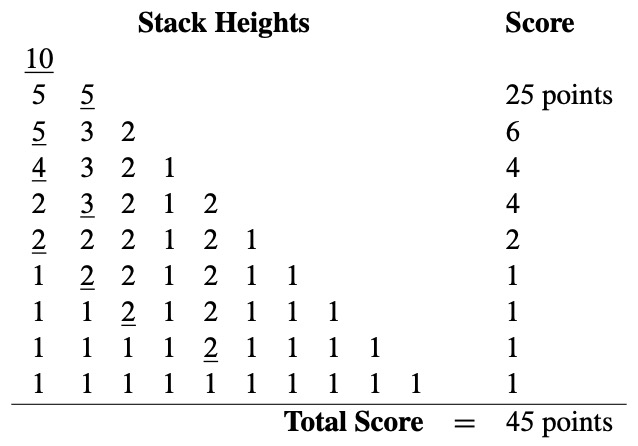
As an example, suppose that we begin with a stack of \(n = 10\) boxes. Then the game might proceed as shown in Figure 5.6. Can you find a better strategy?
Analyzing the Game
Let’s use strong induction to analyze the unstacking game. We’ll prove that your score is determined entirely by the number of boxes—your strategy is irrelevant!
Theorem \(\PageIndex{1}\)
Every way of unstacking \(n\) blocks gives a score of \(n(n - 1)/2\) points.
There are a couple technical points to notice in the proof:
- The template for a strong induction proof mirrors the one for ordinary induction.
- As with ordinary induction, we have some freedom to adjust indices. In this case, we prove \(P(1)\) in the base case and prove that \(P(1), \ldots , P(n)\) imply \(P(n + 1)\) for all \(n \geq 1\) in the inductive step.
- Proof
-
The proof is by strong induction. Let \(P(n)\) be the proposition that every way of unstacking \(n\) blocks gives a score of \(n(n - 1)/2\).
Base case: If \(n = 1\), then there is only one block. No moves are possible, and so the total score for the game is \(1(1 - 1)/2 = 0\). Therefore, \(P(1)\) is true.
Inductive step: Now we must show that \(P(1), \ldots, P(n)\) imply \(P(n+1)\) for all \(n \geq 1\). So assume that \(P(1), \ldots, P(n)\) are all true and that we have a stack of \(n+1\) blocks. The first move must split this stack into substacks with positive sizes \(a\) and \(b\) where \(a+b=n+1\) and \(0<a, b \leq n\). Now the total score for the game is the sum of points for this first move plus points obtained by unstacking the two resulting substacks:
\[\begin{aligned}
\text { total score }=&(\text { score for } 1 \text { st move }) \\
&+(\text { score for unstacking } a \text { blocks }) \\
&+(\text { score for unstacking } b \text { blocks }) \\
=& a b+\frac{a(a-1)}{2}+\frac{b(b-1)}{2} \quad \text { by } P(a) \text { and } P(b) \\
=& \frac{(a+b)^{2}-(a+b)}{2}=\frac{(a+b)((a+b)-1)}{2} \\
=& \frac{(n+1) n}{2}
\end{aligned}\]This shows that \(P(1), \ldots , P(n)\) imply \(P(n+1)\).
Therefore, the claim is true by strong induction. \(\quad \blacksquare\)


