11.4: Isomorphism

Last updated
Save as PDF

Page ID: 48369

Eric Lehman, F. Thomson Leighton, & Alberty R. Meyer
Google and Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Two graphs that look different might actually be the same in a formal sense. For example, the two graphs in Figure 11.7 are both 4-vertex, 5-edge graphs and you get graph (b) by a o 90 clockwise rotation of graph (a).

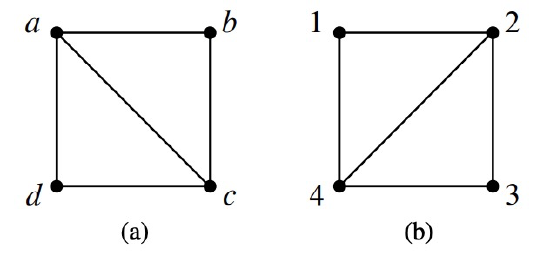
Strictly speaking, these graphs are different mathematical objects, but this difference doesn’t reflect the fact that the two graphs can be described by the same picture—except for the labels on the vertices. This idea of having the same picture “up to relabeling” can be captured neatly by adapting Definition 9.7.1 of isomorphism of digraphs to handle simple graphs. An isomorphism between two graphs is an edge-preserving bijection between their sets of vertices:

Definition \(\PageIndex{1}\)

An isomorphism between graphs \(G\) and \(H\) is a bijection \(f : V(G) \rightarrow V(H)\) such that

\[\nonumber \langle u - v\rangle \in E(G) \text{ iff } \langle f(u) - f(v)\rangle \in E(H)\]

for all \(u, v \in V(G)\). Two graphs are isomorphic when there is an isomorphism between them.

Here is an isomorphism, f , between the two graphs in Figure 11.7:

\[\begin{aligned} f(a) &::= 2 \qquad f(b) &::= 3 \\ f(c) &::= 4 \qquad f(d) &::= 1. \end{aligned}\]

You can check that there is an edge between two vertices in the graph on the left if and only if there is an edge between the two corresponding vertices in the graph on the right.

Two isomorphic graphs may be drawn very differently. For example, Figure 11.8 shows two different ways of drawing \(C_5\).

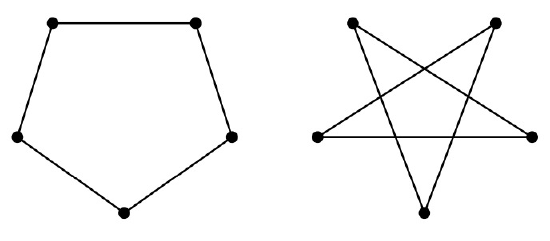
Notice that if \(f\) is an isomorphism between \(G\) and \(H\), then \(f^{-1}\) is an isomorphism between \(H\) and \(G\). Isomorphism is also transitive because the composition of isomorphisms is an isomorphism. In fact, isomorphism is an equivalence relation.

Isomorphism preserves the connection properties of a graph, abstracting out what the vertices are called, what they are made out of, or where they appear in a drawing of the graph. More precisely, a property of a graph is said to be preserved under isomorphism if whenever \(G\) has that property, every graph isomorphic to \(G\) also has that property. For example, since an isomorphism is a bijection between sets of vertices, isomorphic graphs must have the same number of vertices. What’s more, if \(f\) is a graph isomorphism that maps a vertex, \(v\), of one graph to the vertex, \(f(v)\), of an isomorphic graph, then by definition of isomorphism, every vertex adjacent to \(v\) in the first graph will be mapped by \(f\) to a vertex adjacent to \(f(v)\) in the isomorphic graph. Thus, \(v\) and \(f(v)\) will have the same degree. If one graph has a vertex of degree 4 and another does not, then they can’t be isomorphic. In fact, they can’t be isomorphic if the number of degree 4 vertices in each of the graphs is not the same.

Looking for preserved properties can make it easy to determine that two graphs are not isomorphic, or to guide the search for an isomorphism when there is one. It’s generally easy in practice to decide whether two graphs are isomorphic. However, no one has yet found a procedure for determining whether two graphs are isomorphic that is guaranteed to run in polynomial time on all pairs of graphs.³

Having such a procedure would be useful. For example, it would make it easy to search for a particular molecule in a database given the molecular bonds. On the other hand, knowing there is no such efficient procedure would also be valuable: secure protocols for encryption and remote authentication can be built on the hypothesis that graph isomorphism is computationally exhausting.

The definitions of bijection and isomorphism apply to infinite graphs as well as finite graphs, as do most of the results in the rest of this chapter. But graph theory focuses mostly on finite graphs, and we will too. In the rest of this chapter we’ll assume graphs are finite.

We’ve actually been taking isomorphism for granted ever since we wrote “\(K_n\) has \(n\) vertices. . . ” at the beginning of Section 11.3.

Graph theory is all about properties preserved by isomorphism.

³A procedure runs in polynomial time when it needs an amount of time of at most \(p(n)\), where \(n\) is the total number of vertices and \(p()\) is a fixed polynomial.