11.6: The Stable Marriage Problem

Let’s look at another man/woman matching problem with an equal number of men and women. The set up is that each person has preferences about who they would like to marry: each man has preference list of all the women, and each woman has a preference list of all of the men.

The preferences don’t have to be symmetric. That is, Jennifer might like Brad best, but Brad doesn’t necessarily like Jennifer best. The goal is to marry everyone: every man must marry exactly one woman and vice-versa—no polygamy. Moreover, we would like to find a matching between men and women that is stable in the sense that there is no pair of people who prefer one another to their spouses.

For example, suppose Brad likes Angelina best, and Angelina likes Brad best, but Brad and Angelina are married to other people, say Jennifer and Billy Bob. Now Brad and Angelina prefer each other to their spouses, which puts their marriages at risk. Pretty soon, they’re likely to start spending late nights together working on problem sets!

This unfortunate situation is illustrated in Figure 11.11, where the digits “1” and “2” near a man shows which of the two women he ranks first and second, respectively, and similarly for the women.

Figure 11.11 Preferences for four people. Both men like Angelina best and both women like Brad best.

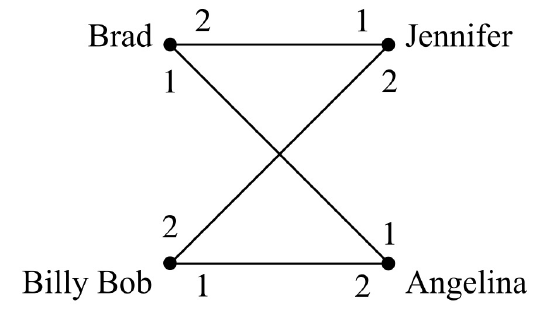
More generally, in any matching, a man and woman who are not married to each other and who like each other better than their spouses is called a rogue couple. In the situation shown in Figure 11.11, Brad and Angelina would be a rogue couple.

Having a rogue couple is not a good thing, since it threatens the stability of the marriages. On the other hand, if there are no rogue couples, then for any man and woman who are not married to each other, at least one likes their spouse better than the other, and so there won’t be any mutual temptation to start an affair.

Definition \(\PageIndex{1}\)

A stable matching is a matching with no rogue couples.

The question is, given everybody’s preferences, can you find a stable set of marriages? In the example consisting solely of the four people in Figure 11.11, we could let Brad and Angelina both have their first choices by marrying each other. Now neither Brad nor Angelina prefers anybody else to their spouse, so neither will be in a rogue couple. This leaves Jen not-so-happily married to Billy Bob, but neither Jen nor Billy Bob can entice somebody else to marry them, and so this is a stable matching.

It turns out there always is a stable matching among a group of men and women. We don’t know of any immediate way to recognize this, and it seems surprising. In fact, in the apparently similar “buddy” matching problem where people are supposed to be paired off as buddies, regardless of gender, a stable matching may not be possible. An example of preferences among four people where there is no stable buddy match is given in Problem 11.22. But when men are only allowed to marry women, and vice-versa, then we will be able to describe a simple procedure to produce a stable matching.⁶

The Mating Ritual

The procedure for finding a stable matching can be described in a memorable way as a Mating Ritual that takes place over several days. The following events happen each day:

Morning: Each man stands under the balcony of top choice among the women on his list, and he serenades her. He is said to be her suitor. If a man has no women left on his list, he stays home and does his math homework.

Afternoon: Each woman who has one or more suitors says to her favorite among them, “We might get engaged. Please stay around.” To the other suitors, she says, “No. I will never marry you! Take a hike!”

Evening: Any man who is told by a woman to take a hike crosses that woman off his preference list.

Termination condition: When a day arrives in which every woman has at most one suitor, the ritual ends with each woman marrying her suitor, if she has one.

There are a number of facts about this Mating Ritual that we would like to prove:

• The Ritual eventually reaches the termination condition.
• Everybody ends up married.
• The resulting marriages are stable

Mating Ritual at Akamai

The Internet infrastructure company Akamai, cofounded by Tom Leighton, also uses a variation of the Mating Ritual to assign web traffic to its servers.

In the early days, Akamai used other combinatorial optimization algorithms that got to be too slow as the number of servers (over 65,000 in 2010) and requests (over 800 billion per day) increased. Akamai switched to a Ritual-like approach, since a Ritual is fast and can be run in a distributed manner. In this case, web requests correspond to women and web servers correspond to men. The web requests have preferences based on latency and packet loss, and the web servers have preferences based on cost of bandwidth and co-location.

There is a Marriage Day

It’s easy to see why the Mating Ritual has a terminal day when people finally get married. Every day on which the ritual hasn’t terminated, at least one man crosses a woman off his list. (If the ritual hasn’t terminated, there must be some woman serenaded by at least two men, and at least one of them will have to cross her off his list). If we start with \(n\) men and \(n\) women, then each of the \(n\) men’s lists initially has \(n\) women on it, for a total of \(n^2\) list entries. Since no women ever gets added to a list, the total number of entries on the lists decreases every day that the Ritual continues, and so the Ritual can continue for at most \(n^2\) days.

They All Live Happily Ever After. . .

We will prove that the Mating Ritual leaves everyone in a stable marriage. To do this, we note one very useful fact about the Ritual: if on some morning a woman has any suitor, then her favorite suitor will still be serenading her the next morning—his list won’t have changed. So she is sure to have today’s favorite suitor among her suitors tomorrow. That means she will be able to choose a favorite suitor tomorrow who is at least as desirable to her as today’s favorite. So day by day, her favorite suitor can stay the same or get better, never worse. This sounds like an invariant, and it is.

Definition \(\PageIndex{2}\)

Let \(P\) be the predicate: for every woman, \(w\), and man, \(m\), if w is crossed off \(m\)’s list, then \(w\) has a suitor whom she prefers over \(m\).

Lemma 11.6.3. \(P\) is a preserved invariant for The Mating Ritual.

Proof. Woman \(w\) gets crossed off \(m\)’s list only when \(w\) has a suitor she prefers to \(m\). Thereafter, her favorite suitor doesn’t change until one she likes better comes along. So if her favorite suitor was preferable to \(m\), then any new favorite suitor will be as well.

Notice that the invariant \(P\) holds vacuously at the beginning since no women are crossed off to start. So by the Invariant Principle, \(P\) holds throughout the Ritual. Now we can prove:

Theorem \(\PageIndex{4}\)

Everyone is married at the end of the Mating Ritual.

Proof

Assume to the contrary that on the last day of the Mating Ritual, some man—call him Bob—is not married. This means Bob can’t be serenading anybody, that is, his list must be empty. So every woman must have been crossed off his list and, since \(P\) is true, every woman has a suitor whom she prefers to Bob. In particular, every woman has some suitor, and since it is the last day, they have only one suitor, and this is who they marry. But there are an equal number of men and women, so if all women are married, so are all men, contradicting the assumption that Bob is not married. \(\quad \blacksquare\)

Theorem \(\PageIndex{5}\)

The Mating Ritual produces a stable matching.

Proof

Let Brad and Jen be any man and woman, respectively, that are not married to each other on the last day of the Mating Ritual. We will prove that Brad and Jen are not a rogue couple, and thus that all marriages on the last day are stable. There are two cases to consider.

Case 1: Jen is not on Brad’s list by the end. Then by invariant \(P\), we know that Jen has a suitor (and hence a husband) whom she prefers to Brad. So she’s not going to run off with Brad—Brad and Jen cannot be a rogue couple.

Case 2: Jen is on Brad’s list. Since Brad picks women to serenade by working down his list, his wife must be higher on his preference list than Jen. So he’s not going to run off with Jen—once again, Brad and Jen are not a rogue couple. \(\quad \blacksquare\)

. . Especially the Men

Who is favored by the Mating Ritual, the men or the women? The women seem to have all the power: each day they choose their favorite suitor and reject the rest. What’s more, we know their suitors can only change for the better as the Ritual progresses. Similarly, a man keeps serenading the woman he most prefers among those on his list until he must cross her off, at which point he serenades the next most preferred woman on his list. So from the man’s perspective, the woman he is serenading can only change for the worse. Sounds like a good deal for the women.

But it’s not! We will show that the men are by far the favored gender under the Mating Ritual.

While the Mating Ritual produces one stable matching, stable matchings need not be unique. For example, reversing the roles of men and women will often yield a different stable matching among them. So a man may have different wives in different sets of stable marriages. In some cases, a man can stably marry every one of the woman, but in most cases, there are some woman who cannot be a man’s wife in any stable matching. For example, given the preferences shown in Figure 11.11, Jennifer cannot be Brad’s wife in any stable matching because if he was married to her, then he and Angelina would be a rogue couple. It is not feasible for Jennifer to be stably married to Brad.

Definition \(\PageIndex{6}\)

Given a set of preferences for the men and women, one person is a feasible spouse for another person when there is a stable matching in which these two people are married.

Definition \(\PageIndex{7}\)

Let \(Q\) be the predicate: for every woman, \(w\), and man, \(m\), if \(w\) is crossed off \(m\)’s list, then \(w\) is not a feasible spouse for \(m\).

Lemma 11.6.8. \(Q\) is a preserved invariant for The Mating Ritual.

Proof. Suppose \(Q\) holds at some point in the Ritual and some woman, Alice, is about to be crossed off some man’s, Bob’s, list. We claim that Alice must not be feasible for Bob. Therefore \(Q\) will still hold after Alice is crossed off, proving that \(Q\) is invariant

To verify the claim, notice that when Alice gets crossed of Bob’s list, it’s because Alice has a suitor, Ted, she prefers to Bob. What’s more since \(Q\) holds, all Ted’s feasible wives are still on his list, and Alice is at the top. So Ted likes Alice better than all his other feasible spouses. Now if Alice could be married to Bob in some set of stable marriages, then Ted must be married to a wife he likes less than Alice, making Alice and Ted a rogue couple and contradicting stability. So Alice can’t be married to Bob, that is, Alice is not a feasible wife for Bob, as claimed. \(\quad \blacksquare\)

Definition \(\PageIndex{9}\)

A person’s optimal spouse is their most preferred feasible spouse. A person’s pessimal spouse is their least preferred feasible spouse.

Everybody has an optimal and a pessimal spouse, since we know there is at least one stable matching, namely, the one produced by the Mating Ritual. Lemma 11.6.8 implies a key property the Mating Ritual:

Theorem \(\PageIndex{10}\)

The Mating Ritual marries every man to his optimal spouse and every woman to her pessimal spouse.

Proof

If Bob is married to Alice on the final day of the Ritual, then everyone above Alice on Bob’s preference list was crossed off, and by property \(Q\), all these crossed off women were infeasible for Bob. So Alice is Bob’s highest ranked feasible spouse, that is, his optimal spouse.

Further, since Bob likes Alice better than any other feasible wife, Alice and Bob would be a rogue couple if Alice was married to a husband she liked less than Bob. So Bob must be Alice’s least preferred feasible husband. \(\quad \blacksquare\)

Applications

The Mating Ritual was first announced in a paper by D. Gale and L.S. Shapley in 1962, but ten years before the Gale-Shapley paper was published, and unknown to them, a similar algorithm was being used to assign residents to hospitals by the National Resident Matching Program (NRMP). The NRMP has, since the turn of the twentieth century, assigned each year’s pool of medical school graduates to hospital residencies (formerly called “internships”), with hospitals and graduates playing the roles of men and women.⁷ Before the Ritual-like algorithm was adopted, there were chronic disruptions and awkward countermeasures taken to preserve unstable assignments of graduates to residencies. The Ritual resolved these problems so successfully, that it was used essentially without change at least through 1989.⁸ For this and related work, Shapley was awarded the 2012 Nobel prize in Economics.

Not surprisingly, the Mating Ritual is also used by at least one large online dating agency. Of course there is no serenading going on—everything is handled by computer.

⁶Once again, we disclaim any political statement here—it’s just the way that the math works out.

⁷In this case there may be multiple women married to one man, but this is a minor complication, see Problem 11.23.

⁸Much more about the Stable Marriage Problem can be found in the very readable mathematical monograph by Dan Gusfield and Robert W. Irving, [24].