11.8: Simple Walks

Walks, Paths, Cycles in Simple Graphs

Walks and paths in simple graphs are esentially the same as in digraphs. We just modify the digraph definitions using undirected edges instead of directed ones. For example, the formal definition of a walk in a simple graph is a virtually the same as the Definition 9.2.1 of a walk in a digraph:

Definition \(\PageIndex{1}\)

A walk in a simple graph, \(G\), is an alternating sequence of vertices and edges that begins with a vertex, ends with a vertex, and such that for every edge \(\langle u - v \rangle\) in the walk, one of the endpoints \(u, v\) is the element just before the edge, and the other endpoint is the next element after the edge. The length of a walk is the total number of occurrences of edges in it.

So a walk, \(\textbf{v}\), is a sequence of the form

where \(\langle v_i - v_{i+1} \rangle \in E(G)\) for \(i \in [0..k)\). The walk is said to start at \(v_0\), to end at \(v_k\), and the length, \(|\textbf{v}|\), of the walk is \(k\). The walk is a path iff all the \(v_i\)'s are different, that is, if \(i \neq j\), then \(v_i \neq v_j\).

A closed walk is a walk that begins and ends at the same vertex. A single vertex counts as a length zero closed walk as well as a length zero path.

A cycle is a closed walk of length three or more whose vertices are distinct except for the beginning and end vertices

Note that in contrast to digraphs, we don’t count length two closed walks as cycles in simple graphs. That’s because a walk going back and forth on the same edge is always possible in a simple graph, and it has no importance. Also, there are no closed walks of length one, since simple graphs don’t have self loops.

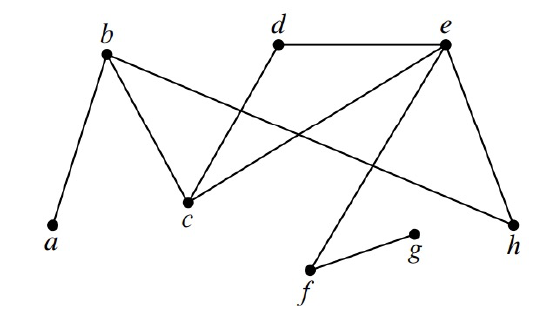
As in digraphs, the length of a walk is one less than the number of occurrences of vertices in it. For example, the graph in Figure 11.15 has a length 6 path through the seven successive vertices \(abcdefg\). This is the longest path in the graph. The graph in Figure 11.15 also has three cycles through successive vertices \(bhecb\), \(cdec\), and \(bcdehb\).

Figure 11.15 A graph with 3 cycles: \(bhecb, cdec, bcdehb\).

Cycles as Subgraphs

A cycle does not really have a beginning or an end, so it can be described by any of the paths that go around it. For example, in the graph in Figure 11.15, the cycle starting at \(b\) and going through vertices \(bcdehb\) can also be described as starting at \(d\) and going through \(dehbcd\). Furthermore, cycles in simple graphs don’t have a direction: \(dcbhed\) describes the same cycle as though it started and ended at \(d\) but went in the opposite direction.

A precise way to explain which closed walks describe the same cycle is to define cycle as a subgraph instead of as a closed walk. Specifically, we could define a cycle in \(G\) to be a subgraph of \(G\) that looks like a length-\(n\) cycle for \(n \geq 3\).

Definition \(\PageIndex{2}\)

A graph \(G\) is said to be a subgraph of a graph \(H\) if \(V(G) \subseteq V(H)\) and \(E(G) \subseteq E(H).\)

For example, the one-edge graph \(G\) where

\[\nonumber V(G) = \{g, h, i\} \text{ and } E(G) = \{ \langle h - i \rangle\}\]

is a subgraph of the graph \(H\) in Figure 11.1. On the other hand, any graph containing an edge \(\langle g-h \rangle\) will not be a subgraph of \(H\) because this edge is not in \(E(H)\). Another example is an empty graph on \(n\) nodes, which will be a subgraph of an \(L_n\) with the same set of nodes; similarly, \(L_n\) is a subgraph of \(C_n\), and \(C_n\)is a subgraph of \(K_n\).

Definition \(\PageIndex{3}\)

For \(n \geq 3\), let \(C_n\) be the graph with vertices \(1, \ldots, n\) and edges

\[\nonumber \langle 1-2 \rangle, \langle 2-3 \rangle, \ldots, \langle (n-1)-n \rangle, \langle n-1 \rangle.\]

A cycle of a graph, \(G\), is a subgraph of \(G\) that is isomorphic to \(C_n\) for some \(n \geq 3\).

This definition formally captures the idea that cycles don’t have direction or beginnings or ends.