13.4: Hanging Out Over the Edge

Suppose you have a bunch of books and you want to stack them up, one on top of another in some off-center way, so the top book sticks out past books below it without falling over. If you moved the stack to the edge of a table, how far past the edge of the table do you think you could get the top book to go? Could the top book stick out completely beyond the edge of table? You’re not supposed to use glue or any other support to hold the stack in place.

Most people’s first response to the Book Stacking Problem—sometimes also their second and third responses—is “No, the top book will never get completely past the edge of the table.” But in fact, you can get the top book to stick out as far as you want: one booklength, two booklengths, any number of booklengths!

Formalizing the Problem

We’ll approach this problem recursively. How far past the end of the table can we get one book to stick out? It won’t tip as long as its center of mass is over the table, so we can get it to stick out half its length, as shown in Figure 13.4.

Figure 13.4 One book can overhang half a book length.

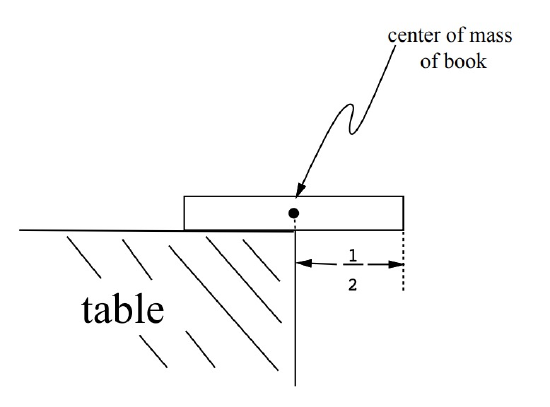
Now suppose we have a stack of books that will not tip over if the bottom book rests on the table—call that a stable stack. Let’s define the overhang of a stable stack to be the horizontal distance from the center of mass of the stack to the furthest edge of the top book. So the overhang is purely a property of the stack, regardless of its placement on the table. If we place the center of mass of the stable stack at the edge of the table as in Figure 13.5, the overhang is how far we can get the top book in the stack to stick out past the edge.

Figure 13.5 Overhanging the edge of the table.

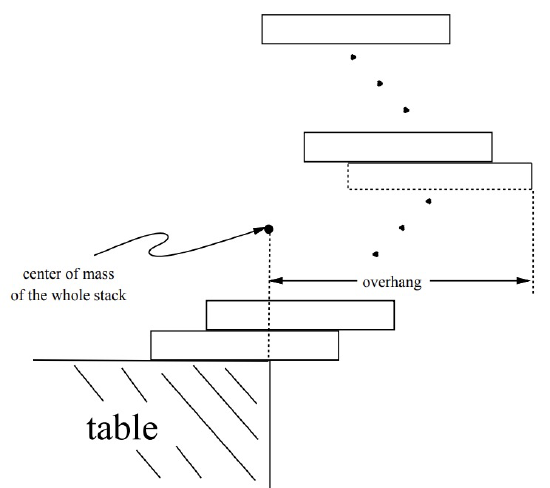
In general, a stack of n books will be stable if and only if the center of mass of the top \(i\) books sits over the \((i+1)\)st book for \(i = 1, 2, \ldots, n-1.\)

So we want a formula for the maximum possible overhang, \(B_n\), achievable with a stable stack of \(n\) books.

We’ve already observed that the overhang of one book is 1/2 a book length. That is,

\[\nonumber B_1 = \dfrac{1}{2}.\]

Now suppose we have a stable stack of \(n + 1\) books with maximum overhang. If the overhang of the \(n\) books on top of the bottom book was not maximum, we could get a book to stick out further by replacing the top stack with a stack of \(n\) books with larger overhang. So the maximum overhang, \(B_{n+1}\), of a stack of \(n + 1\) books is obtained by placing a maximum overhang stable stack of \(n\) books on top of the bottom book. And we get the biggest overhang for the stack of \(n + 1\) books by placing the center of mass of the \(n\) books right over the edge of the bottom book as in Figure 13.6.

Figure 13.6 Additional overhang with \(n + 1\) books.

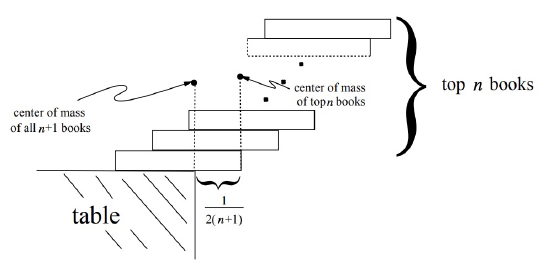
So we know where to place the \(n + 1\)st book to get maximum overhang. In fact, the reasoning above actually shows that this way of stacking \(n + 1\) books is the unique way to build a stable stack where the top book extends as far as possible. All we have to do is calculate what this extension is.

The simplest way to do that is to let the center of mass of the top \(n\) books be the origin. That way the horizontal coordinate of the center of mass of the whole stack of \(n + 1\) books will equal the increase in the overhang. But now the center of mass of the bottom book has horizontal coordinate \(1/2\), so the horizontal coordinate of center of mass of the whole stack of \(n + 1\) books is

\[\nonumber \dfrac{0 \cdot n + (1/2) \cdot 1}{n + 1} = \dfrac{1}{2(n+1)}.\]

In other words,

\[\label{13.4.1} B_{n+1} = B_n + \dfrac{1}{2(n+1)},\]

as shown in Figure 13.6.

Expanding equation(\ref{13.4.1}), we have

\[\begin{align} \nonumber B_{n+1} &= B_{n-1} + \dfrac{1}{2n} + \dfrac{1}{2(n+1)} \\ \nonumber &= B_1 + \dfrac{1}{2 \cdot 2} + \cdots + \dfrac{1}{2n} + \dfrac{1}{2(n+1)} \\ \label{13.4.2} &= \dfrac{1}{2} \sum_{i=1}^{n+1}\dfrac{1}{i}. \end{align}\]

So our next task is to examine the behavior of \(B_n\) as \(n\) grows.

Harmonic Numbers

Definition \(\PageIndex{1}\)

The \(n\)th harmonic number, \(H_n\), is

\[\nonumber H_n ::= \sum_{i=1}{n} \dfrac{1}{i}.\]

So (\ref{13.4.2}) means that

\[\nonumber B_n = \dfrac{H_n}{2}.\]

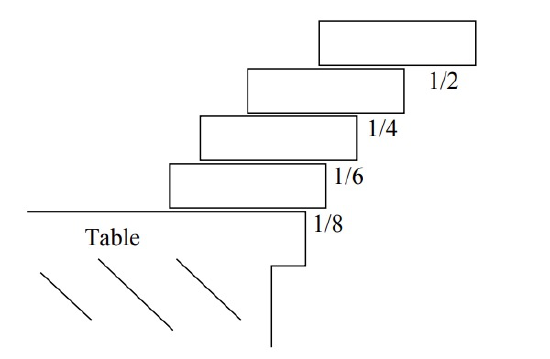
The first few harmonic numbers are easy to compute. For example, \(H_4 = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} = \frac{25}{12} > 2.\) The fact that \(H_4\) is greater than 2 has special significance: it implies that the total extension of a 4-book stack is greater than one full book! This is the situation shown in Figure 13.7.

Figure 13.7 Stack of four books with maximum overhang.

There is good news and bad news about harmonic numbers. The bad news is that there is no known closed-form expression for the harmonic numbers. The good news is that we can use Theorem 13.3.2 to get close upper and lower bounds on \(H_n\). In particular, since

\[\nonumber \int_{1}^{n} \dfrac{1}{x}dx = \ln (x) \bigg|_{1}^{n} = \ln (n),\]

Theorem 13.3.2 means that

\[\ln (n) + \dfrac{1}{n} \leq H_n \leq \ln (n) + 1.\]

In other words, the \(n\)th harmonic number is very close to \(\ln (n)\).

Because the harmonic numbers frequently arise in practice, mathematicians have worked hard to get even better approximations for them. In fact, it is now known that

\[\label{13.4.4} H_n = \ln (n) + \gamma + \dfrac{1}{2n} + \dfrac{1}{12n^2} + \dfrac{\epsilon (n)}{120n^4}\]

Here \(\gamma\) is a value 0.577215664... called Euler’s constant, and \(\epsilon(n)\) is between 0 and 1 for all \(n\). We will not prove this formula.

We are now finally done with our analysis of the book stacking problem. Plugging the value of \(H_n\) into (\ref{13.4.2}), we find that the maximum overhang for \(n\) books is very close to \(1/2 \ln(n)\). Since \(\ln(n)\) grows to infinity as \(n\) increases, this means that if we are given enough books we can get a book to hang out arbitrarily far over the edge of the table. Of course, the number of books we need will grow as an exponential function of the overhang; it will take 227 books just to achieve an overhang of 3, never mind an overhang of 100.

Extending Further Past the End of the Table

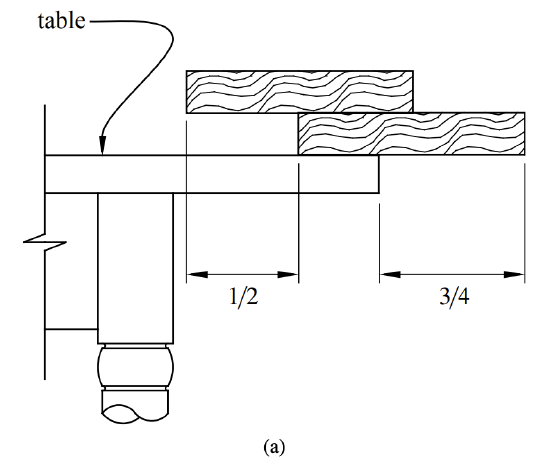
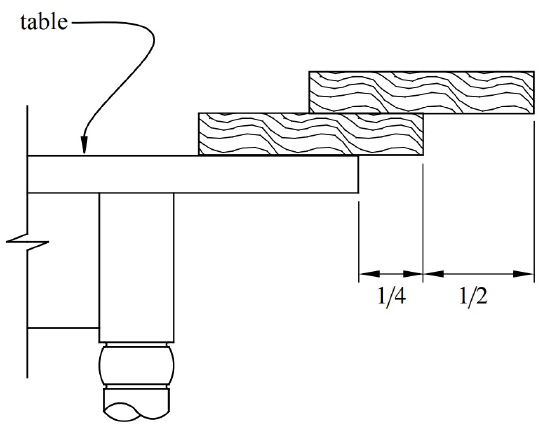
The overhang we analyzed above was the furthest out the top book could extend past the table. This leaves open the question of if there is some better way to build a stable stack where some book other than the top stuck out furthest. For example, Figure 13.8 shows a stable stack of two books where the bottom book extends further out than the top book. Moreover, the bottom book extends 3/4 of a book length past the end of the table, which is the same as the maximum overhang for the top book in a two book stack.

Since the two book arrangement in Figure 13.8(a) ties the maximum overhang stack in Figure 13.8(b), we could take the unique stable stack of \(n\) books where the top book extends furthest, and switch the top two books to look like Figure 13.8(a). This would give a stable stack of \(n\) books where the second from the top book extends the same maximum overhang distance. So for \(n > 1\), there are at least two ways of building a stable stack of \(n\) books which both extend the maximum overhang distance—one way where the top book is furthest out, and another way where the second from the top book is furthest out.

Figure 13.8 Figure (a) shows a stable stack of two books where the bottom book extends the same amount past the end of the table as the maximum overhang twobook stack shown in Figure (b).

It turns out that there is no way to beat these two ways of making stable stacks. In fact, it’s not too hard to show that these are the only two ways to get a stable stack of books that achieves maximum overhang.

But there is more to the story. All our reasoning above was about stacks in which one book rests on another. It turns out that by building structures in which more than one book rests on top of another book—think of an inverted pyramid—it is possible to get a stack of \(n\) books to extend proportional to \(\sqrt[3]{n}\)—much more than \(\ln n\)—book lengths without falling over. See [13], Maximum Overhang.

Asymptotic Equality

For cases like Equation \ref{13.4.4} where we understand the growth of a function like \(H_n\) up to some (unimportant) error terms, we use a special notation, ~, to denote the leading term of the function. For example, we say that \(H_n ~ \ln (n)\) to indicate that the leading term of \(H_n\) is \(\ln (n)\). More precisely:

Definition \(\PageIndex{2}\)

For functions \(f, g : \mathbb{R} \rightarrow \mathbb{R}\), we say \(f\) is asymptotically equal to \(g\), in symbols,

\[\nonumber f(x) \sim g(x)\]

\iff

\[\nonumber \lim_{x \rightarrow \infty} f(x) / g(x) = 1.\]

Although it is tempting to write \(H_n \sim \ln (n) + \gamma\) to indicate the two leading terms, this is not really right. According to Definition 13.4.2, \(H_n \sim \ln (n) + c\) where \(c\) is any constant. The correct way to indicate that \(\gamma\) is the second-largest term is \(H_n - \ln(n) \sim \gamma\).

The reason that the ~ notation is useful is that often we do not care about lower order terms. For example, if \(n = 100\), then we can compute \(H(n)\) to great precision using only the two leading terms:

\[\nonumber |H_n - \ln(n) - \gamma| \leq |\dfrac{1}{200} - \dfrac{1}{120000} + \dfrac{1}{120 \cdot 100^4}| < \dfrac{1}{200}.\]

We will spend a lot more time talking about asymptotic notation at the end of the chapter. But for now, let’s get back to using sums.