13.5: Products
- Page ID
- 48390
We’ve covered several techniques for finding closed forms for sums but no methods for dealing with products. Fortunately, we do not need to develop an entirely new set of tools when we encounter a product such as
\[n! ::= \prod_{i = 1}^{n} i.\]
That’s because we can convert any product into a sum by taking a logarithm. For example, if
\[\nonumber P = \prod_{i = 1}^{n} f(i),\]
then
\[\nonumber \ln (P) = \sum_{i = 1}^{n} \ln (f(i)).\]
We can then apply our summing tools to find a closed form (or approximate closed form) for \(\ln(P)\) and then exponentiate at the end to undo the logarithm.
For example, let’s see how this works for the factorial function \(n!\). We start by taking the logarithm:
\[\begin{aligned} \ln (n!) &= \ln (1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n) \\ &= \ln(1) + \ln(2) + \ln(3) + \cdots + \ln(n - 1) + \ln(n) \\ &= \sum_{i = 1}^{n} \ln(i). \end{aligned}\]
Unfortunately, no closed form for this sum is known. However, we can apply Theorem 13.3.2 to find good closed-form bounds on the sum. To do this, we first compute
\[\begin{aligned} \int_{1}^{n} \ln(x) dx &= x \ln(x) - x \bigg|_{1}^{n} \\ &= n \ln(n) - n + 1. \end{aligned}\]
Plugging into Theorem 13.3.2, this means that
\[\nonumber n \ln(n) - n + 1 \leq \sum_{i=1}^{n} \ln(i) \leq n \ln(n) - n + 1 + \ln(n).\]
Exponentiating then gives
\[\dfrac{n^n}{e^{n-1}} \leq n! \leq \dfrac{n^{n+1}}{e^{n-1}}\]
This means that \(n!\) is within a factor of \(n\) of \(n^n / e^{n-1}\).
Stirling’s Formula
The most commonly used product in discrete mathematics is probably \(n!\), and mathematicians have workedto find tight closed-form bounds on its value. The most useful bounds are given in Theorem 13.5.1.
Theorem \(\PageIndex{1}\)
(Stirling’s Formula). For all \(n \geq 1\),
\[\nonumber n! = \sqrt{2\pi n} \left( \dfrac{n}{e} \right)^n e^{\epsilon(n)}\]
where
\[\nonumber \dfrac{1}{12n + 1} \leq \epsilon(n) \leq \dfrac{1}{12n}.\]
Theorem 13.5.1 can be proved by induction (with some pain), and there are lots of proofs using elementary calculus, but we won’t go into them.
There are several important things to notice about Stirling’s Formula. First, \(\epsilon(n)\) is always positive. This means that
\[n! > \sqrt{2\pi n} \left( \dfrac{n}{e} \right)^n\]
for all \(n \in \mathbb{N}^+\).
Second, \(\epsilon (n)\) tends to zero as \(n\) gets large. This means that
\[n! \sim \sqrt{2\pi n} \left( \dfrac{n}{e} \right)^n\]
which is impressive. After all, who would expect both \(\pi\) and \(e\) to show up in a closed-form expression that is asymptotically equal to \(n!\)?
Third, \(\epsilon(n)\)is small even for small values of \(n\). This means that Stirling’s Formula provides good approximations for \(n!\) for most all values of \(n\). For example, if we use
\[\nonumber \sqrt{2 \pi n} \left( \dfrac{n}{e} \right)^n\]
as the approximation for \(n!\), as many people do, we are guaranteed to be within a factor of
\[\nonumber e^{\epsilon(n)} \leq e^{\frac{1}{12n}}\]
of the correct value. For \(n \geq 10\), this means we will be within 1% of the correct value. For \(n \geq 100\), the error will be less than 0.1%.
If we need an even closer approximation for \(n!\), then we could use either
\[\nonumber \sqrt{2\pi n} \left( \dfrac{n}{e} \right)^n e^{1/12n}\]
or
\[\nonumber \sqrt{2\pi n} \left( \dfrac{n}{e} \right)^n e^{1/(12n+1)}\]
depending on whether we want an upper, or a lower, bound. By Theorem 13.5.1, we know that both bounds will be within a factor of
\[\nonumber e^{\frac{1}{12n} - \frac{1}{12n+1}} = e^{\frac{1}{144n^2 + 12n}}\]
of the correct value. For \(n \geq 10\), this means that either bound will be within 0.01% of the correct value. For \(n \geq 100\), the error will be less than 0.0001%.
For quick future reference, these facts are summarized in Corollary 13.5.2 and Table 13.1.
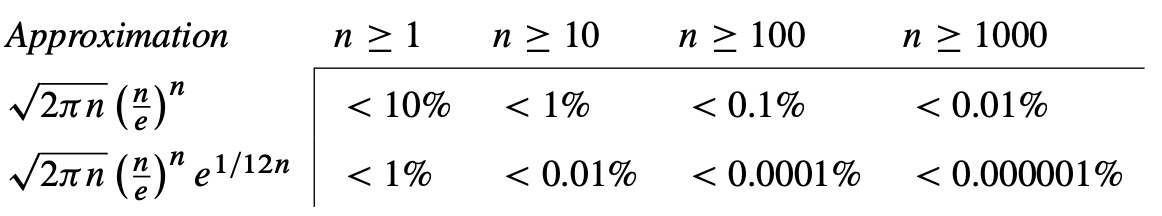
Corollary 13.5.2.
\(n! < \sqrt{2 \pi n} \dfrac{n}{e}^n \cdot \left\{\begin{array}{ll} 1.09 & \textit{for} n \geq 1, \\ 1.009 & \textit{for} n \geq 10, \\ 1.0009 & \textit{for} n \geq 100. \end{array}\right.\)


