20.2: Random Walks on Graphs

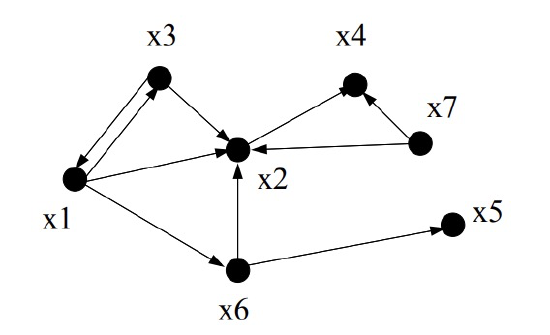
The hyperlink structure of the World Wide Web can be described as a digraph. The vertices are the web pages with a directed edge from vertex \(x\) to vertex \(y\) if \(x\) has a link to \(y\). For example, in the following graph the vertices \(x_1,\ldots,x_n\) correspond to web pages and \(\langle x_i \rightarrow x_j \rangle\) is a directed edge when page \(x_i\) contains a hyperlink to \(x_j\).

The web graph is an enormous graph with trillions of vertices. In 1995, two students at Stanford, Larry Page and Sergey Brin, realized that the structure of this graph could be very useful in building a search engine. Traditional document searching programs had been around for a long time and they worked in a fairly straightforward way. Basically, you would enter some search terms and the searching program would return all documents containing those terms. A relevance score might also be returned for each document based on the frequency or position that the search terms appeared in the document. For example, if the search term appeared in the title or appeared 100 times in a document, that document would get a higher score.

This approach works fine if you only have a few documents that match a search term. But on the web, there are many billions of documents and millions of matches to a typical search. For example, on May 2, 2012, a search on Google for “ ‘Mathematics for Computer Science’ text” gave 482,000 hits! Which ones should we look at first? Just because a page gets a high keyword score—say because it has “Mathematics Mathematics ... Mathematics” copied 200 times across the front of the document—does not make it a great candidate for attention. The web is filled with bogus websites that repeat certain words over and over in order to attract visitors.

Google’s enormous market capital in part derives from the revenue it receives from advertisers paying to appear at the top of search results. That top placement would not be worth much if Google’s results were as easy to manipulate as keyword frquencies. Advertisers pay because Google’s ranking method is consistently good at determining the most relevant web pages. For example, Google demonstrated its accuracy in our case by giving first rank² to our 6.042 text.

So how did Google know to pick our text to be first out of 482,000?—because back in 1995 Larry and Sergey got the idea to allow the digraph structure of the web to determine which pages are likely to be the most important.

First Crack at Page Rank

Looking at the web graph, do you have an idea which vertex/page might be the best to rank first? Assume that all the pages match the search terms for now. Well, intuitively, we should choose \(x_2\), since lots of other pages point to it. This leads us to their first idea: try defining the page rank of \(x\) to be \(\text{indegree}(x)\), the number of links pointing to \(x\). The idea is to think of web pages as voting for the most important page—the more votes, the better the rank.

Unfortunately, there are some problems with this idea. Suppose you wanted to have your page get a high ranking. One thing you could do is to create lots of dummy pages with links to your page.

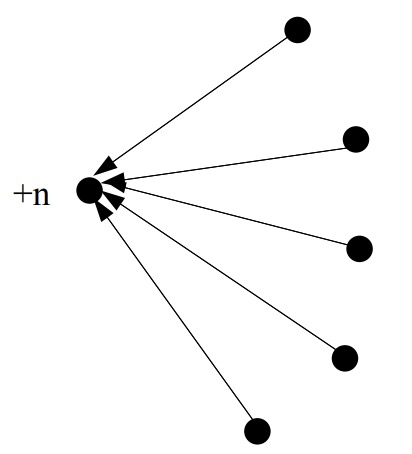
There is another problem—a page could become unfairly influential by having lots of links to other pages it wanted to hype

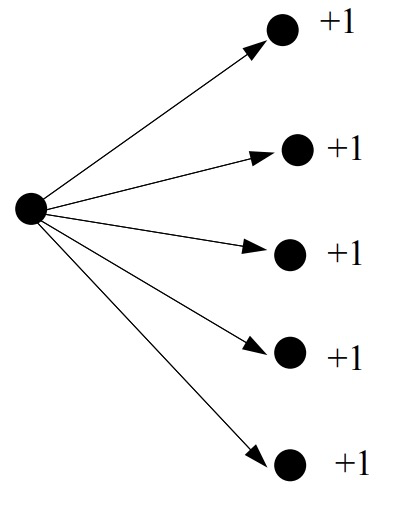
So this strategy for high ranking would amount to, “vote early, vote often,” which is no good if you want to build a search engine that’s worth paying fees for. So, admittedly, their original idea was not so great. It was better than nothing, but certainly not worth billions of dollars.

Random Walk on the Web Graph

But then Sergey and Larry thought some more and came up with a couple of improvements. Instead of just counting the indegree of a vertex, they considered the probability of being at each page after a long random walk on the web graph. In particular, they decided to model a user’s web experience as following each link on a page with uniform probability. For example, if the user is at page \(x\), and there are three links from page \(x\), then each link is followed with probability \(1/3\). More generally, they assigned each edge \(x \rightarrow y\) of the web graph with a probability conditioned on being on page \(x\):

\[\nonumber \text{Pr}[\text{follow link } \langle x \rightarrow y \rangle \mid \text{ at page } x] ::= \frac{1}{\text{outdeg}(x)}.\]

The simulated user experience is then just a random walk on the web graph.

We can also compute the probability of arriving at a particular page, \(y\), by summing over all edges pointing to \(y\). We thus have

\[\begin{align} \nonumber \text{Pr}[\text{go to }y] &= \sum_{\text{edges } \langle x \rightarrow y \rangle} \text{Pr}[\text{follow link } \langle x \rightarrow y \rangle \mid \text{ at page } x] \cdot \text{Pr}[\text{at page } x] \\ \label{20.2.1} &= \sum_{\text{edges } \langle x \rightarrow y \rangle} \frac{\text{Pr}[\text{at } x]}{\text{outdeg}(x)} \end{align}\]

For example, in our web graph, we have

\[\nonumber \text{Pr}[\text{go to } x_4] = \frac{\text{Pr}[\text{at } x_7]}{2} + \frac{\text{Pr}[\text{at } x_2]}{1}.\]

One can think of this equation as \(x_7\) sending half its probability to \(x_2\) and the other half to \(x_4\). The page \(x_2\) sends all of its probability to \(x_4\).

There’s one aspect of the web graph described thus far that doesn’t mesh with the user experience—some pages have no hyperlinks out. Under the current model, the user cannot escape these pages. In reality, however, the user doesn’t fall off the end of the web into a void of nothingness. Instead, he restarts his web journey. Moreover, even if a user does not get stuck at a dead end, they will commonly get discouraged after following some unproductive path for a while and will decide to restart.

To model this aspect of the web, Sergey and Larry added a supervertex to the web graph and added an edge from every page to the supervertex. Moreover, the supervertex points to every other vertex in the graph with equal probability, allowing the walk to restart from a random place. This ensures that the graph is strongly connected.

If a page had no hyperlinks, then its edge to the supervertex has to be assigned probability one. For pages that had some hyperlinks, the additional edge pointing to the supervertex was assigned some specially given probability. In the original versions of Page Rank, this probability was arbitrarily set to 0.15. That is, each vertex with outdegree \(n \geq 1\) got an additional edge pointing to the supervertex with assigned probability 0.15; its other \(n\) outgoing edges were still kept equally likely, that is, each of the \(n\) edges was assigned probability \(0.85/n\).

Stationary Distribution & Page Rank

The basic idea behind page rank is finding a stationary distribution over the web graph, so let’s define a stationary distribution.

Suppose each vertex is assigned a probability that corresponds, intuitively, to the likelihood that a random walker is at that vertex at a randomly chosen time. We assume that the walk never leaves the vertices in the graph, so we require that

\[\label{20.2.2} \sum_{\text{vertices }x} \text{Pr}[\text{at } x] = 1.\]

Definition \(\PageIndex{1}\)

An assignment of probabilities to vertices in a digraph is a stationary distribution if for all vertices \(x\)

\[\nonumber \text{Pr}[\text{at } x] = \text{Pr}[\text{go to } x \text{ at next step}]\]

Sergey and Larry defined their page ranks to be a stationary distribution. They did this by solving the following system of linear equations: find a nonnegative number, \(\text{Rank}(x)\), for each vertex, \(x\), such that

\[\label{20.2.3} \text{Rank}(x) = \sum_{\text{edges } \langle y \rightarrow x \rangle} \frac{\text{Rank}(y)}{\text{outdeg}(y)}\]

corresponding to the intuitive equations given in (\ref{20.2.1}). These numbers must also satisfy the additional constraint corresponding to (\ref{20.2.2}):

\[\label{20.2.4} \sum_{\text{vertices } x} \text{Rank}(x) = 1.\]

So if there are n vertices, then equations (\ref{20.2.3}) and (\ref{20.2.4}) provide a system of \(n + 1\) linear equations in the n variables, \(\text{Rank}(x)\). Note that constraint (\ref{20.2.4}) is needed because the remaining constraints (\ref{20.2.3}) could be satisfied by letting \(\text{Rank}(x) ::= 0\) for all \(x\), which is useless.

Sergey and Larry were smart fellows, and they set up their page rank algorithm so it would always have a meaningful solution. Strongly connected graphs have unique stationary distributions (Problem 20.12), and their addition of a supervertex ensures this. Moreover, starting from any vertex and taking a sufficiently long random walk on the graph, the probability of being at each page will get closer and closer to the stationary distribution. Note that general digraphs without super-vertices may have neither of these properties: there may not be a unique stationary distribution, and even when there is, there may be starting points from which the probabilities of positions during a random walk do not converge to the stationary distribution (Problem 20.8).

Now just keeping track of the digraph whose vertices are trillions of web pages is a daunting task. That’s why in 2011 Google invested $168,000,000 in a solar power plant—the electrical power drawn by Google’s servers in 2011 would have supplied the needs of 200,000 households.³ Indeed, Larry and Sergey named their system Google after the number \(10^{100}\)—which is called a “googol”—to reflect the fact that the web graph is so enormous.

Anyway, now you can see how this text ranked first out of 378,000 matches. Lots of other universities used our notes and presumably have links to the MIT Mathematics for Computer Science Open Course Ware site, and the university sites themselves are legitimate, which ultimately leads to the text getting a high page rank in the web graph.

²First rank for some reason was an early version archived at Princeton; the Spring 2010 version on the MIT Open Courseware site ranked 4th and 5th.

³Google Details, and Defends, Its Use of Electricity, New York Times, September 8, 2011.