3.1: Voltage, Current, and Generic Circuit Elements
- Page ID
- 1606
- Learn about various signals such as voltage and current.
- Systems which are used to manipulate signals are called circuits.
We know that information can be represented by signals; now we need to understand how signals are physically realized. Over the years, electric signals have been found to be the easiest to use. Voltage and currents comprise the electric instantiations of signals. Thus, we need to delve into the world of electricity and electromagnetism. The systems used to manipulate electric signals directly are called circuits, and they refine the information representation or extract information from the voltage or current. In many cases, they make nice examples of linear systems.
A generic circuit element places a constraint between the classic variables of a circuit: voltage and current. Voltage is electric potential and represents the "push" that drives electric charge from one place to another. What causes charge to move is a physical separation between positive and negative charge. A battery generates, through electrochemical means, excess positive charge at one terminal and negative charge at the other, creating an electric field. Voltage is defined across a circuit element, with the positive sign denoting a positive voltage drop across the element. When a conductor connects the positive and negative potentials, current flows, with positive current indicating that positive charge flows from the positive terminal to the negative. Electrons comprise current flow in many cases. Because electrons have a negative charge, electrons move in the opposite direction of positive current flow: Negative charge flowing to the right is equivalent to positive charge moving to the left.
It is important to understand the physics of current flow in conductors to appreciate the innovation of new electronic devices. Electric charge can arise from many sources, the simplest being the electron. When we say that "electrons flow through a conductor," what we mean is that the conductor's constituent atoms freely give up electrons from their outer shells. "Flow" thus means that electrons hop from atom to atom driven along by the applied electric potential. A missing electron, however, is a virtual positive charge. Electrical engineers call these holes, and in some materials, particularly certain semiconductors, current flow is actually due to holes. Current flow also occurs in nerve cells found in your brain. Here, neurons "communicate" using propagating voltage pulses that rely on the flow of positive ions (potassium and sodium primarily, and to some degree calcium) across the neuron's outer wall. Thus, current can come from many sources, and circuit theory can be used to understand how current flows in reaction to electric fields.
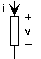
Current flows through circuit elements, such as that depicted in the figure above, and through conductors, which we indicate by lines in circuit diagrams. For every circuit element we define a voltage and a current. The element has a v-i relation defined by the element's physical properties. In defining the v-i relation, we have the convention that positive current flows from positive to negative voltage drop. Voltage has units of volts, and both the unit and the quantity are named for Volta. Current has units of amperes, and is named for the French physicist Ampère.
Voltages and currents also carry power. Again using the convention shown in Figure 3.1.1 for circuit elements, the instantaneous power at each moment of time consumed by the element is given by the product of the voltage and current.
\[p(t) = v(t)i(t) \nonumber \]
A positive value for power indicates that at time
\[E(t) = \int_{-\infty }^{t}p(\alpha )d\alpha \nonumber \]
Again, positive energy corresponds to consumed energy and negative energy corresponds to energy production. Note that a circuit element having a power profile that is both positive and negative over some time interval could consume or produce energy according to the sign of the integral of power. The units of energy are joules since a watt equals joules/second.
Residential energy bills typically state a home's energy usage in kilowatt-hours. Is this really a unit of energy? If so, how many joules equals one kilowatt-hour?
Solution
One kilowatt-hour equals 3,600,000 watt-seconds, which indeed directly corresponds to 3,600,000 joules.


