4.8: Derivation of the Fourier Transform
- Page ID
- 1800
- This module shows how to derive the scintillating and useful Fourier transform.
Fourier series clearly open the frequency domain as an interesting and useful way of determining how circuits and systems respond to periodic input signals. Can we use similar techniques for nonperiodic signals? What is the response of the filter to a single pulse? Addressing these issues requires us to find the Fourier spectrum of all signals, both periodic and nonperiodic ones. We need a definition for the Fourier spectrum of a signal, periodic or not. This spectrum is calculated by what is known as the Fourier transform.
Let sT(t) be a periodic signal having period T. We want to consider what happens to this signal's spectrum as we let the period become longer and longer. We denote the spectrum for any assumed value of the period by ck(T). We calculate the spectrum according to the familiar formula:
\[c_{k}(T)=\frac{1}{2}\int_{-\frac{T}{2}}^{\frac{T}{2}}s_{T}(t)e^{-i\frac{2\pi kt}{T}}dt \nonumber \]
where we have used a symmetric placement of the integration interval about the origin for subsequent derivational convenience. Let f be a fixed frequency equaling k/T; we vary the frequency index k proportionally as we increase the period. Define
\[S_{T}(f)\equiv Tc_{k}(T)=\frac{1}{2}\int_{-\frac{T}{2}}^{\frac{T}{2}}s_{T}(t)e^{-i2\pi kt}dt \nonumber \]
making the corresponding Fourier series
\[s_{T}(t)=\sum_{k=-\infty }^{\infty }S_{T}(f)e^{i2\pi ft}\frac{1}{T} \nonumber \]
As the period increases, the spectral lines become closer together, becoming a continuum. Therefore,
\[\lim_{T \to \infty}s_{T}(t)\equiv s(t)=\int_{-\infty }^{\infty }S(f)e^{i2\pi ft}df \nonumber \]
where
\[S(f)= \int_{-\infty }^{\infty }s(t)e^{-(i2\pi ft)}dt \nonumber \]
S(f) S(f) is the Fourier transform of s(t) (the Fourier transform is symbolically denoted by the uppercase version of the signal's symbol) and is defined for any signal for which the integral converges.
Let's calculate the Fourier transform of the pulse signal, p(t).
\[P(f)=\int_{-\infty }^{\infty }p(t)e^{-(i2\pi ft)}dt=\int_{0}^{\Delta }e^{-(i2\pi ft)}dt=\frac{1}{-(i2\pi f)}\left ( e^{-(i2\pi f\Delta )} -1\right ) \nonumber \]
\[P(f)=e^{-(i2\pi f\Delta )}\frac{\sin (\pi f\Delta )}{\pi f} \nonumber \]
Note how closely this result resembles the expression for Fourier series coefficients of the periodic pulse signal.

Figure 4.8.1 shows how increasing the period does indeed lead to a continuum of coefficients, and that the Fourier transform does correspond to what the continuum becomes. The quantity
\[\frac{\sin (t)}{t} \nonumber \]
has a special name, the sinc (pronounced "sink") function, and is denoted by sinc(t). Thus, the magnitude of the pulse's Fourier transform equals
\[\left | \Delta sinc (\pi f\Delta ) \right | \nonumber \]
The Fourier transform relates a signal's time and frequency domain representations to each other. The direct Fourier transform (or simply the Fourier transform) calculates a signal's frequency domain representation from its time-domain variant. See equation below. The inverse Fourier transform (Equation) finds the time-domain representation from the frequency domain. Rather than explicitly writing the required integral, we often symbolically express these transform calculations as
\[\mathfrak{F}(s)\; \; and\; \; \mathfrak{F}^{-1}(S) \nonumber \]
respectively.
\[\mathfrak{F}(s)=S(f)=\int_{-\infty }^{\infty }s(t)e^{-(i2\pi ft)}dt \nonumber \]
\[\mathfrak{F}^{-1}(s)=s(t)=\int_{-\infty }^{\infty }S(f)e^{i2\pi ft}df \nonumber \]
We must have
\[s(t)=\mathfrak{F}^{-1}(\mathfrak{F(s(t))}) \nonumber \]
\[S(f)=\mathfrak{F}(\mathfrak{F}^{-1}(S(f))) \nonumber \]
These results are indeed valid with minor exceptions.
Recall that the Fourier series for a square wave gives a value for the signal at the discontinuities equal to the average value of the jump. This value may differ from how the signal is defined in the time domain, but being unequal at a point is indeed minor.
Showing that you "get back to where you started" is difficult from an analytic viewpoint, and we won't try here. Note that the direct and inverse transforms differ only in the sign of the exponent.
The differing exponent signs means that some curious results occur when we use the wrong sign. What is \[\mathfrak{F}(S(f)) \nonumber \]
In other words, use the wrong exponent sign in evaluating the inverse Fourier transform.
Solution
\[\mathfrak{F}(S(f))=\int_{-\infty }^{\infty }S(f)e^{-(i2\pi ft)}df=\int_{-\infty }^{\infty }S(f)e^{i2\pi f(-t)}df=s(-t) \nonumber \]
Properties of the Fourier transform and some useful transform pairs are provided in the accompanying tables. Especially important among these properties is Parseval's Theorem, which states that power computed in either domain equals the power in the other.
\[\int_{-\infty }^{\infty }s^{2}(t)dt=\int_{-\infty }^{\infty }\left ( \left | S(f) \right | \right )^{2}df \nonumber \]
Of practical importance is the conjugate symmetry property: When s(t) is real-valued, the spectrum at negative frequencies equals the complex conjugate of the spectrum at the corresponding positive frequencies. Consequently, we need only plot the positive frequency portion of the spectrum (we can easily determine the remainder of the spectrum).
How many Fourier transform operations need to be applied to get the original signal back:
\[\mathfrak{F}(...(\mathfrak{F}(s)))=s(t) \nonumber \]
Solution
\[\mathfrak{F}(\mathfrak{F}(\mathfrak{F}(\mathfrak{F}(s(t)))))=s(t) \nonumber \]
We know that
\[\mathfrak{F}(S(f))=\int_{-\infty }^{\infty }S(f)e^{-(i2\pi ft)}df=\int_{-\infty }^{\infty }S(f)e^{i2\pi f(-t)}df=s(-t) \nonumber \]
Therefore, two Fourier transforms applied to s(t) yields s(-t). We need two more to get us back where we started.
Note that the mathematical relationships between the time domain and frequency domain versions of the same signal are termed transforms. We are transforming (in the nontechnical meaning of the word) a signal from one representation to another. We express Fourier transform pairs as:
\[s(t)\leftrightarrow S(f) \nonumber \]
A signal's time and frequency domain representations are uniquely related to each other. A signal thus "exists" in both the time and frequency domains, with the Fourier transform bridging between the two. We can define an information carrying signal in either the time or frequency domains; it behooves the wise engineer to use the simpler of the two.
A common misunderstanding is that while a signal exists in both the time and frequency domains, a single formula expressing a signal must contain only time or frequency: Both cannot be present simultaneously. This situation mirrors what happens with complex amplitudes in circuits: As we reveal how communications systems work and are designed, we will define signals entirely in the frequency domain without explicitly finding their time domain variants. This idea is shown in another module where we define Fourier series coefficients according to letter to be transmitted. Thus, a signal, though most familiarly defined in the time-domain, really can be defined equally as well (and sometimes more easily) in the frequency domain. For example, impedances depend on frequency and the time variable cannot appear.
We will learn that finding a linear, time-invariant system's output in the time domain can be most easily calculated by determining the input signal's spectrum, performing a simple calculation in the frequency domain, and inverse transforming the result. Furthermore, understanding communications and information processing systems requires a thorough understanding of signal structure and of how systems work in both the time and frequency domains.
The only difficulty in calculating the Fourier transform of any signal occurs when we have periodic signals (in either domain). Realizing that the Fourier series is a special case of the Fourier transform, we simply calculate the Fourier series coefficients instead, and plot them along with the spectra of nonperiodic signals on the same frequency axis.
In communications, a very important operation on a signal s(t) is to amplitude modulate it. Using this operation more as an example rather than elaborating the communications aspects here, we want to compute the Fourier transform — the spectrum — of
\[(1+s(t))\cos (2\pi f_{c}t) \nonumber \]
Thus,
\[(1+s(t))\cos (2\pi f_{c}t)=\cos (2\pi f_{c}t)+s(t)\cos (2\pi f_{c}t) \nonumber \]
For the spectrum of cos(2πfct), we use the Fourier series. Its period is 1/fc, and its only nonzero Fourier coefficients are c+1=1/2. The second term is not periodic unless s(t) has the same period as the sinusoid. Using Euler's relation, the spectrum of the second term can be derived as
\[s(t)\cos (2\pi f_{c}t)=\int_{-\infty }^{\infty }S(f)e^{i2\pi ft}df\cos (2\pi f_{c}t) \nonumber \]
Using Euler's relation for the cosine,
\[s(t)\cos (2\pi f_{c}t)=\frac{1}{2}\int_{-\infty }^{\infty }S(f)e^{i2\pi (f+f_{c})t}df+\frac{1}{2}\int_{-\infty }^{\infty }S(f)e^{i2\pi (f-f_{c})t}df \nonumber \]
\[s(t)\cos (2\pi f_{c}t)=\frac{1}{2}\int_{-\infty }^{\infty }S(f-f_{c})e^{i2\pi ft}df+\frac{1}{2}\int_{-\infty }^{\infty }S(f+f_{c})e^{i2\pi ft}df \nonumber \]
\[s(t)\cos (2\pi f_{c}t)=\int_{-\infty }^{\infty }\frac{S(f-f_{c})+S(f+f_{c})}{2}e^{i2\pi ft}df \nonumber \]
Exploiting the uniqueness property of the Fourier transform, we have
\[\mathfrak{F}(s(t)\cos (2\pi f_{c}t))=\frac{S(f-f_{c})+S(f+f_{c})}{2} \nonumber \]
This component of the spectrum consists of the original signal's spectrum delayed and advanced in frequency. The spectrum of the amplitude modulated signal is shown in Figure4.8.2.
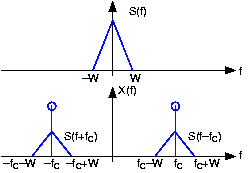
Note how in this figure the signal s(t) is defined in the frequency domain. To find its time domain representation, we simply use the inverse Fourier transform.
What is the signal s(t) that corresponds to the spectrum shown in the upper panel of Figure 4.8.2?
Solution
The signal is the inverse Fourier transform of the triangularly shaped spectrum, and equals:
\[s(t)=W\left ( \frac{\sin (\pi W_{t})}{\pi W_{t}} \right )^{2} \nonumber \]
What is the power in x(t), the amplitude-modulated signal? Try the calculation in both the time and frequency domains.
Solution
The result is most easily found in the spectrum's formula: the power in the signal-related part of x(t) is half the power of the signal s(t).
In this example, we call the signal s(t) a baseband signal because its power is contained at low frequencies. Signals such as speech and the Dow Jones averages are baseband signals. The baseband signal's bandwidth equals W, the highest frequency at which it has power. Since x(t)'s spectrum is confined to a frequency band not close to the origin (we assume fc»W), we have a bandpass signal. The bandwidth of a bandpass signal is not its highest frequency, but the range of positive frequencies where the signal has power. Thus, in this example, the bandwidth is 2W Hz. Why a signal's bandwidth should depend on its spectral shape will become clear once we develop communications systems.


