7.4: Ampere’s Circuital Law (Magnetostatics) - Integral Form
- Page ID
- 3940
Ampere’s circuital law (ACL) relates current to the magnetic field associated with the current. In the magnetostatic regime, the law is (see also Figure \(\PageIndex{1}\)):
\[\boxed{ \oint_{\mathcal C}{ {\bf H} \cdot d{\bf l} } = I_{encl} } \label{m0019_eACL} \]
That is, the integral of the magnetic field intensity \({\bf H}\) over a closed path \({\mathcal C}\) is equal to the current enclosed by that path, \(I_{encl}\). Before proceeding to interpret this law, it is useful to see that it is dimensionally correct. That is, \({\bf H}\) (units of A/m) integrated over a distance (units of m) yields a quantity with units of current (i.e., A).
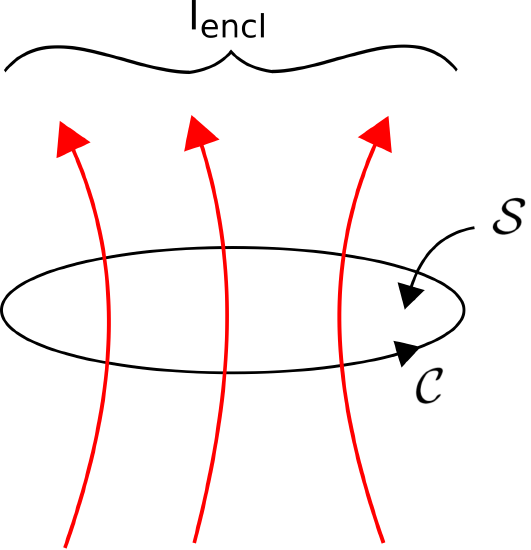
In general, \(I_{encl}\) may be either positive or negative. The direction corresponding to positive current flow must be correctly associated with \({\mathcal C}\). The relationship follows the right-hand rule of Stokes’ Theorem summarized as follows. The direction of positive \(I_{encl}\) is the direction in which the fingers of the right hand intersect any surface \({\mathcal S}\) bordered by \({\mathcal C}\) when the thumb of the right hand points in the direction of integration. The connection to Stokes’ Theorem is not a coincidence. See Section 7.9 for more about this.
Note that \({\mathcal S}\) can be any surface that is bounded by \({\mathcal C}\) – not just the taut surface implied in Figure \(\PageIndex{1}\).
The integral form of Ampere’s Circuital Law for magnetostatics (Equation \ref{m0019_eACL}) relates the magnetic field along a closed path to the total current flowing through any surface bounded by that path.
ACL plays a role in magnetostatics that is very similar to the role played by the integral form of Gauss’ Law in electrostatics (Section 5.5). That is, ACL provides a means calculate the magnetic field given the source current. ACL also has a similar limitation. Generally, symmetry is required to simplify the problem sufficiently so that the integral equation may be solved. Fortunately, a number of important problems fall in this category. Examples include the problems addressed in Sections 7.5 (magnetic field of a line current), 7.6 (magnetic field inside a straight coil), 7.7 (magnetic field of a toroidal coil), 7.8 (magnetic field of a current sheet), and 7.11(boundary conditions on the magnetic field intensity). For problems in which the necessary symmetry is not available, the differential form of ACL may be required (Section 7.9).
Finally, be aware that the form of ACL addressed here applies to magnetostatics only. In the presence of a time-varying electric field, the right side of ACL includes an additional term known as the displacement current (Section 8.9).


