The Cooley-Tukey FFT always uses the Type 2 index map from Multidimensional Index Mapping. This is necessary for the most popular forms that have \(N=R^M\), but is also used even when the factors are relatively prime and a Type 1 map could be used. The time and frequency maps from Multidimensional Index Mapping are
\[n=((K_1n_1+K_2n_2))_N \nonumber \]
\[k=((K_3k_1+K_4k_2))_N \nonumber \]
Type-2 conditions in the 2.2: The Index Map become
\[K_1=aN_2\; \; or\; \; K_2=bN_1\; \; but\; not\; both \nonumber \]
and
\[K_3=cN_2\; \; or\; \; K_4=dN_1\; \; but\; not\; both \nonumber \]
The row and column calculations in 2.2: The Index Map are uncoupled by Type-two index map which for this case are
\[((K_1K_4))_N=0\; \; or\; \; ((K_2K_3))_N=0\; \; but\; not\; both \nonumber \]
To make each short sum a DFT, the KiKi" role="presentation" style="position:relative;" tabindex="0">\(K_i\) must satisfy
\[((K_1K_3))_N=N_2\; \; and\; \; ((K_2K_4))_N=N_1 \nonumber \]
In order to have the smallest values for KiKi" role="presentation" style="position:relative;" tabindex="0">\(K_i\) the constants in the equation are chosen to be
\[a=d=K_2=K_3=1 \nonumber \]
which makes the index maps of the equations to become
\[n=N_2n_1+n_2 \nonumber \]
\[k=k_1+N_1k_2 \nonumber \]
These index maps are all evaluated modulo \(N\), but in the equation, explicit reduction is not necessary since \(n\) never exceeds \(N\). The reduction notation will be omitted for clarity. From Multidimensional Index Mapping, the DFT is
\[X=\sum_{n_2=0}^{N_2-1}\sum_{n_1=0}^{N_1-1}xW_{N_1}^{n_1k_1}W_{N}^{n_2k_1}W_{N_2}^{n_2k_2} \nonumber \]
This map of the equation and the form of the DFT in the equation are the fundamentals of the Cooley-Tukey FFT.
The order of the summations using the Type 2 map in the above equation cannot be reversed as it can with the Type-1 map. This is because of the \(W_N\) terms, the twiddle factors.
Turning the equation into an efficient program requires some care. From Efficiencies Resulting from Index Mapping with the DFT we know that all the factors should be equal. If \(N=R^M\), with R called the radix, \(N_1\)is first set equal to \(R\) and \(N_2\) is then necessarily \(R^{M-1}\). Consider \(n_1\) to be the index along the rows and \(n_2\)along the columns. The inner sum of the equation over \(n_1\) represents a length-\(N_1\) DFT for each value of \(n_2\). These \(N_2\) length-\(N_1\) DFT's are the DFT's of the rows of the \(x(n_1,n_2)\) array. The resulting array of row DFT's is multiplied by an array of twiddle factors which are the \(W_N\) terms inthe equation. The twiddle-factor array for a length-8 radix-2 FFT is
\[TF:W_{8}^{n_2k_1}=\begin{bmatrix} W^0 & W^0\\ W^0 & W^1\\ W^0 & W^2\\ W^0 & W^3 \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 1 & W\\ 1 & -j\\ 1 & -jW \end{bmatrix} \nonumber \]
The twiddle factor array will always have unity in the first row and first column.
To complete the equation at this point, after the row DFT's are multiplied by the TF array, the \(N_1\) length-\(N_2\) DFT's of the columns are calculated. However, since the columns DFT's are of length \(R^{M-1}\), they can be posed as a \(R^{M-2}\) by \(R\) array and the process repeated, again using length-\(R\) DFT's. After \(M\) stages of length-\(R\) DFT's with TF multiplications interleaved, the DFT is complete. The flow graph of a length-2 DFT is given in Fig. 8.2.1 and is called a butterfly because of its shape. The flow graph of the complete length-8 radix-2 FFT is shown in Fig. 8.2.2.
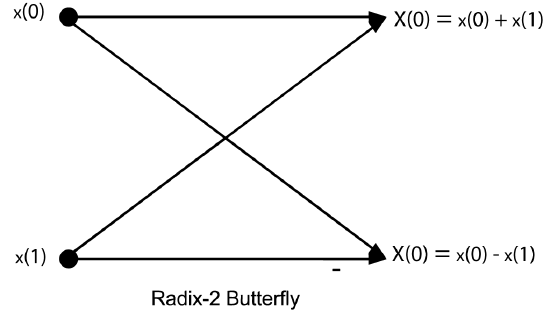
Fig. 8.2.1 A Radix-2 Butterfly
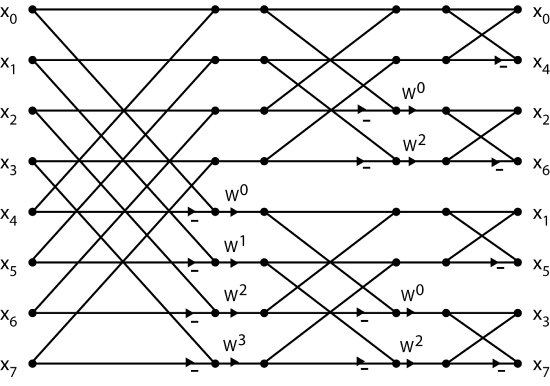
Fig. 8.2.2 Length-8 Radix-2 FFT Flow Graph
This flow-graph, the twiddle factor map of the above equation, and the basic equation should be completely understood before going further.
A very efficient indexing scheme has evolved over the years that results in a compact and efficient computer program. A FORTRAN program is given below that implements the radix-2 FFT. It should be studied to see how it implements equation and the flow-graph representation.
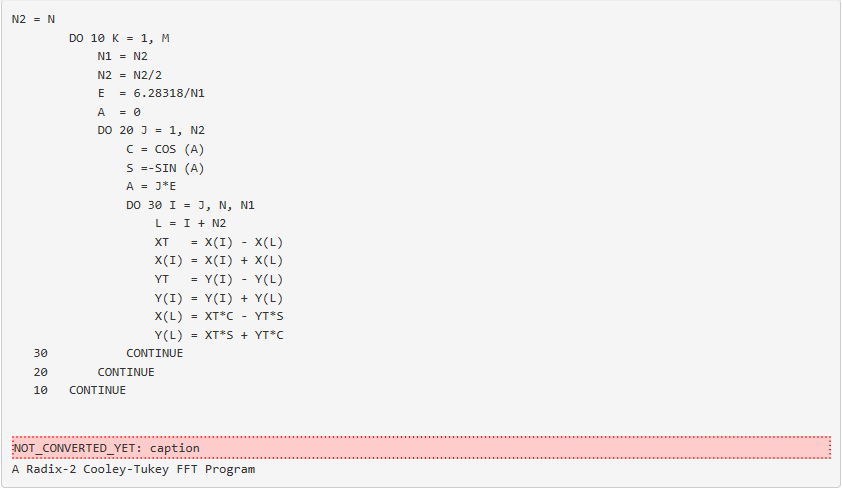
This discussion, the flow graph of Winograd's Short DFT Algorithms and the program of Pre are all based on the input index map of The Index Map and the calculations are performed in-place. According to In-Place Calculation of the DFT and Scrambling, this means the output is scrambled in bit-reversed order and should be followed by an unscrambler to give the DFT in proper order. This formulation is called a decimation-in-frequency FFT. A very similar algorithm based on the output index map can be derived which is called a decimation-in-time FFT. Examples of FFT programs are found in the Appendix of this book.





