4.16: Problems

For Section 4.3:

Prob. 4.3.1

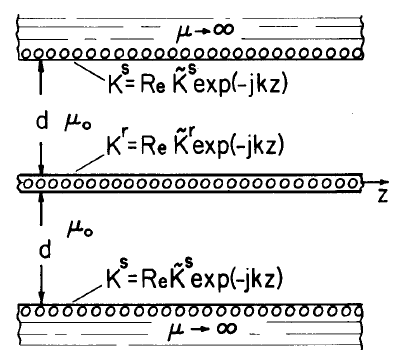
The cross section of a "double-sided machine"is shown in Fig. P4.3.1. The "rotor" is modeled as current sheet.

(a) Find the force \(f_z\), acting in the \(z\) direction on an area \(A\) of the sheet.

(b) Now take the excitations as given by Eqs. 4.3.5a and 4.3.6a for synchronous interactions and evaluate \(f_z\).

(c) For a d-c interaction, the excitations are given by Eqs. 4.3.10a. Find \(f_z\).

Fig. P4.3.1

Prob. 4.3.2

The developed model for a "trapped flux"synchronous machine is shown in Fig. P4.3.2. (See case 3a of Table 4.3.1). Te stator surface current is specified as in Eq. 4.3.6a. The "rotor" consists of a perfectly conducting material. When \(t=0\), the currents in this material have a pattern such that the flux normal to the rotor surface is \(B_x^r = B^r_o cos \, k [Ut-(z-\delta)]\), where \(U\) is the velocity of the rotor. Find \(f_z\) first in terms of \(\tilde{K}^s\) and \(\tilde{B}^r\) and then in terms of \(K^s_o\) and \(B^r_o\).In practice, such a synchronous force would exist as a transient provided the initial current distribution diffused away, as described in Sec. 6.6, on a time scale long compared to that of interest.

Fig. P4.3.2

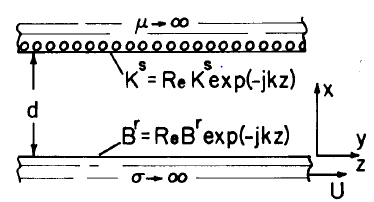
Prob. 4.3.3

The moving member of an EQS device takes the form of a sheet, supporting the surface charge af and moving in the \(z\) direction, as shown in Fig. P4.3.3. Electrodes on the adjacent walls constrain the potentials there.

a) Find the force \(f_z\), on an area \(A\) of the sheet in terms of \((\hat{\phi}^a, \hat{\sigma}_f, \hat{\phi}^b)\).

(b) For a synchronous interaction, \(\omega/k = U\). The surface charge is given by \(-\sigma_o \, cos \, [\omega t - k(z-\delta)]\) and \( \phi^a = V_o \, cos \, (\omega t - kz)\). For even excitations \(\phi^b = \phi^a\). Find \(f_z\)

(c) An example of a d-c interaction is the Van de Graaf machine taken up in Sec. 4.14. With the excitations \(\phi^a = \phi^b = - V_o \, cos \, kz\) and \(\sigma_f = \sigma_o \, sin \, kz\). find \(f_z\).

Fig. P4.3.3

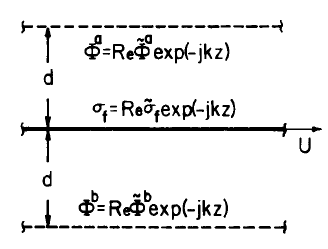
For Section 4.4:

Prob. 4.4.1

This problem is intended to give the opportunity to follow through the approach to developing a lumped parameter model illustrated in Sec. 4.4. However, for best efficiency in determining the electrical terminal relations, it will be helpful to use the transfer relations of Sec. 2.19, and study of Sec. 4.7 is recommended in this regard.

The cross section of a model for a permanent-magnetization rotating magnetic machine is shown in Fig. P4.4.1. The magnetization density in the rotor is uniform and of magnitude \(M_o\).The stator is wound with a uniform turn density \(N\), so that the surface current density over \(2 \theta_o\), the span of the turns, is \(Ni(t)\).

(a) Show that in the rotor volume, \(\overrightarrow{B}\) is both solenoidal and irrotational so that the transfer relations of Table 2.19.1 apply provided that pH0 is taken as \(B_{\theta}\).

(b) Show that boundary conditions at the rotor interface implied by the divergence condition on \(\overrightarrow{B}\) and Ampere's law are

\[ \overrightarrow{n} \cdot [] \overrightarrow{B} [] = 0; \quad \overrightarrow{n} \times [] B [] = \mu_o \overrightarrow{K}_f + \mu_o \overrightarrow{n} \times [] \overrightarrow{M} [] \nonumber \]

(c) Find the instantaneous torque on the rotor as a function of \((\theta_r,i)\). (Your result should be analogous to Eq. 4.4.11.)

(d) Find the electrical terminal relation \(\lambda(\theta_r,i,M_o)\). (This result is analogous to Eq. 4.4.14.)

Fig. P4.4.1

For Section 4.6:

Prob. 4.6.1

A charged particle beam takes the form of a planar layer moving in the z direction with the velocity \(U\), as shown in Fig. P4.6.1. The charge density within the beam is

\[ \rho = Re \, \tilde{\rho}_o \, e^{-jkz} \nonumber \]

Thus the density is uniform in the x direction within the beam, i.e., in the region \(-b/2 < x< b/2\). The walls, which are constrained in potential as shown, are separated from the beam by planar regions of free space of thickness \(d\).

(a) In terms of the complex functions of time \(\tilde{V}_o\) and \(\tilde{\rho}_o\),find the electrical force acting on an area \(A\) (in the y-z plane) of the beam in the \(z\) direction.

(b) Now, specialize the analysis by letting

\[ \phi^a = \phi^f = V_o \, cos(\omega t - kz) \nonumber \]

\[ \rho = - \rho_o \, cos [\omega t - k(z - \delta)] \nonumber \]

Given that the charged particles comprising the beam move with velocity \(U\), and that \(k\) is specified what is \(\omega\)? Evaluate the force found in (a) in terms of the phase displacement 6 and the amplitudes \(V_o\) and \(\rho_o\).

(c) Now consider the same problem from another viewpoint. Consider the entire region \(-(d+ \frac{b}{2})< x < (d+ \frac{b}{2})\) as one region and find alternative expressions for parts (a) and (b).

For Section 4.8:

Prob. 4.8.1

Transfer relations are developed here that are the Cartesian coordinate analogues of those in Sec. 4.8.

(a) With variables taking the form \(A = Re \, \tilde{A}(x,t) \, e^{-jky} \) and \(H_y = Re \, \tilde{H}_y(x,t) \, e^{-jky}\) and a volume current density (in the z direction) \(J = Re \, \tilde{J} (x,t) \, e^{-jky} \), start with Eq. (b) of Table 2.19.1 and show that the transfer relations take the form

\[ \begin{bmatrix} \tilde{A}^{\alpha} \\ \tilde{A}^{\beta} \end{bmatrix} \nonumber \]

(b) The bulk current density and particular solution for \(A\) are represented in terms of modes \(\Pi_i(x)\):

\[ J = Re \, \Sigma_{i=0}^{\infty} \, \tilde{J}_i (t) \Pi_i(x) \, e^{-jky} \, ; \quad A_p = Re \, \Sigma_{i=0}^{\infty} \, \tilde{A}_i(t) \Pi_i(x) \, e^{-jky} \nonumber \]

Show that if the modes are required to have zero derivatives at the surfaces,the transfer relations become

\[ \begin{bmatrix} \tilde{A}^{\alpha} \\ \tilde{A}^{\beta} \end{bmatrix} = \frac{\mu}{k} \begin{bmatrix} -coth \, k \Delta & \frac{1}{sinh \, k \Delta} \\ \frac{-1}{sinh \, k \Delta} & coth \, k \Delta \end{bmatrix} \begin{bmatrix} \tilde{H}_y^{\alpha} \\ \tilde{H}_y^{\beta} \end{bmatrix} + \Sigma_{i=0}^{\infty} \frac{\mu \tilde{J}_i}{(\frac{i \pi}{\Delta})^2 + k^2} \, \begin{bmatrix} (-1)^{i} \\ 1 \end{bmatrix} \nonumber \]

\[\begin{bmatrix} \tilde{\phi}^{\alpha}\\ \tilde{\phi}^{\beta} \end{bmatrix} = \begin{bmatrix} -A_{11} & -A_{12} \\ -A_{21} & -A_{22} \end{bmatrix} \begin{bmatrix} \tilde{D}_n^{\alpha}\\ \tilde{D}_n^{\beta} \end{bmatrix} \label{6} \]