7.5: Problems
- Page ID
- 18983
7.1. Identify whether the devices below operate based on spontaneous emission, stimulated emission, or absorption.
- Light emitting diode
- Gas discharge lamp
- Argon ion laser
- Solar panel
- Semiconductor laser
7.2. Consider a blackbody radiator at a temperature of 6500 K. Use Matlab, or similar software, to answer this question.
(a) Find the frequency which corresponds to peak spectral energy density per unit bandwidth.
(b) Find the wavelength which corresponds to peak spectral energy density per unit bandwidth.
(c) Find the value of the spectral energy density per unit bandwidth in \(\frac{J \cdot s}{m^3}\) at the frequency found in part \(a\).
7.3. A semiconductor laser which emits \(\lambda = 500\) nm light has a length of \(800 \mu m\). The width is \(12 \mu m\), and the thickness is \(5 \mu m\). How many wavelengths long is the device in the longitudinal direction? How many wavelengths long is the device in each transverse direction?
7.4. Assume a semiconductor laser has a length of \(800 \mu m\). Laser emission can occur when the cavity length is equal to an integer number of half wavelengths. What wavelengths in the range 650 nm \(< \lambda <\) 652 nm can this laser emit, and in each case, list the cavity length in wavelengths.
7.5. Assume two energy levels of a gas laser are separated by 1.4 eV, and assume that they are equally degenerate (\(g_1 = g_2\)). The spontaneous emission Einstein coecient for transitions between these energy levels is given by \(A_{12} = 3 \cdot 10^6 s^{-1}\). Find the other two Einstein coefficients, \(B_{12}\) and \(B_{21}\).
7.6. The energy gap of AlAs is 2.3 eV, and the energy gap of AlSb is 1.7 eV [9, p. 19]. Energy gaps of materials of composition AlAs\(_x\)Sb\(_{1−x}\) with \(0 \leq x \leq 1\) vary approximately linearly between these values [9, p. 19]. Suppose you would like to make a semiconductor laser from a material of composition AlAs\(_x\)Sb\(_{1−x}\). Find the value of \(x\) that specifies the composition of a material which emits light at wavelength \(\lambda = 640\) nm.
7.7. Laser spectra are often modeled by Lorentzian functions. A Lorentzian function centered at the origin with area under the curve of unity has equation
\[y(x) = \frac{1}{\pi} \cdot \frac{0.5 \cdot \mathrm{FWHM}}{x^2 + (0.5 \cdot \mathrm{FWHM})^2}\nonumber \]
where FWHM is the full width at half maximum. The maximum value of this function is \(\frac{2}{\pi \cdot \mathrm{FWHM}}\). The laser spectrum of Fig. 7.7 is centered near \(\lambda = 570\) nm, has a FWHM of 5 nm, and it has a maximum luminescence intensity of 49. Find a Lorentzian equation that can model this particular spectrum.
7.8. As discussed in the previous problem, laser spectra are often modeled by Lorentzian functions. To better understand Lorentzian functions, use Matlab or similar software for this problem.
(a) Plot a Lorentzian function centered at the origin with FWHM 5 and maximum amplitude of unity. On the same axis, plot a Gaussian function also centered at the origin with FWHM 5 and maximum amplitude of unity.
(b) Repeat part a, but put the vertical axis of your plots on a log scale.
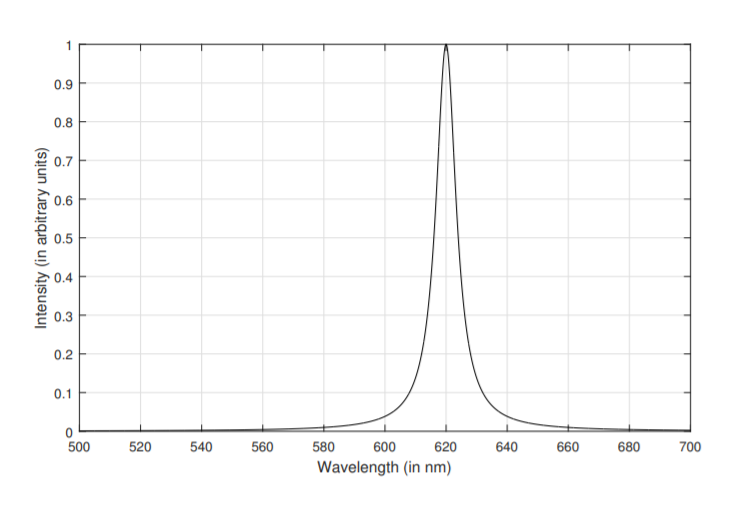
7.9. The figure illustrates a laser spectrum. Approximately find:
(a) The wavelength of peak intensity
(b) The FWHM
(c) The quality factor
7.10. Three main components of a laser are the pump, active material, and cavity. Four main types of lasers are gas lasers, semiconductor lasers, dye lasers, and solid state lasers. Match the example component with the best description of the type of component and type of laser it is found in specified. (Each answer will be used once.)
| Example Component |
|---|
| 1. Edges of a AlGaAs crystal |
| 2. Rhodamine 6G liquid solution |
| 3. External mirror made of SiO2 glass coated with aluminum |
| 4. Battery of a laser pointer |
| 5. SiO2 glass doped with 1% Er atoms |
| 6. CO2 gas in an enclosed tube |
| 7. Pn junction made from InGaAs |
| 8. Argon ion laser used to supply energy to excite electrons of a Ti doped Sapphire |
| Description |
|---|
| A. Cavity of a semiconductor laser |
| B. Cavity of a gas laser |
| C. Active material of a semiconductor laser |
| D. Active material of a gas laser |
| E. Active material of a dye laser |
| F. Active material of a solid state laser |
| G. Pump of a semiconductor laser |
| H. Pump of a solid state laser |
7.11. The intensity from sunlight on a bright sunny day is around \(0.1 \frac{W}{cm^2}\). Laser power can be confined to a very small spot size. Assume a laser produces a beam with spot size 1 \(mm^2\). For what laser power in watts will the intensity of the beam be equivalent to the intensity from sunlight on sunny day? Staring at the sun can damage an eye, so staring at a laser beam of this intensity is dangerous for the same reason.


