10.5: Electrofluidics
- Page ID
- 19039
Electrohydrodynamic devices (EHDs) convert between electrical energy and fluid flow. These devices are also known as electrokinetic devices. Microfluidic devices are EHD devices that are patterned on a single silicon wafer or other substrate, and length scales are often less than a millimeter [159]. Engineers have built EHD pumps, valves, mixers, separators, and other EHD devices [159] [160]. Electrohydrodynamic or microfluidic devices have been used in products including ink jet printers, chemical detectors, machines for DNA sequencing or protein analysis, and insulin pumps [61] [160] [161].
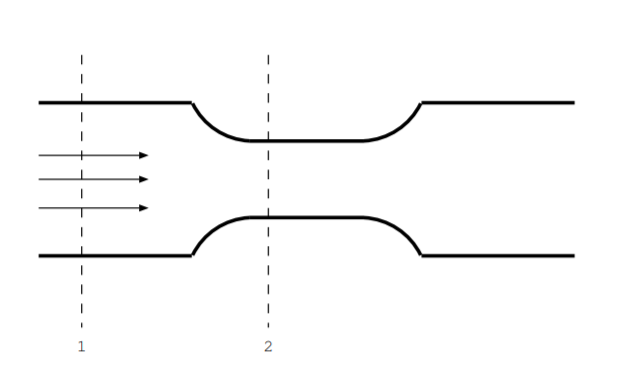
Some EHD devices operate based on the idea of Bernoulli's equation, and this relationship is a direct consequence of energy conservation. To illustrate the fundamental physics of this idea, begin by considering a simpler device, a constricted pipe. This pipe converts energy from a pressure differential to kinetic energy [103, ch. 3] [162, p. 346]. Consider a fluid with zero viscosity and zero thermal conductivity flowing through a horizontal pipe (so gravity can be ignored). Figure \(\PageIndex{1}\) illustrates this geometry. The velocity \(\overrightarrow{v}\) and pressure \(\mathbb{P}\) are different at locations with different pipe diameter, for example locations 1 and 2 in the figure. Consider a small amount of water with mass \(m = \rho_{dens} \Delta \mathbb{V}\) where \(\rho_{dens}\) is density and \(\Delta \mathbb{V}\) is the small volume. Assume there are two, and only two, components of energy: kinetic energy and energy due to the compressed fluid. In going from location 1 to location 2, the pressure of this little mass of fluid changes. Change in energy due to compressing this drop of water is equal to \((\mathbb{P}_1 - \mathbb{P}_2) \Delta \mathbb{V}\). The kinetic energy also changes, and change in kinetic energy is given by
\[\frac{1}{2} m|\overrightarrow{v_{1}}|^{2}-\frac{1}{2} m|\overrightarrow{v_{2}}|^{2}=\frac{1}{2}\left(\rho_{\text {dens}} \Delta \mathbb{V}\right)\left(|\overrightarrow{v_{1}}|^{2}-|\overrightarrow{v_{2}}|^{2}\right). \nonumber \]
However, energy is conserved, so
\[\left(\mathbb{P}_{1}-\mathbb{P}_{2}\right) \Delta \mathbb{V}+\frac{1}{2}\left(\rho_{\text {dens}} \Delta \mathbb{V}\right)\left(|\overrightarrow{v_{1}}|^{2}-|\overrightarrow{v_{2}}|^{2}\right)=0. \nonumber \]
This expression can be simplified algebraically.
\[\mathbb{P}_{1}-\mathbb{P}_{2}+\frac{1}{2} \rho_{\text {dens}}\left|\vec{v}_{1}\right|^{2}-\frac{1}{2} \rho_{\text {dens}}\left|\vec{v}_{2}\right|^{2}=0 \nonumber \]
Both pressure \(\mathbb{P}\) and velocity \(\overrightarrow{v}\) are functions of location. The only way this expression can be true for all locations is if it is true for each location and a constant.
\[\mathbb{P}_{1}+\frac{1}{2} \rho_{\text {dens}}|\overrightarrow{v_{1}}|^{2}=\mathbb{P}_{2}+\frac{1}{2} \rho_{\text {dens}}|\overrightarrow{v_{2}}|^{2}=\text { constant } \nonumber \]
Bernoulli's equation with the rather severe assumptions above becomes
\[\mathbb{P}+\frac{1}{2} \rho_{\text {dens}}|\vec{v}|^{2}=\text { constant }. \label{10.5.5} \]
Bernoulli's equation is also used to describe the lift of an air foil or the path of a curve ball in baseball [162, p. 350]. In some EHDs electricity induces changes in the pressure or volume of a microfluidic channel. The fluid in these devices may be conductive or insulating. As seen by Equation \ref{10.5.5}, this change in pressure induces a change in fluid velocity.
In other EHDs, applied voltages exert forces on conductive fluids. A charged object in an external electric field \(\overrightarrow{E}\) feels a force in the direction of the electric field. A current in an external magnetic field \(\overrightarrow{B}\) feels a force. The direction of this force is perpendicular to both the direction of the current and the direction of the external magnetic field. These effects are summarized by the Lorentz force equation
\[\overrightarrow{F} = Q \left( \overrightarrow{E} +\overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]
which was discussed in Chapter 5. In that chapter, Hall effect devices and magnetohydrodynamic devices were discussed, both of which can be understood by the Lorentz force equation with an external magnetic field but no electrical field. This type of EHD can be understood by the Lorentz force equation with an external electric field but no magnetic field. The liquid in these devices must be conductive. When a voltage is applied across this type of EHD, an electric field is induced which causes the liquid to flow, and this effect is said to be due to a streaming potential [159]. A related effect called electrophoresis occurs in liquids which contain charged particles [161]. If an electric field is applied, these particles will move. This effect has been demonstrated with charged DNA molecules and charged protein molecules in solutions [161].
Other EHD devices operate by changing material polarization of an insulating liquid, and this effect is called dielectrophoresis. The concept of material polarization was discussed in Section 2.2.1. If we apply an electric field across a conductor, whether that conductor is a solid or a liquid, charges will flow. If we apply an electric field across a dielectric, the material may polarize. In other words, there will be some net charge displacement even if all electrons remain bound to atoms. The external electric field causes both the atoms of the liquid to polarize and these polarized atoms to flow.
There are a number of other interrelated EHD effects. Electroosmosis can occur in fluids with a surface charge. In some liquids, ions build up on the surface due to unpaired chemical bonds, due to ions adsorbed onto the surface, or for other reasons. If an electric field is applied across this layer of charges, the fluid will flow, and this effect is called electroosmosis [161] [159]. Also, an external electric field applied across a fluid may heat up part of the fluid and cause a temperature gradient. Fluid may flow due to the temperature gradient, and this effect is called electrothermal flow [161]. Another effect, known as electrowetting, occurs in conductive liquids. At the interface of a solid conductor and a conductive liquid, charges build up [61]. Again, if an electric field is applied, the liquid will flow.


