11.5: Capacitor Inductor Example
- Page ID
- 19008
The ideas of calculus of variations apply to energy conversion processes in electrical systems too. Consider a circuit with a capacitor and an inductor as shown in Figure \(\PageIndex{1}\). The current \(i_L\), the current \(i_c\), and the voltage \(v\) are defined in the figure. Assume that wires and components have no resistance. While this is not completely physical, it will allow us to simplify the problem. Assume that the capacitor is charged for \(t < 0\), and the switch is open. At \(t = 0\), the switch is closed, and the capacitor begins discharging. In this example, the generalized path will be the charge built up on the plates of the capacitor. We can derive the equation of motion that describes this path.
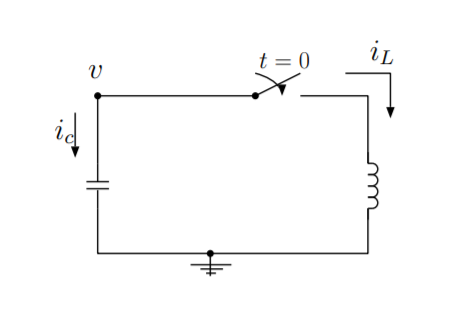
Energy is converted between two forms. The first form of energy in this system is electrical energy stored in the capacitor. The voltage \(v\) in volts across a capacitor is proportional to the charge \(Q\) in coulombs across the plates of the capacitor. Capacitance \(C\), measured in farads, is the constant of proportionality between the two measures.
\[Q = Cv \nonumber \]
The current-voltage relationship across the capacitor can be found by taking the derivative with respect to time.
\[\frac{dQ}{dt} = C\frac{dv}{dt} \label{11.5.2} \]
The change in charge build up with respect to time is the current. More specifically,
\[\frac{dQ}{dt} = i_c = -i_L. \label{11.5.3} \]
Equations \ref{11.5.2} and \ref{11.5.3} can be combined.
\[-i_L = C\frac{dv}{dt}. \nonumber \]
The energy stored in a capacitor is
\[E_{c a p}=\frac{1}{2} C v^{2}. \nonumber \]
The second form of energy in this system is the energy stored in the magnetic field of the inductor. The current \(i_L\) through the inductor, measured in amperes, is proportional to the magnetic flux \(\Psi\), measured in webers, around the inductor. Inductance \(L\), measured in henries, is the constant of proportionality between the current and magnetic flux.
\[\Psi = Li_L \nonumber \]
The current voltage relationship across this inductor can be found by taking the derivative with respect to time.
\[\frac{d \Psi}{d t}=v=L \frac{d i_{L}}{d t} \nonumber \]
The energy stored in the inductor is given by
\[E_{ind}=\frac{1}{2} L i_{L}^{2} \nonumber \]
We describe the energy conversion process by keeping track of a the generalized path \(Q(t)\), the charge stored on the capacitor. The variable \(t\) represents the independent variable time in seconds, and \(Q\) is the dependent variable charge in coulombs. The Hamiltonian and Lagrangian, \(H\) and \(L\), will be considered functions of three independent-like variables: \(t\), \(Q\), and \(\frac{dQ}{dt}\).
The Hamiltonian is the sum of the energy in the capacitor and the energy in the inductor. The Lagrangian is the difference between these energies.
\[H = E_{total} = E_{cap} + E_{ind} \nonumber \]
\[\mathcal{L} = E_{cap} - E_{ind} \nonumber \]
Electrical engineers typically describe physical circuits using the most easily measured quantities: current and voltage. However, here to illustrate the use of the calculus of variations formalism, we write expressions for both the total energy and the Lagrangian in terms of the specified variables: \(t\), \(Q\), and \(\frac{dQ}{dt}\).
\[H\left(t, Q, \frac{d Q}{d t}\right)=\frac{1}{2 C} Q^{2}+\frac{1}{2} L\left(\frac{d Q}{d t}\right)^{2} \nonumber \]
\[\mathcal{L}\left(t, Q, \frac{d Q}{d t}\right)=\frac{1}{2 C} Q^{2}-\frac{1}{2} L\left(\frac{d Q}{d t}\right)^{2} \nonumber \]
We can find the path, charge on the capacitor as a function of time, by solving for the least action
\[\delta\left|\int_{t_{1}}^{t_{2}} \mathcal{L}\left(t, x, \frac{d x}{d t}\right) d t\right|=0 \label{11.5.13} \]
or by solving the Euler-Lagrange equation,
\[\frac{\partial \mathcal{L}}{\partial Q}-\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial\left(\frac{d Q}{d t}\right)}=0. \label{11.5.14} \]
In Equation \ref{11.5.13}, \(\delta\) indicates the first variation as defined by Equation 11.3.5. Solutions depend on initial conditions such as the charge stored in the capacitor and the current in the inductor at the initial time. We can use the Euler-Lagrange equation to find the equation of motion. The first term of Equation \ref{11.5.14} is the generalized potential,
\[\frac{\partial \mathcal{L}}{\partial Q} = \frac{Q}{C} \nonumber \]
which is the voltage \(v\) in volts. The next term is the derivative of the generalized momentum.
\[\mathbb{M}=\frac{\partial \mathcal{L}}{\partial\left(\frac{d Q}{d t}\right)}=-L \frac{d Q}{d t} \nonumber \]
We can put the pieces together to find an expression of conservation of the generalized potential.
\[\frac{Q}{C}+L \frac{d^{2} Q}{d t^{2}}=0 \label{11.5.17} \]
This is a statement of Kirchhoff's voltage law. It looks more familiar if it is written in terms of voltage \(v = \frac{Q}{C}\) and current \(i_L = -\frac{dQ}{dt}\).
\[v-L \frac{d i_{L}}{d t}=0 \nonumber \]
We can solve the equation of motion, Equation \ref{11.5.17}, using appropriate initial conditions, to find the path. As in the mass spring example, Equation \ref{11.5.17} is the wave equation, and its solutions are sinusoids. As expected, a circuit made of only a capacitor and inductor is an oscillator.
| Energy storage device | Capacitor | Linear spring |
|---|---|---|
| Generalized Path | Charge \(Q\) in C | Displacement \(\overrightarrow{x}\) in m |
| Generalized Potential | Voltage \(v\) in \(\frac{J}{C} = V\) | \(\overrightarrow{F}\) Force in \(\frac{J}{m} = N\) |
| Generalized Capacity | Capacitance \(C\) in F = \(\frac{C^2}{J}\) | \(\frac{1}{K}\) in \(\frac{m^2}{J}\) |
| Constitutive relationship | \(Q=Cv\) | \(\overrightarrow{x} = \frac{1}{K}\overrightarrow{F}\) |
| Energy | \(\frac{1}{2}Cv^2\) | \(\frac{1}{2}\frac{1}{K}|\overrightarrow{x}|^2 = \frac{1}{2}K|\overrightarrow{F}|^2\) |
| Law for potential | KVL | Newton's Second Law \(\overrightarrow{F} = m\overrightarrow{a}\) |
Furthermore, we can show that energy is conserved in this energy conversion process because the partial derivative of both the total energy and the Lagrangian with respect to time are zero.
\[\frac{\partial \mathcal{L}}{\partial t}=\frac{\partial H}{\partial t}=0 \nonumber \]
\[\frac{d \mathcal{L}}{d t}=\frac{d H}{d t}=0 \nonumber \]
Table \(\PageIndex{2}\) summarizes this example. It also illustrates the relationship between parameters of this example and parameters of the mass spring example.


