3.14: Standing Wave Ratio
- Page ID
- 6280
Precise matching of transmission lines to terminations is often not practical or possible. Whenever a significant mismatch exists, a standing wave (Section 3.13) is apparent. The quality of the match is commonly expressed in terms of the standing wave ratio (SWR) of this standing wave.
Standing wave ratio (SWR) is defined as the ratio of the maximum magnitude of the standing wave to minimum magnitude of the standing wave.
In terms of the potential: \[\boxed{ \mbox{SWR} \triangleq \frac{\mbox{maximum}~|\widetilde{V}|}{\mbox{minimum}~|\widetilde{V}|} } \nonumber \]
SWR can be calculated using a simple expression, which we shall now derive. In Section 3.13, we found that:
\[\left|\widetilde{V}(z)\right| = |V_0^+| \sqrt{ 1 + \left|\Gamma\right|^2 + 2\left|\Gamma\right| \cos\left( 2\beta z + \phi \right) } \nonumber \]
The maximum value occurs when the cosine factor is equal to \(+1\), yielding: \[\mbox{max}~\left|\widetilde{V}\right| = |V_0^+| \sqrt{ 1 + \left|\Gamma\right|^2 + 2\left|\Gamma\right| } \nonumber \]
Note that the argument of the square root operator is equal to \(\left( 1 + \left|\Gamma\right| \right)^2\); therefore:
\[\mbox{max}~\left|\widetilde{V}\right| = |V_0^+| \left( 1 + \left|\Gamma\right| \right) \nonumber \]
Similarly, the minimum value is achieved when the cosine factor is equal to \(-1\), yielding:
\[\mbox{min}~\left|\widetilde{V}\right| = |V_0^+| \sqrt{ 1 + \left|\Gamma\right|^2 - 2\left|\Gamma\right| } \nonumber \]
So: \[\mbox{min}~\left|\widetilde{V}\right| = |V_0^+| \left( 1 - \left|\Gamma\right| \right) \nonumber \]
Therefore: \[\boxed{ \mbox{SWR} = \frac{1 + \left|\Gamma\right|}{1 - \left|\Gamma\right|} } \label{m0081_eSWR} \]
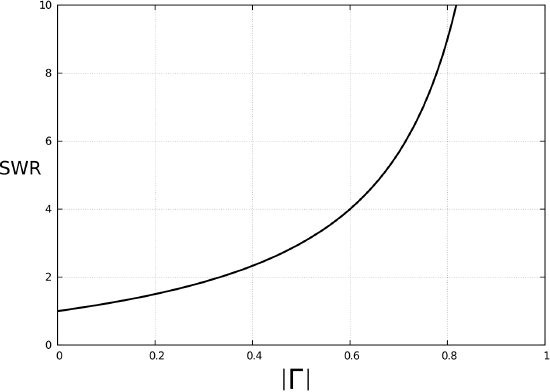
This relationship is shown graphically in Figure \(\PageIndex{1}\). Note that SWR ranges from 1 for perfectly-matched terminations (\(\Gamma=0\)) to infinity for open- and short-circuit terminations (\(\left|\Gamma\right|=1\)).
It is sometimes of interest to find the magnitude of the reflection coefficient given SWR. Solving Equation \ref{m0081_eSWR} for \(\left|\Gamma\right|\) we find: \[\left|\Gamma\right| = \frac{\mbox{SWR}-1}{\mbox{SWR}+1} \label{m0081_eGammaFromSWR} \]
SWR is often referred to as the voltage standing wave ratio (VSWR), although repeating the analysis above for the current reveals that the current SWR is equal to potential SWR, so the term “SWR” suffices.
SWR \(<2\) or so is usually considered a “good match,” although some applications require SWR \(<1.1\) or better, and other applications are tolerant to SWR of 3 or greater.
What is the reflection coefficient for the above-cited values of SWR? Using Equation \ref{m0081_eGammaFromSWR}, we find:
- SWR = 1.1 corresponds to \(\left|\Gamma\right|=0.0476\).
- SWR = 2.0 corresponds to \(\left|\Gamma\right|=1/3\).
- SWR = 3.0 corresponds to \(\left|\Gamma\right|=1/2\).


