9.4: Measures of Batteries and Fuel Cells
- Page ID
- 18994
Cell Voltage, Specific Energy, and Related Measures
Just as chemists have multiple measures of the ability of charges to flow, they have multiple measures of energy or charge stored in a device. In this section, the following measures of batteries and fuel cells are defined:
- Cell voltage in volts
- Specific energy in \(\frac{J}{g}\) or \(\frac{W \cdot h}{kg}\)
- Energy density in \(\frac{J}{m^3}\) or \(\frac{W \cdot h}{L}\)
- Capacity in \(mA \cdot h\) or \(C\)
- Specific capacity in \(\frac{mA \cdot h}{g}\) or \(\frac{C}{kg}\)
- Charge density in \(\frac{mA \cdot h}{L}\) or \(\frac{C}{L}\)
Definitions throughout this section follow references [128, ch. 1] and [140].
If these measures are calculated using knowledge of chemical reactions and quantities found in the periodic table, they are called theoretical values. If these quantities are experimentally measured, they are called practical values. Practical values are necessarily less because no energy conversion device is ever completely efficient. Measures preceded by the word specific are given per unit mass. Measures followed by the word density are give per unit volume. For example, specific energy is measured in the SI units of joules per gram and energy density is measured in the SI units of joules per meter cubed. However, these rules are not closely followed, so the term energy density is sometimes used to mean energy per unit weight instead of per unit volume. It is safest to explicitly specify the units of measure to avoid this confusion.
Theoretical cell voltage, \(V_{cell}\) measured in volts, is the voltage between the anode and the cathode in a battery or fuel cell. It is the sum of the redox potential for the half reaction at the anode and the redox potential for the half reaction at the cathode. It represents the voltage between the terminals of a completely charged battery or fuel cell. Many authors call this measure theoretical cell potential instead of cell voltage, and symbols \(E^0\) or \(\Xi^0\) are also used in the literature. As discussed in Appendix C, the word potential is overloaded with multiple meanings. The word voltage and the symbol \(V_{cell}\) are used here to emphasize that this quantity is essentially voltage. Since redox potentials for many half reactions are tabulated [128, app. B] [137], theoretical cell voltage can be quickly calculated for many reactions. While we can calculate the theoretical cell voltage, we can measure the practical cell voltage with a voltmeter. The theoretical cell voltage will always be slightly larger than the practical cell voltage because the theoretical cell voltage ignores a number of effects including internal resistance and other factors discussed in the next section. Reactions with \(V_{cell} > 0\) occur spontaneously [12, ch. 18].
Three related measures are capacity, specific capacity, and charge density. Capacity is measured in ampere hours or coulombs. (By definition, one ampere is equal to one coulomb per second.) It is a measure of the charge stored in a battery or fuel cell. Specific capacity is a measure of the charge stored per unit mass. It is specified in \(\frac{mA \cdot h}{g}\), \(\frac{C}{kg}\), or related units. Charge density is a measure of the charge stored per unit volume, and it is specified in \(\frac{mA \cdot h}{L}\), \(\frac{C}{m^3}\), or related units. While capacity depends on the amount of material present, specific capacity and charge density do not. All of these measures may be specified as theoretical values calculated from knowledge of the chemical reactions involved or practical values measured experimentally where the theoretical values are always slightly higher. Also for all of these values, only valence electrons are considered. Batteries and fuel cells necessarily have more electrons than are included in these measures because inner shell electrons, which do not participate in the chemical reaction, are ignored. Energy is stored in the bonds holding inner shell electrons, but this energy is not converted to electricity in batteries or fuel cells. The concept of charge density, \(\rho_{ch}\) in units \(\frac{C}{m^3}\), was first introduced in section 1.6.1, and it shows up in Gauss's law, one of Maxwell's equations. However, the word capacity has nothing to do with the word capacitance introduced earlier. See Appendix C for more information on this and other overloaded terms.
Theoretical specific energy is measured in \(\frac{J}{g}\), \(\frac{W \cdot h}{kg}\), or related units [128, ch. 1]. It is a measure of the energy stored in a battery or fuel cell per unit weight. It is the product of the theoretical cell voltage and the specific charge. Relatedly, theoretical energy density, measured in \(\frac{J}{m^3}\) or \(\frac{W \cdot h}{L}\), is a measure of the energy stored in a device per unit volume. Theoretical energy density is the product of theoretical cell voltage and charge density. These measures can be calculated from knowledge of the chemical reactions involved using information found in the periodic table. Practical specific energy and practical energy density are typically 25-35% below the theoretical values [128, ch. 1.5]. Specific energy and energy density are important measures of a battery. Often, high values are desired so that small and light batteries can be used to power devices for as long as possible. However, as specific energy and energy density increase, safety considerations increase.
Chemists sometimes define the charge in a mol of electrons as the Faraday constant. It has the value
\[\frac{6.022 \cdot 10^{23} \text { atoms }}{1 \mathrm{mol}} \cdot \frac{1 e^{-}}{\operatorname{atom}} \cdot \frac{1.602 \cdot 10^{-19} \mathrm{C}}{e^{-}}=9.649 \cdot 10^{4} \frac{\mathrm{C}}{\mathrm{mol}} \nonumber \]
[68]. This quantity will not be used below because the Avogadro constant \(N_a\) and the magnitude of the charge of an electron \(q\) are already specified and because this text already has too many variables.
We can calculate the theoretical specific capacity in \(\frac{A \cdot h}{g}\) and the theoretical specific energy in \(\frac{J}{g}\) for the reactions given by Equation 9.3.1 and 9.3.2. The redox potential for the Mg half reaction is \(V_{rp} = 2.68\) V, and the redox potential for the Ni half reaction is \(V_{rp} = 0.49\) V [140] [137]. The overall cell voltage is
\[V_{cell} = 2.68 + 0.49 = 3.17 \text{V}. \nonumber \]
The reaction occurs spontaneously when it is set up because \(V_{cell} > 0\).
By unit conversions, we can calculate the weight per unit charge for each half reaction. From the periodic table, the atomic weight of Mg is 24.31 \(\frac{g}{mol}\), the atomic weight of Ni is 58.69 \(\frac{g}{mol}\), and the atomic weight of O is 16.00 \(\frac{g}{mol}\). First consider the Mg half reaction of Equation 9.3.1 which involves two valence electrons.
\[24.31 \frac{\mathrm{g}}{\mathrm{mol}} \cdot \frac{1 \mathrm{mol}}{6.022 \cdot 10^{23} \mathrm{atoms}} \cdot \frac{1 \text { atom }}{2 \text { valence } e^{-}} \cdot \frac{1 e^{-}}{1.602 \cdot 10^{-19} \mathrm{C}} \cdot \frac{1 \mathrm{C}}{1 \mathrm{A} \cdot \mathrm{s}} \cdot \frac{3600 \mathrm{s}}{1 \mathrm{h}} = 0.454 \frac{\mathrm{g}}{\mathrm{A} \cdot \mathrm{h}} \nonumber \]
Next, consider the Ni half reaction of Equation 9.3.2 which also involves two valence electrons. The weight of NiO\(_2\) is 90.69 \(\frac{g}{mol}\).
\[90.69 \frac{\mathrm{g}}{\mathrm{mol}} \cdot \frac{1 \mathrm{mol}}{6.022 \cdot 10^{23} \mathrm{atoms}} \cdot \frac{1 \text { atom }}{2 \text { valence } e^{-}} \cdot \frac{1 e^{-}}{1.602 \cdot 10^{-19} \mathrm{C}} \cdot \frac{1 \mathrm{C}}{1 \mathrm{A} \cdot \mathrm{s}} \cdot \frac{3600 \mathrm{s}}{1 \mathrm{h}} = 1.69 \frac{\mathrm{g}}{\mathrm{A} \cdot \mathrm{h}} \nonumber \]
For the overall reaction,
\[0.454+1.692=2.146 \frac{\mathrm{g}}{\mathrm{A} \cdot \mathrm{h}}. \nonumber \]
The overall theoretical specific capacity is the inverse of this quantity.
\[\frac{1}{2.146} = 0.466\frac{\mathrm{A} \cdot \mathrm{h}}{\mathrm{g}} \nonumber \]
Adding charge densities for each half reaction does not make sense, but we can sum the terms for weight per unit charge in unit \(\frac{g}{A \cdot h}\).
We can calculate the theoretical specific energy by multiplying the theoretical cell voltage and the theoretical specific capacity.
\[3.17 \mathrm{V} \cdot 0.466 \frac{\mathrm{A} \cdot \mathrm{h}}{\mathrm{g}}=1.48 \frac{\mathrm{W} \cdot \mathrm{h}}{\mathrm{g}} \nonumber \]
The theoretical specific energy can be converted to the units \(\frac{J}{g}\).
\[1.48 \frac{\mathrm{W} \cdot \mathrm{h}}{\mathrm{g}} \cdot \frac{1 \mathrm{J}}{1 \mathrm{W} \cdot \mathrm{s}} \cdot \frac{3600 \mathrm{s}}{1 \mathrm{h}}=5.32 \cdot 10^{3} \frac{\mathrm{J}}{\mathrm{g}} \nonumber \]
In the calculation above, only the electrode weights were considered. However, the package, separator, and other battery components all have some mass which contribute to the weight of the battery.
Practical Voltage and Efficiency
We can model both a battery and a fuel cell as an ideal voltage source. This is a useful model, but at times, it is not good enough for multiple reasons. A better model includes some internal resistance [128, p. 9.27]. However, even this model is inadequate because the voltage of any practical battery depends on temperature, the load, the current through the battery, the fraction of capacity used, the number of times it has been recharged, and other factors [128, p. 3.2]. An even better model includes these variations too, as shown in Fig. \(\PageIndex{1}\).
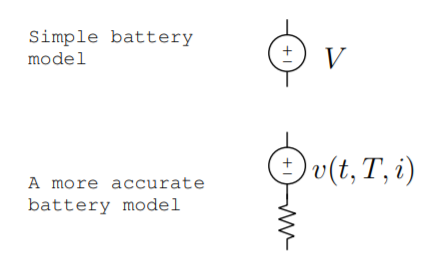
There are many measures used to describe the voltage across a battery or fuel cell. The nominal voltage is the typical voltage during use, and it is often the voltage printed on the label. The end or cutoff voltage is the voltage at the end of the battery's useful life. The open circuit voltage is the voltage under no load, and it is approximately the initial voltage of the battery. The closed circuit voltage is the voltage under load. It is less than the open circuit voltage due to the internal resistance of the battery [128, p. 3.2].
All batteries and fuel cells have some internal resistance. The cathode and anode are made of metals which are good, but imperfect, conductors. For example, carbon is a common electrode material, and it has an electrical conductivity between \(1.6 \cdot 10^4\) and \(2.0 \cdot 10^7 \frac{1}{\Omega \cdot m}\) [106]. Anytime current flows through a physical material with finite electrical conductivity, energy is converted to heat. Actual voltage is a function of current drawn from the battery because at high currents, this effect is larger. Also, the actual voltage is a function of temperature because ions move faster at higher temperatures, so there is less internal resistance at higher temperatures [128, p. 3.9]. However, at higher temperatures, chemical reactions may occur more quickly, so the life of the batteries may be less because reactions occur faster.
The actual voltage across a battery or fuel cell is also influenced by the accumulation of chemical reaction products. In the example given by Equations Equation 9.3.1 and 9.3.2, the reactants were Mg and NiO\(_2\) and the reaction products were Mg(OH)\(_2\) and Ni(OH)\(_2\). The actual voltage across the device decays with use because reactants build up in the electrolyte as the reaction occurs. These reactants inhibit further reactions from taking place [128, p. 3.2]. The effect of the accumulation of products on the voltage of a battery can be modeled by
\[V_{cell\,theor}-V_{cell\,prac} = \frac{k_{B} T}{N_{v} q} \ln \left(\frac{[\text { products }]}{[\text { reactants }]}\right) \nonumber \]
which is known as the Nernst equation [12, p. 750,789]. Many authors replace the Boltzmann constant in this expression using \(\mathbb{R} = N_ak_B\) where \(N_a\) is the Avogadro constant and \(\mathbb{R}\) is the molar gas constant. In this expression, \(V_{cell\,theor}\) is the theoretical cell voltage, and \(V_{cell\,prac}\) is the practical cell voltage that incorporates the effect of reaction products. The quantity \(N_v\) represents the number of valence electrons involved in the chemical reaction. For the example of Equation 9.3.1 and 9.3.2, two electrons are involved. So, the quantity \(\frac{k_BT} {N_v}\) represents the internal energy per valence electron involved in the reaction. The quantity \(\frac{[\text { products }]}{[\text { reactants }]}\) is known as the activity quotient, and its natural log is between zero and one.
\[0 \leq \ln \left(\frac{[\text { products }]}{[\text { reactants }]}\right) \leq 1 \nonumber \]
When a battery is first set up, there are many reactants but few products present, and
\[\ln \left(\frac{[\text { products }]}{[\text { reactants }]}\right) \approx 0. \nonumber \]
In this case, the activity quotient is very small, so the practical cell voltage between the terminals is very close to the theoretical cell voltage. After a battery has been discharging for a long time, the activity quotient is large because many products are present.
\[\ln \left(\frac{[\text { products }]}{[\text { reactants }]}\right) \approx 1 \nonumber \]
As expected, this model shows that as a battery discharges, the difference between the theoretical and practical cell voltage grows. We cannot ever use the entire capacity stored in a battery. As the battery discharges, the voltage between the terminals drops. At some point, the voltage level is too low to be useful, and the end voltage is reached. At this point, the battery should be replaced even though it still has some stored charge.
The Nernst equation is useful to chemists because it can be used to solve for the amount concentration of reaction products and reactants. The theoretical cell voltage can be calculated or found in a table, and the practical cell voltage can be measured with a voltmeter. Reference [137] tabulates components of the activity quotient as a function of temperature for various reactions.
Electrical engineers may be more interested in the Nernst equation because it gives information on the efficiency of batteries and fuel cells. Efficiency is defined as the output power over the input power or the output energy over the input energy.
\[\eta_{ef\,f} = \frac{E_{out}}{E_{in}} \nonumber \]
Energy stored in an electrical component is given by Equation 2.2.7 where Q is charge and V is voltage. The amount of charge involved in each reaction is given by number of electrons involved times their charge for each, \(Q = qN_v\).
\[E_{in} = \frac{1}{2}qN_vV_{cell\,theor} \label{9.4.14} \]
Internal energy of a reaction at temperature \(T\) is also given by
\[E_{in} = \frac{1}{2}k_BT \label{9.4.15} \]
We can model the theoretical voltage of a battery cell by combining Equations \ref{9.4.14} and \ref{9.4.15}.
\[k_BT = qN_vV_{cell\,theor} \nonumber \]
\[V_{cell\,theor} = \frac{k_BT}{qN_v} \nonumber \]
The output energy produced by the battery is proportional to the practical cell voltage measured between the terminals.
\[E_{out} = \frac{1}{2}qN_vV_{cell\,prac} \nonumber \]
The efficiency can then be rewritten.
\[\eta_{ef\,f} = \frac{V_{cell\,prac}}{V_{cell\,theor}} \nonumber \]
With some algebra, we can use the Nernst equation to write this quantity as a function of the activity quotient.
\[\eta_{ef\,f} = \frac{V_{cell\,prac}+V_{cell\,theor}-V_{cell\,theor}}{V_{cell\,theor}} \nonumber \]
\[\eta_{ef\,f} = 1-\left( \frac{V_{cell\,theor}-V_{cell\,prac}}{V_{cell\,te}}\right) \nonumber \]
The numerator can be replaced using the Nernst equation.
\[\eta_{ef\,f} =1- \frac{1}{V_{cell\,theor}} \left( \frac{k_BT}{N_vq} \ln \left(\frac{[\text { products }]}{[\text { reactants }]}\right) \right) \nonumber \]
\[\eta_{ef\,f} =1- \ln \left(\frac{[\text { products }]}{[\text { reactants }]}\right) \label{9.4.23} \]
Equation \ref{9.4.23} shows that the efficiency is a function of the activity quotient. As described above, the activity quotient is different for different reactions, and it varies with temperature. The activity quotient is a measure of the effect of the accumulation of products in the electrolyte of a battery or fuel cell.
Equation \ref{9.4.23} describes the efficiency of batteries and fuel cells. It is another way of expressing the Nernst equation. It is analogous to equations we have encountered describing efficiency of other energy conversion devices. More specifically, it has a similar form to the equation for the Carnot efficiency, Equation 8.6.6. Carnot efficiency describes the temperature dependence of the efficiency of all devices which convert a temperature difference to another form of energy. It was introduced in the context of thermoelectric devices, but it applies to pyroelectric devices, steam turbines, and other devices too. These equations also have a similar form to Equation 7.3.4 which modeled the effect of mirror reflectivity and optical absorption on the efficiency of a laser.


