Skip to main content
Engineering LibreTexts

6.6: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    25277

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Analysis

    (All source values are in amps or volts unless specified otherwise)

    1. Given the circuit in Figure \(\PageIndex{1}\), use nodal analysis to determine \(v_c\). \(I_1 = 3\angle 0^{\circ}\), \(I_2 = 0.9\angle 0^{\circ}\).

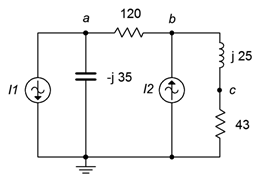
    clipboard_ec58adcb8d61eb226b03d3b2baaf05950.png

    Figure \(\PageIndex{1}\)

    2. Use nodal analysis to find the current through the 120 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{2}\). \(I_1 = 0.5\angle 90^{\circ}\), \(I_2 = 1.6\angle 0^{\circ}\).

    3. Use nodal analysis to find the current through the 43 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{2}\). The sources are in phase.

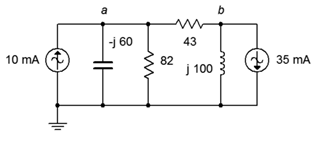
    clipboard_e7eb48029c9d6827a5b44602c3b072385.png

    Figure \(\PageIndex{2}\)

    4. Given the circuit in Figure \(\PageIndex{2}\), use nodal analysis to determine \(v_b\). The sources are in phase.

    5. Given the circuit in Figure \(\PageIndex{3}\), determine \(v_c\). \(I_1 = 3\angle 0^{\circ}\), \(I_2 = 2\angle 0^{\circ}\).

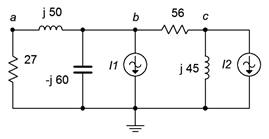
    clipboard_ef85e1fa9b47f426c59a11c68cbfce4fc.png

    Figure \(\PageIndex{3}\)

    6. Use nodal analysis to find the current through the \(j45 \Omega\) inductor in the circuit of Figure \(\PageIndex{3}\). \(I_1 = 2\angle 0^{\circ}\), \(I_2 = 1.5\angle 60^{\circ}\).

    7. Use nodal analysis to find the current through the 4 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{4}\). \(I_1 = 1\angle 45^{\circ}\), \(I_2 = 2\angle 45^{\circ}\).

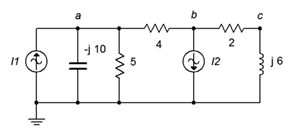
    clipboard_efcd4b0af131a136013630bc1e437fa02.png

    Figure \(\PageIndex{4}\)

    8. Given the circuit in Figure \(\PageIndex{4}\), use nodal analysis to determine \(v_c\). \(I_1 = 6\angle 30^{\circ}\), \(I_2 = 4\angle 0^{\circ}\).

    9. Given the circuit in Figure \(\PageIndex{5}\), use nodal analysis to determine \(v_{ac}\). \(I_1 = 10\angle 0^{\circ}\), \(I_2 = 6\angle 0^{\circ}\).

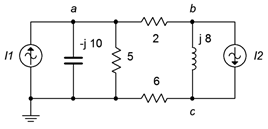
    clipboard_e944593e1aa17154bc3fe49ff81d26646.png

    Figure \(\PageIndex{5}\)

    10. Use nodal analysis to find the current through the \(j8 \Omega\) inductor in the circuit of Figure \(\PageIndex{5}\). \(I_1 = 3\angle 0^{\circ}\), \(I2 = 5\angle 30^{\circ}\).

    11. Use nodal analysis to find the current through the 22 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{6}\). \(I_1 = 800E−3\angle 0^{\circ}\), \(I_2 = 2.5\angle 0^{\circ}\), \(I_3 = 2\angle 20^{\circ}\).

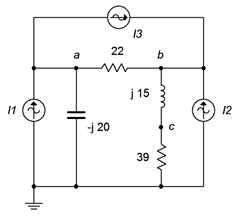
    clipboard_e9ba503513f8244ca2f4181c5d3a2522f.png

    Figure \(\PageIndex{6}\)

    12. Given the circuit in Figure \(\PageIndex{6}\), use nodal analysis to determine \(v_c\). \(I_1 = 4\angle 90^{\circ}\), \(I_2 = 10\angle 120^{\circ}\), \(I_3 = 5\angle 0^{\circ}\).

    13. Given the circuit in Figure \(\PageIndex{7}\), use nodal analysis to determine \(v_c\). \(I_1 = 3E−3\angle 0^{\circ}\), \(I_2 = 10E−3\angle 0^{\circ}\), \(I_3 = 2E−3\angle 0^{\circ}\).

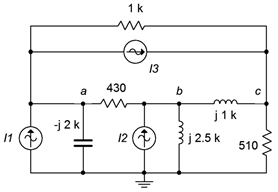
    clipboard_e2f6ad9a6ebc672f39316540967a88f84.png

    Figure \(\PageIndex{7}\)

    14. Use nodal analysis to find the current through the \(−j2\) k\(\Omega\) capacitor in the circuit of Figure \(\PageIndex{7}\). \(I_1 = 1E−3\angle 0^{\circ}\), \(I_2 = 5E−3\angle 0^{\circ}\), \(I_3 = 6E−3\angle −90^{\circ}\).

    15. Use nodal analysis to find the current through the 3.3 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{8}\). \(E = 36\angle 0^{\circ}\), \(I = 4E−3\angle −120^{\circ}\).

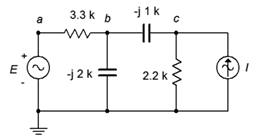
    clipboard_ebe1aba21d7916092d75e448794a89f61.png

    Figure \(\PageIndex{8}\)

    16. Given the circuit in Figure \(\PageIndex{8}\), write the node equations and determine \(v_c\). \(E = 18\angle 0^{\circ}\), \(I = 7.5E−3\angle −30^{\circ}\).

    17. Given the circuit in Figure \(\PageIndex{9}\), use nodal analysis to determine \(v_c\). \(E = 40\angle 180^{\circ}\), \(I = 20E−3\angle 0^{\circ}\).

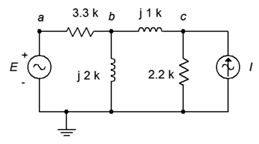
    clipboard_ebde83a8bd0a22c15001dd7a14dbfee39.png

    Figure \(\PageIndex{9}\)

    18. Use nodal analysis to find the current through the 2.2 k\(\Omega\) resistor in Figure \(\PageIndex{9}\). \(E = 240\angle 0^{\circ}\), \(I = 100E−3\angle 0^{\circ}\).

    19. Use nodal analysis to find \(v_{bc}\) in the circuit of Figure \(\PageIndex{10}\).

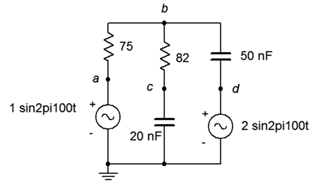
    clipboard_ed9b76a9659e52c7076f472f49de3c46d.png

    Figure \(\PageIndex{10}\)

    20. Use nodal analysis to find the current through the 2.7 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{11}\).

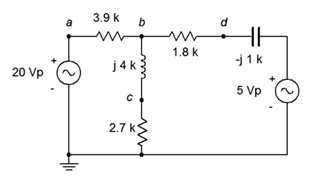
    clipboard_e7b6fe3234c821e373cf5dd02e8ef0bb0.png

    Figure \(\PageIndex{11}\)

    21. Given the circuit in Figure \(\PageIndex{12}\), use nodal analysis to determine \(v_{ba}\). \(E_1 = 1\angle 0^{\circ}\), \(E_2 = 2\angle 0^{\circ}\).

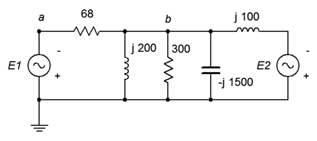
    clipboard_e63983b6dc23c15ad102116fb0f179993.png

    Figure \(\PageIndex{12}\)

    22. Given the circuit in Figure \(\PageIndex{13}\), use nodal analysis to determine \(v_{ad}\). \(E_1 = 9\angle 0^{\circ}\), \(E_2 = 5\angle 40^{\circ}\).

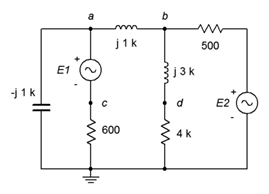
    clipboard_e42f1741f4b29aca8b4a3dd6f268424a2.png

    Figure \(\PageIndex{13}\)

    23. Use nodal analysis to find \(v_{cb}\) in the circuit of Figure \(\PageIndex{14}\). \(E_1 = 10\angle −180^{\circ}\), \(E_2 = 25\angle 0^{\circ}\).

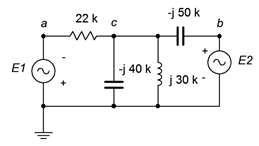
    clipboard_e00c9713884c72f701d18db6ad27a6c78.png

    Figure \(\PageIndex{14}\)

    24. Given the circuit in Figure \(\PageIndex{15}\), use nodal analysis to determine \(v_{bc}\). \(E = 20\angle 0^{\circ}\), \(R_1\) = 10 k\(\Omega\), \(R_2\) = 30 k\(\Omega\), \(R_3\) = 1 k\(\Omega\), \(X_C = −j15\) k\(\Omega\), \(X_L = j20\) k\(\Omega\).

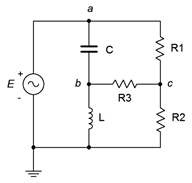
    clipboard_ebf5789ad3de2a480f31a62a3b3361da4.png

    Figure \(\PageIndex{15}\)

    25. Given the circuit in Figure \(\PageIndex{16}\), write the mesh loop equations and determine \(v_b\).

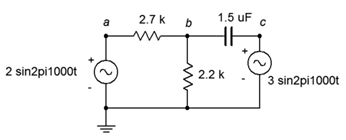
    clipboard_eede5bb788be2d10bf98fb22ad6bd990b.png

    Figure \(\PageIndex{16}\)

    26. Use mesh analysis to find the current through the 2.7 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{16}\).

    27. Use mesh analysis to find the current through the 75 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{10}\).

    28. Given the circuit in Figure \(\PageIndex{10}\), write the mesh loop equations and determine \(v_c\).

    29. Given the circuit in Figure \(\PageIndex{11}\), write the mesh loop equations and determine \(v_b\).

    30. Use mesh analysis to find the current through the 1.8 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{11}\).

    31. Use mesh analysis to find the current through the \(j200 \Omega\) inductor in Figure \(\PageIndex{12}\). \(E_1 = 1\angle 0^{\circ}\), \(E_2 = 2\angle 0^{\circ}\).

    32. Given the circuit in Figure \(\PageIndex{12}\), write the mesh loop equations and determine \(v_b\). Consider using parallel simplification first. \(E_1 = 36\angle −90^{\circ}\), \(E_2 = 24\angle −90^{\circ}\).

    33. Given the circuit in Figure \(\PageIndex{13}\), use mesh analysis to determine \(v_{cd}\). \(E_1 = 0.1\angle 0^{\circ}\), \(E_2 = 0.5\angle 0^{\circ}\).

    34. Use mesh analysis to find the current through the 600 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{13}\). \(E_1 = 9\angle 0^{\circ}\), \(E_2 = 5\angle 40^{\circ}\).

    35. Use mesh analysis to find the current through the \(−j200 \Omega\) capacitor in the circuit of Figure \(\PageIndex{17}\). \(E_1 = 18\angle 0^{\circ}\), \(E_2 = 12\angle 90^{\circ}\).

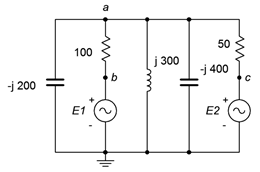
    clipboard_ede0b227c220a31b08f65c8bfee2df0bb.png

    Figure \(\PageIndex{17}\)

    36. Given the circuit in Figure \(\PageIndex{17}\), use mesh analysis to determine \(v_{ac}\). \(E_1 = 1\angle 0^{\circ}\), \(E_2 = 500E−3\angle 0^{\circ}\).

    37. Given the circuit in Figure \(\PageIndex{14}\), use mesh analysis to determine \(v_c\). \(E_1 = 10\angle −180^{\circ}\), \(E_2 = 25\angle 0^{\circ}\).

    38. Use mesh analysis to find the current through the 22 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{14}\). \(E_1 = 24\angle 0^{\circ}\), \(E_2 = 36\angle 0^{\circ}\).

    39. Use mesh analysis to find the current through the \(j300 \Omega\) inductor in Figure \(\PageIndex{18}\). \(E_1 = 1\angle 0^{\circ}\), \(E_2 = 10\angle 90^{\circ}\).

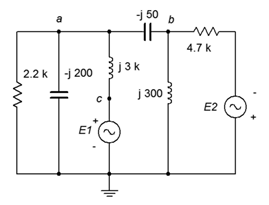
    clipboard_e1df374c0f1f0616bab6a7610cd6a0c39.png

    Figure \(\PageIndex{18}\)

    40. Given the circuit in Figure \(\PageIndex{18}\), use mesh analysis to determine \(v_a\). \(E_1 = 100\angle 0^{\circ}\), \(E_2 = 90\angle 0^{\circ}\).

    41. Given the circuit in Figure \(\PageIndex{15}\), use mesh analysis to determine \(v_{bc}\). \(E = 10\angle 0^{\circ}\), \(R_1\) = 1 k\(\Omega\), \(R_2\) = 2 k\(\Omega\), \(R_3\) = 3 k\(\Omega\), \(X_C = −j4\) k\(\Omega\), \(X_L = j8\) k\(\Omega\).

    42. Use mesh analysis to find the current through resistor \(R_3\) in the circuit of Figure \(\PageIndex{15}\). \(E = 20\angle 0^{\circ}\), \(R_1\) = 10 k\(\Omega\), \(R_2\) = 30 k\(\Omega\), \(R_3\) = 1 k\(\Omega\), \(X_C = −j15\) k\(\Omega\), \(X_L = j20\) k\(\Omega\).

    43. Use mesh analysis to find the current through resistor \(R_3\) in Figure \(\PageIndex{19}\). \(E = 60\angle 0^{\circ}\), \(R_1\) = 1 k\(\Omega\), \(R_2\) = 2 k\(\Omega\), \(R_3\) = 3 k\(\Omega\), \(X_C = −j10\) k\(\Omega\), \(X_L = j20\) k\(\Omega\).

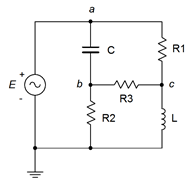
    clipboard_ecb8a706639ea816022d34b95e03afdd0.png

    Figure \(\PageIndex{19}\)

    44. Given the circuit in Figure \(\PageIndex{19}\), use mesh analysis to determine \(v_{bc}\). \(E = 120\angle 90^{\circ}\), \(R_1\) = 100 k\(\Omega\), \(R_2\) = 20 k\(\Omega\), \(R_3\) = 10 k\(\Omega\), \(X_C = −j5\) k\(\Omega\), \(X_L = j20\) k\(\Omega\).

    45. Given the circuit in Figure \(\PageIndex{20}\), use mesh analysis to determine \(v_b\). Consider using source conversion. \(E = 12\angle 0^{\circ}\), \(I = 10E−3\angle 0^{\circ}\).

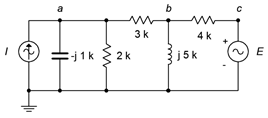
    clipboard_ed73d24c02d0d83d680356f3493b24462.png

    Figure \(\PageIndex{20}\)

    46. Use mesh analysis to find the current through the 3 \(\Omega\) resistor in the circuit in Figure \(\PageIndex{20}\). Consider using source conversion. \(E = 15\angle 90^{\circ}\), \(I = 10E−3\angle 0^{\circ}\).

    47. Use mesh analysis to find the current through the 2.2 k\(\Omega\) resistor in the circuit in Figure \(\PageIndex{21}\). \(E = 3.3\angle 0^{\circ}\), \(I = 2.1E−3\angle 0^{\circ}\).

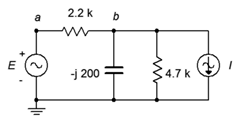
    clipboard_e53b91b9cb43140eb4db12df6ba742d7b.png

    Figure \(\PageIndex{21}\)

    48. Given the circuit in Figure \(\PageIndex{21}\), use mesh analysis to determine \(v_b\). \(E = 10\angle 0^{\circ}\), \(I = 30E−3\angle 90^{\circ}\).

    49. Given the circuit in Figure \(\PageIndex{22}\), use nodal analysis to determine \(v_{ab}\).

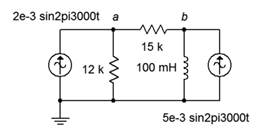
    clipboard_eb05bf6a38837fa4e15edcff0e6feec8e.png

    Figure \(\PageIndex{22}\)

    50. Use nodal analysis to find the current through the 100 mH inductor in the circuit of Figure \(\PageIndex{22}\).

    51. Use nodal analysis to find the current through the 330 \(\Omega\) resistor in the circuit of Figure \(\PageIndex{23}\).

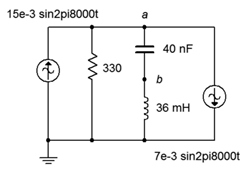
    clipboard_e07a977d9861ca61fd227a0e91d54c2be.png

    Figure \(\PageIndex{23}\)

    52. Given the circuit in Figure \(\PageIndex{23}\), write the node equations and determine \(v_b\).

    53. Given the circuit in Figure \(\PageIndex{19}\), use nodal analysis to determine \(v_{bc}\). \(E = 120\angle 0^{\circ}\), \(R_1\) = 1 k\(\Omega\), \(R_2\) = 2 k\(\Omega\), \(R_3\) = 3 k\(\Omega\), \(X_C = −j10\) k\(\Omega\), \(X_L = j20\) k\(\Omega\).

    54. Determine the current through the 10 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{24}\) if \(I_1 = 10E−3\angle −90^{\circ}\).

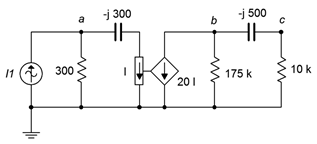
    clipboard_ed8f349c60101c27f5e9d691f531ead15.png

    Figure \(\PageIndex{24}\)

    55. Determine \(v_b\) in the circuit of Figure \(\PageIndex{24}\) if the source \(I_1 = 20E−3\angle 0^{\circ}\).

    56. Determine \(v_c\) in the circuit of Figure \(\PageIndex{25}\) if the source \(E = 3\angle 120^{\circ}\).

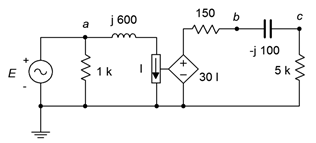
    clipboard_e1218ac11dad910dd86bb849c15b48b40.png

    Figure \(\PageIndex{25}\)

    57. Determine the current through the 5 k\(\Omega\) resistor in the circuit of Figure \(\PageIndex{25}\) if \(E = 10\angle 0^{\circ}\).

    58. In the circuit of Figure \(\PageIndex{26}\), determine the capacitor current if the source \(E = 12\angle 0^{\circ}\).

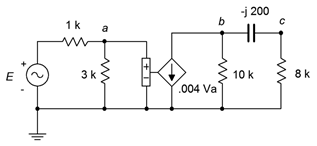
    clipboard_e101f48b5b4a39d77c02454a122dc7343.png

    Figure \(\PageIndex{26}\)

    59. In the circuit of Figure \(\PageIndex{26}\), determine \(v_c\) if the source \(E = 8\angle 90^{\circ}\).

    60. In the circuit of Figure \(\PageIndex{27}\), determine \(v_b\) if the source \(E = 12\angle −90^{\circ}\).

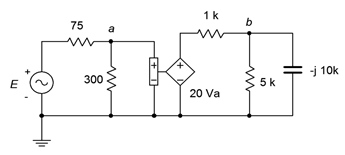
    clipboard_e5ea000d27ada7d0d2d6fee64a9ea7773.png

    Figure \(\PageIndex{27}\)

    61. In the circuit of Figure \(\PageIndex{27}\), determine the current flowing into the 1 k\(\Omega\) resistor if the source \(E = 6\angle 0^{\circ}\).

    62. In the circuit of Figure \(\PageIndex{28}\), determine the current flowing into the 600 \(\Omega\) resistor if \(I_1 = 1E−3\angle 180^{\circ}\).

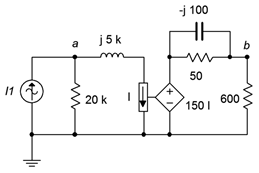
    clipboard_e50bdf75761d7974c76fded54bdf42ed1.png

    Figure \(\PageIndex{28}\)

    63. Determine \(v_a\) and \(v_b\) in the circuit of Figure \(\PageIndex{28}\) if the source \(I_1 = 2E−3\angle 0^{\circ}\).

    64. Determine \(v_a\) in the circuit of Figure \(\PageIndex{29}\) if the source \(E = 2\angle 0^{\circ}\).

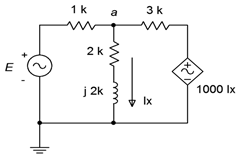
    clipboard_e6404cb18b572a95c382d0f34cdd82b7e.png

    Figure \(\PageIndex{29}\)

    65. Given the circuit in Figure \(\PageIndex{29}\), determine the current flowing through the 1 k\(\Omega\) resistor. Assume that \(E = 15\angle 45^{\circ}\).

    66. Given the circuit in Figure \(\PageIndex{30}\), determine the current flowing through the 3 k\(\Omega\) resistor if the source \(E = 25\angle 33^{\circ}\).

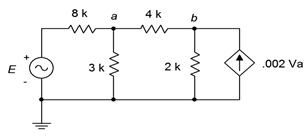
    clipboard_e5cae3f29b3373dfdf6aae0b6bf06f864.png

    Figure \(\PageIndex{30}\)

    67. Given the circuit in Figure \(\PageIndex{30}\), determine \(v_{ab}\). Assume the source \(E = 15\angle −112^{\circ}\).

    68. In the circuit of Figure \(\PageIndex{31}\), determine \(v_d\).

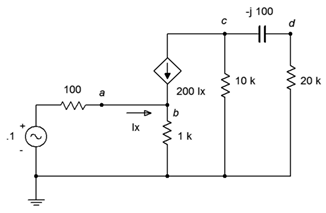
    clipboard_ee43b1ef013a7651bddf8afad7796d0d8.png

    Figure \(\PageIndex{31}\)

    69. Given the circuit in Figure \(\PageIndex{31}\), determine the current flowing through the 1 k\(\Omega\) resistor.

    70. Given the circuit in Figure \(\PageIndex{32}\), determine the current flowing through the 100 \(\Omega\) resistor.

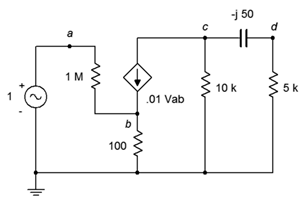
    clipboard_e08063c7c1a43492f7a8ae35310fcd7c7.png

    Figure \(\PageIndex{32}\)

    71. Determine \(v_d\) in the circuit of Figure \(\PageIndex{32}\).

    72. Determine \(v_{ab}\) in the circuit of Figure \(\PageIndex{33}\). \(E = 10\angle 0^{\circ}\)

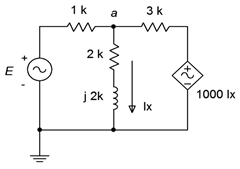
    clipboard_e22e0966f657782f27a68be430be7d281.png

    Figure \(\PageIndex{33}\)

    Challenge

    73. Given the circuit in Figure \(\PageIndex{34}\), write the node equations. \(E_1 = 50\angle 0^{\circ}\), \(E_2 = 35\angle 120^{\circ}\), \(I = 500E−3\angle 90^{\circ}\).

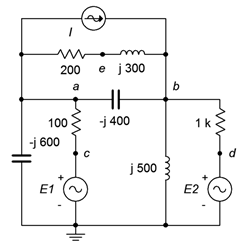
    clipboard_ed21f2a28126f5e109553dd7401c1f9ce.png

    Figure \(\PageIndex{34}\)

    74. Given the circuit in Figure \(\PageIndex{34}\), use either mesh or nodal analysis to determine \(v_{ed}\). \(E_1 = 9\angle 0^{\circ}\), \(E_2 = 12\angle 0^{\circ}\), \(I = 50E−3\angle 0^{\circ}\).

    75. Given the circuit in Figure \(\PageIndex{35}\), use mesh analysis to determine \(v_{fc}\). \(E_1 = 12\angle 0^{\circ}\), \(E_2 = 48\angle 0^{\circ}\), \(E_3 = 36\angle 70^{\circ}\).

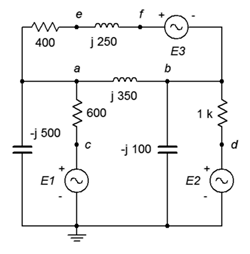
    clipboard_e1e1480ac90b3375c2519282727e1e835.png

    Figure \(\PageIndex{35}\)

    76. Find voltage \(v_{bc}\) in the circuit of Figure \(\PageIndex{36}\) using either mesh or nodal analysis. \(E = 100\angle 0^{\circ}\), \(R_1 = R_2 = 2\) k\(\Omega\), \(R_3\) = 3 k\(\Omega\), \(R_4\) = 10 k\(\Omega\), \(R_5\) = 5 k\(\Omega\), \(X_{C1} = X_{C2} = −j2\) k\(\Omega\).

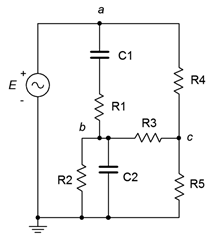
    clipboard_eb11902c92bad1ad8f7136de49e07eff9.png

    Figure \(\PageIndex{36}\)

    77. Given the circuit in Figure \(\PageIndex{37}\), use nodal analysis to find \(v_{ac}\). \(I_1 = 8E−3\angle 0^{\circ}\), \(I_2 = 12E−3\angle 0^{\circ}\), \(E = 50\angle 0^{\circ}\).

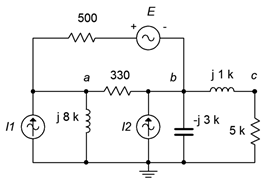
    clipboard_e43fafcccd342c6a1266f8a425f1aab2a.png

    Figure \(\PageIndex{37}\)

    78. Given the circuit in Figure \(\PageIndex{38}\), use nodal analysis to determine \(v_{ad}\). \(I_1 = 0.1\angle 0^{\circ}\), \(I_2 = 0.2\angle 0^{\circ}\), \(I_3 = 0.3\angle 0^{\circ}\).

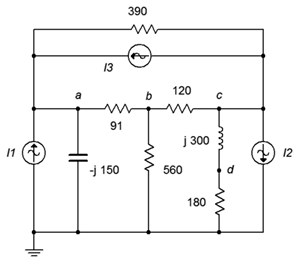
    clipboard_e691bafc16662feb96c8497c818f09d80.png

    Figure \(\PageIndex{38}\)

    79. Given the circuit in Figure \(\PageIndex{39}\), determine \(v_{ad}\). \(E_1 = 15\angle 0^{\circ}\), \(E_2 = 6\angle 0^{\circ}\), \(I = 100E−3\angle 0^{\circ}\).

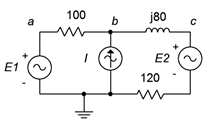
    clipboard_e46f0dd32a150b7273a32661564c83757.png

    Figure \(\PageIndex{39}\)

    80. Given the circuit in Figure \(\PageIndex{40}\), determine \(v_{ad}\). \(E_1 = 22\angle 0^{\circ}\), \(E_2 = −10\angle 0^{\circ}\), \(I = 2E−3\angle 0^{\circ}\).

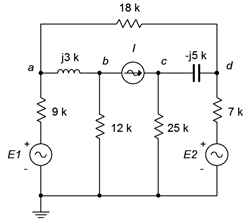
    clipboard_efc9f181935f99a5042d2c5101c10fca0.png

    Figure \(\PageIndex{40}\)

    81. Given the circuit in Figure \(\PageIndex{41}\), determine \(v_{ab}\). \(I_1 = 1.2\angle 0^{\circ}\), \(I_2 = 2\angle 120^{\circ}\), \(E = 75\angle 0^{\circ}\).

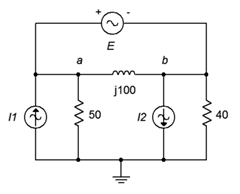
    clipboard_ec0b0a50ce561191f93eee140f5bcee41.png

    Figure \(\PageIndex{41}\)

    82. Given the circuit in Figure \(\PageIndex{42}\), determine \(v_{ad}\). \(I_1 = 0.8\angle 0^{\circ}\), \(I_2 = 0.2\angle 180^{\circ}\), \(I_3 = 0.1\angle 0^{\circ}\), \(E = 15\angle 0^{\circ}\).

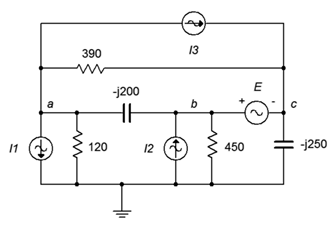
    clipboard_e51ab5d858075bfcd368a72e5c039a927.png

    Figure \(\PageIndex{42}\)

    Simulation

    83. Perform a transient analysis simulation on the circuit of problem 25 (Figure \(\PageIndex{16}\)) to verify the results for \(v_b\).

    84. Investigate the variation of \(v_b\) due to frequency in problem 25 (Figure \(\PageIndex{16}\)) by performing an AC simulation. Run the simulation from 10 Hz up to 100 kHz.

    85. Investigate the variation of \(v_b\) due to component tolerance in problem 25 (Figure \(\PageIndex{16}\)) by performing a Monte Carlo simulation. Apply a 10% tolerance to the resistors and capacitor.

    86. Perform a transient analysis simulation on the circuit of problem 28 (Figure \(\PageIndex{10}\)) to verify the results for \(v_c\).

    87. Investigate the variation of \(v_b\) due to frequency in problem 28 (Figure \(\PageIndex{10}\)) by performing an AC simulation. Run the simulation from 1 Hz up to 10 kHz.

    88. Investigate the variation of \(v_b\) due to component tolerance in problem 28 (Figure \(\PageIndex{10}\)) by performing a Monte Carlo simulation. Apply a 10% tolerance to the resistors and capacitors.

    This page titled 6.6: Exercises is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by James M. Fiore via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      James M. Fiore
      License
      CC BY-NC-SA
      License Version
      4.0
      Show TOC
      no
    2. Tags
      1. source@http://www.dissidents.com/resources/ACElectricalCircuitAnalysis.pdf