1.30: Potential barriers and Tunneling

Next we consider electrons incident on a potential barrier, as shown in Figure 1.30.1.

Figure \(\PageIndex{1}\): A potential barrier.

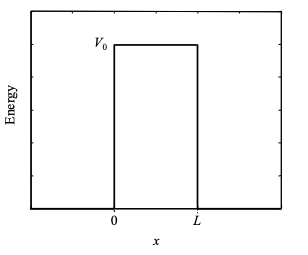
We will assume that the particle is incident on the barrier from the left. It has some probability of being reflected by the barrier. But it also has some probability of being transmitted even though its energy may be less than the barrier height. Transmission through a barrier is known as tunneling. There is no equivalent process in classical physics – the electron would need sufficient energy to jump over the barrier.

Once again, we solve the time-independent Schrödinger Equation. To the left and right of the barrier, the electron is in a classically allowed region. We model the electron in these regions by a plane wave; see Equation (1.25.3) and the associated discussion. On the other hand, within the barrier, if the energy, E, of the electron is below the barrier potential, \(V_{0}\), the barrier is a classically forbidden region. The solution in this region is described by expanding and decaying exponentials; see Equation (1.25.6) and the associated discussion.

Analyzing the potential piece by piece, we assume a solution of the form

\[ \psi(x)=\left\{\begin{array}{ll}
e^{i k x}+r e^{-i k x} & \text { for } x \leq 0 \\
a e^{\alpha x}+b e^{-\alpha x} & \text { for } 0 \leq x \leq L \\
t e^{i k x} & \text { for } x \geq L
\end{array}\right. \nonumber \]

where once again

\[ k =\sqrt{\frac{2mE}{\hbar^{2}}} \nonumber \]

and

\[ \alpha = \sqrt{\frac{2m(V_{0}-E)}{\hbar^{2}}} \nonumber \]

The intensity of the incoming plane wave is unity. Hence the amplitude of the reflected wave, r, is the reflection coefficient and the amplitude of the transmitted wave, t, is the transmission coefficient. (The reflectivity and transmissivity is \(|r|^{2}\) and \(|t|^{2}\), respectively).

Next we match the piecewise solutions at the left edge of the barrier. Equating the amplitude of the wavefunction gives

\[ \psi(0)=1+r=a+b \nonumber \]

Equating the slope of the wavefunction gives

\[ \psi’(0)=ik+ikr=\alpha a-\alpha b . \nonumber \]

At the right edge of the barrier, we have

\[ \psi(L)=a e^{\alpha L}+ b e^{-\alpha L}=te^{ikL} \nonumber \]

and

\[ \psi’(L)=a\alpha e^{\alpha L}- b\alpha e^{-\alpha L}=ikte^{ikL} \nonumber \]

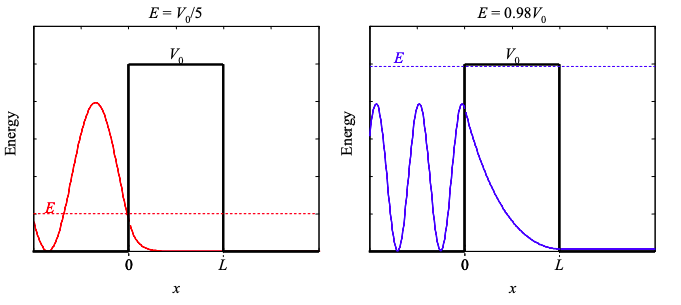
Thus, we have four simultaneous equations. But these are a pain to solve analytically. In Figure 1.30.2 we plot solutions for energy much less than the barrier, and energy close to the barrier. It is observed that the tunneling probability is greatly enhanced when the incident electron has energy close to the barrier height. Note that the wavefunction decay within the barrier is much shallower when the energy of the electron is large. Note also that the reflection from the barrier interferes with the incident electron creating an interference pattern.

When the electron energy is much less than the barrier height we can model the wavefunction within the barrier as simply a decaying exponential. The transmission probability is then approximately

\[ T \approx \text{exp}[-2 \alpha L] \nonumber \]

Figure \(\PageIndex{2}\): Plots of the wavefunction for an electron incident from the left. (a) When the electron energy is substantially below the barrier height, tunneling is negligible. (b) For an electron energy 98% of the barrier height, however, note the non-zero transmission probability to the right of the barrier.