3.5: Calculation of the electrostatic capacitance
- Page ID
- 50027
Isolated point conductors
For small conductors like single molecules or quantum dots, it is sometimes convenient to calculate \(C_{ES}\) by assuming that the conductor is a sphere of radius R. From Gauss's law, the potential at a point with radius r from the center of the sphere is:
\[ V = \frac{Q}{4\pi \epsilon r} \nonumber \]
where r > R, \(\epsilon\) is the dielectric constant and Q is the net charge on the sphere.
If we take the potential at infinity to be zero, then the potential of the sphere is \(V = Q/4\pi \epsilon R\) and the capacitance is
\[ C_{ES} = \frac{Q}{V} = 4\pi \epsilon R \nonumber \]
The notable aspect of Equation (3.5.2) is that the electrostatic capacitance scales with the size of the conductor. Consequently, the charging energy of a small conductor can be very large. For example, Equation (3.5.2) predicts that the capacitance of a sphere with a radius of R = 1nm is approximately \(C_{ES}=10^{-19}F\). The charging energy is then \(U_{C} = 1.6eV\) per charge.
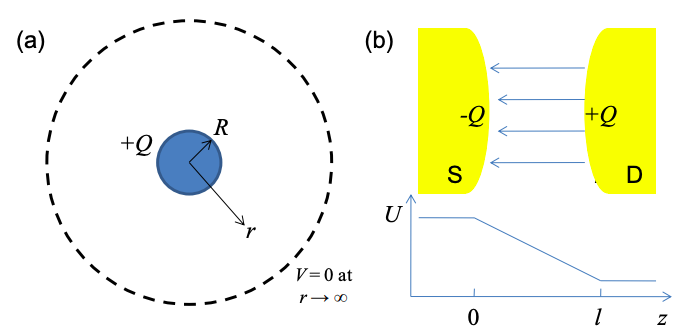
Conductors positioned between source and drain electrodes
In general, the potential profile for an arbitrary distribution of charges must be calculated using Gauss's law. But we can often make some approximations. The source and drain contacts can sometimes be modeled as a parallel plate capacitor with
\[ C = \frac{\epsilon A}{d} \nonumber \]
where A is the area of each contact and d is their separation. This approximation is equivalent to assuming a uniform electric field between the source and drain electrodes. This is valid if A \gg d and there is no net charge between the contacts. For source and drain electrodes separated by a distance l, the source and drain capacitances at a distance z from the source are:
\[ C_{S}(z) = \frac{\epsilon A}{z}, \ C_{D}(z) = \frac{\epsilon A}{l - z} . \nonumber \]
The potential varies linearly as expected for a uniform electric field.
\[ U(z) = -qV_{DS} \frac{1/C_{s}(z)}{1/C_{D}(z)+1/C_{S}(z)} = -qV_{DS}\frac{z}{l} \nonumber \]