6.8: Polyacetylene

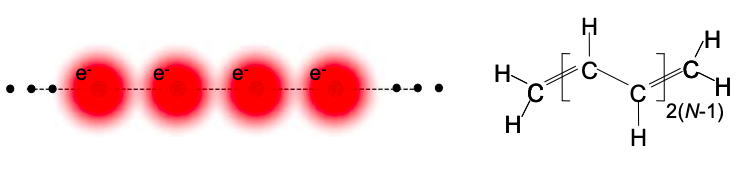
Next, let's consider a longer chain of carbon atoms. Very long molecules are known as polymers, and a polymer equivalent of the idealized conductor in Figure \(\PageIndex{1}\) is known as polyacetylene.

Figure \(\PageIndex{1}\): (left) An infinite chain of atoms each contributing a single electron in a frontier orbital. (right) The equivalent polymer polyacetylene.

Specifically, let's solve for a carbon chain of N atoms. Equation (6.8.11) is an example of a tridiagonal determinant. In general, an N × N tridiagonal determinant has eigenvalues:\(^{†}\)

\[ E_{n}= \alpha+2\beta \cos\left( \frac{n\pi}{N+1}\right), n = 1,2,…N. \nonumber \]

and eigenvectors:

\[ c_{j} = \sin\left( jn\frac{\pi}{N+1} \right), \ \ j, n = 1,2,… N. \nonumber \]

Note that Equations. (6.9.1)-(6.9.2) reduce to Equations. (6.8.11)-(6.8.12) by using the identity: \(\cos\left(2\pi/5\right)=1/4\left(-1+\sqrt{5}\right)\)

Thus, we have solved for the molecular orbitals in a molecule modeled by an arbitrarily long chain of frontier atomic orbitals, each containing a single electron.

Next, let's re-express our solutions for polyacetylene in terms of a wavevector, k. Note that because the atoms are discretely positioned in a chain, k is also discrete. There are only N allowed values of k.

Given \(x = ja_{0}\), where \(a_{0}\) is the spacing between carbon atoms, we get:

\[ c(x) = \sin(kx) \nonumber \]

and

\[ E_{n} = \alpha+2\beta \cos(ka_{0}) \nonumber \]

where

\[ k = \frac{\pi}{a_{0}} \frac{n}{N+1}, \ \ n=1,2,…N \nonumber \]

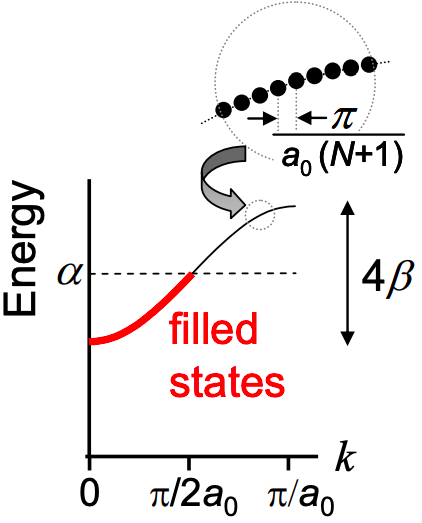
The dispersion relation of polyacetylene is plotted in Figure 6.9.2. The energy states are restricted to energies \[ E = \alpha \pm 2\beta , \nonumber \] forming a band, of width \(4\beta\), centered at \(\alpha\). The bandwidth (\(4\beta\)) is directly related to the hopping interaction between neighboring carbon atoms. This is a general property: the stronger the interaction between an electron and the neighboring atoms, the larger the bandwidth. And as we shall, the broader the electronic bandwidth, the better the electron conduction within the material.

There are N states in the band, each separated by

\[ \Delta k = \frac{\pi}{a_{0}(N+1)} \nonumber \]

Note that the length of the chain is \(L = (N-1)a_{0}\). Thus for long chains the separation between states in the band is approximately

\[ \Delta k \approx \frac{\pi}{L} \nonumber \]

Now each carbon atom contributes a single electron in the frontier atomic orbitals that comprise the molecular orbitals. Thus for a N-repeat polymer, there are N electrons. But each state holds two electrons, one of each spin. Filling the lowest energy states first, only the first N/2 k states are filled; see Fig. 6.17. Thus, the band is only half full, and so, if the polymer was connected to contacts we might expect polyacetylene to be a metal.

Figure \(\PageIndex{2}\): The dispersion relation of polyacetylene as determined by a tight binding analysis. For N atoms, each donating a single electron in a frontier atomic orbital, there are N molecular orbitals with energies arranged in a band. Since the band of states is only half full this material might be expected to be a metal.

\(^{†}\)If you are interested and have a few spare hours you can try to prove this. After evaluating the first few determinants of simple triadiagonal matrices, N=1, N=2, N=3, etc.. find and solve a difference equation for the determinants as a function of the matrix dimension, N.