6.14: Bloch functions- wavefunctions in periodic molecules
- Page ID
- 52347
Wavefunctions in periodic materials are described by Bloch functions. To better understand their properties, it is instructive for us to derive Bloch functions.\(^{†}\)
First, let's consider a periodic molecule, comprised of unit cells translated by multiples of the primitive lattice vectors. Let the wavefunction of the unit cell be \(\phi_{0}\). Under the tight binding approximation, the wavefunction of the unit cell is itself constructed from a linear combination of frontier atomic orbitals.
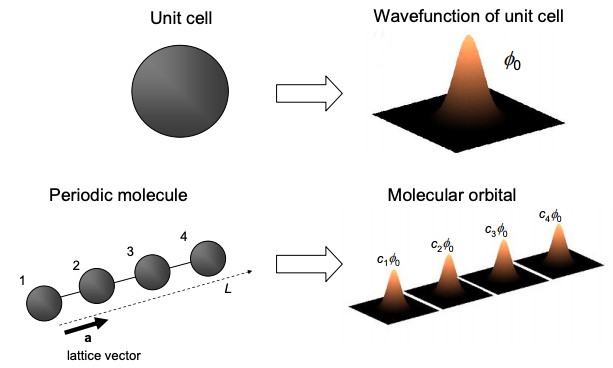
Now, the molecular orbitals will be composed of linear combinations of the wavefunction of the unit cell, i.e.
\[ \Psi = \sum_{r} c_{r}\phi_{0} \nonumber \]
where once again \(c_{r}\) is a set of coefficients. Note that, unlike approximations of molecular orbitals using linear combinations of frontier atomic orbitals, Equation (6.15.1) is exact. We emphasize that \(\phi_{0}\) in Equation (6.15.1) is the exact wavefunction of a unit cell of the complete molecule. In molecular orbital calculations \(\phi_{0}\) is typically calculated using tight binding, or another approximate technique. But for the moment we will assume that we know it exactly.
The aim of this derivation is to determine the coefficients cr given that the material is periodic. Quite generally, we can relate the two coefficients \(c_{1}\) and \(c_{2}\) of the first two unit cells by
\[ c_{2} =\alpha c_{1} \nonumber \]
where \(\alpha\) is some constant.
The symmetry of the material allows us to translate indistinguishably and consequently,
\[ c_{r+1} =\alpha c_{r} \nonumber \]
where 0 < r < N, where N is the number of unit cells in the material.
Now if we assume periodic boundary conditions, we can compare the identical unit cells at r and r + N:

\[ c_{N+1} =\alpha^{N} c_{1} \nonumber \]
But since \(c_{N+1} = c_{1}\), \(\alpha\) must be one of N roots of unity, i.e. \(\alpha = \text{exp}[i2\pi n/N]\), where n is an integer. Thus, the coefficients are phase factors; the wavefunction corresponding to each unit cell is modulated by a phase factor in a periodic molecule. Consequently, if we set \(c_{N} = 1\) (which we can do since absolute phase is arbitrary):
\[ c_{r}=e^{i\frac{2\pi n}{N}r} \nonumber \]
Alternately, approximating the coefficients by a continuous function, we can write:
\[ c(x)=e^{ikx} \nonumber \]
where
\[ \frac{2\pi n}{L} \nonumber \]
Once again, only certain k values are allowed by the application of periodic boundary conditions. After all, standing waves in the molecule can possess only certain wavelengths. Recall also that Fourier transforms of periodic signals are discrete; see Figure 6.16.1. Thus, it follows from a Fourier analysis of the coefficients that k must be discrete. In addition, the Fourier transform of the coefficients is itself periodic since the coefficients are discrete (recall discrete time Fourier series - DTFS).
\(^{†}\)Our method follows the derivation of Kittel in "Introduction to Solid State Physics", Wiley, 7th Edition, 1996.

