5.16: Exercises

1. The Thevenin equivalent output impedance of each of the amplifiers in Figure 5.12.8(a) is \(5\:\Omega\), and the system impedance, \(R_{0}\), is \(75\:\Omega\). Choose the transformer windings for maximum power transfer. [Parallels Example 5.12.4]
2. A spiral inductor is modeled as an ideal inductor of \(10\text{ nH}\) in series with a \(5\:\Omega\) resistor. What is the \(Q\) of the spiral inductor at \(1\text{ GHz}\)?
3. Consider the design of a \(50\text{ dB}\) resistive \(\mathsf{T}\) attenuator in a \(75\:\Omega\) system. [Parallels Example 5.5.1]
   1. Draw the topology of the attenuator.
   2. Write down the design equations.
   3. Complete the design of the attenuator.
4. Consider the design of a \(50\text{ dB}\) resistive Pi attenuator in a \(75\:\Omega\) system. [Parallels Example 5.5.1]
   1. Draw the topology of the attenuator.
   2. Write down the design equations.
   3. Complete the design of the attenuator.
5. A \(20\text{ dB}\) attenuator in a \(17\:\Omega\) system is ideally matched at both the input and output. Thus there are no reflections and the power delivered to the load is reduced by \(20\text{ dB}\) from the applied power. If a \(5\text{ W}\) signal is applied to the attenuator, how much power is dissipated in the attenuator?
6. A resistive Pi attenuator has shunt resistors of \(R_{1} = R_{2} = 294\:\Omega\) and a series resistor \(R_{3} = 17.4\:\Omega\). What is the attenuation (in decibels) and the characteristic impedance of the attenuator?
7. A resistive Pi attenuator in a system with characteristic impedance \(Z_{0}\) has equal shunt resistors of \(R_{1} = R_{2}\) and a series resistor \(R_{3}\). Show that \(Z_{0} = \sqrt{(R_{1}^{2}R_{3})/(2R_{1} + R_{3})}\) and the attenuation factor \(K = \sqrt{(R_{1} + Z_{0})/(R_{1} − Z_{0})}\). [Start with Equation (5.5.2).]
8. Design a resistive Pi attenuator with an attenuation of \(10\text{ dB}\) in a \(100\:\Omega\) system.
9. Design a \(3\text{ dB}\) resistive Pi attenuator in a \(50\:\Omega\) system.
10. A resistive Pi attenuator has shunt resistors \(R_{1} = R_{2} = 86.4\:\Omega\) and a series resistor \(R_{3} = 350\:\Omega\). What is the attenuation (in decibels) and the system impedance of the attenuator?
11. Derive the \(50\:\Omega\) scattering parameters of the ideal transformer shown below where the number of windings on the secondary side (Port \(\mathsf{2}\)) is twice the number of windings on the primary side (Port \(\mathsf{1}\)).

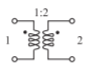
Figure \(\PageIndex{1}\)

1. What is \(S_{11}\)? [Hint: Terminate Port \(\mathsf{2}\) in \(50\:\Omega\) and determine the input reflection coefficient.]
2. What is \(S_{21}\)?
3. What is \(S_{22}\)?
4. What is \(S_{12}\)?

12. Derive the two-port \(50\:\Omega\) scattering parameters of the magnetic transformer below. The primary (Port \(\mathsf{1}\)) has \(10\) turns, the secondary (Port \(\mathsf{2}\)) has \(25\) turns.

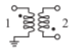
Figure \(\PageIndex{2}\)

1. What is \(S_{11}\)?
2. What is \(S_{21}\)?
3. What is \(S_{22}\)?
4. What is \(S_{12}\)?

13. An ideal quadrature hybrid has the scattering parameters
    \[S_{90^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{-\jmath}&{1}&{0}\\{-\jmath}&{0}&{0}&{1}\\{1}&{0}&{0}&{-\jmath}\\{0}&{1}&{-\jmath}&{0}\end{array}\right]\nonumber \]
    Draw the signal flow graph of the hybrid, labeling each of the edges and assigning \(a_{1},\: b_{1},\) etc., to the nodes. (Do not start with the SFG of a generic 4-port network.)
14. An ideal \(180^{\circ}\) hybrid has the scattering parameters
    \[S_{180^{\circ}}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}{0}&{1}&{-1}&{0}\\{1}&{0}&{0}&{1}\\{-1}&{0}&{0}&{1}\\{0}&{1}&{1}&{0}\end{array}\right]\nonumber \]
    Draw the signal flow graph of the hybrid, labeling each of the edges and assigning \(a_{1},\: b_{1},\) etc., to the nodes. (Note, do not start with the SFG of a generic 4-port network.)
15. A signal is applied to Ports \(\mathsf{2}\) and \(\mathsf{3}\) of a \(180^{\circ}\) hybrid, as shown in Figure 5.8.2(b). If the signal consists of a differential component of \(0\text{ dBm}\) and a common mode component of \(10\text{ dBm}\):
    1. Determine the power delivered at Port \(\mathsf{1}\).
    2. Determine the power delivered at Port \(\mathsf{4}\). Assume that the hybrid is lossless.
16. Silicon RFICs use differential signal paths to minimize the introduction of substrate noise. As well, differential amplifiers are an optimum topology in current-biased circuits. Off-chip signals are often on microstrip lines and so the source and load, being off-chip, are not differential. The off-chip circuits are then called single-ended. Using \(180^{\circ}\) hybrids, diagrams, and explanations, outline a system architecture accommodating this mixed differential and single-ended environment.
17. Consider the hybrid shown in the figure below. If the number of windings of Coils \(\mathsf{2}\) and \(\mathsf{3}\) are twice the number of windings of Coil \(\mathsf{1}\), show that for matched hybrid operation \(2Z_{2} = Z_{3} = 8Z_{0}\).

Figure \(\PageIndex{3}\)

18. The balun of Figure 5.9.3 transforms an unbalanced system with a system impedance of \(Z_{0}\) to a balanced system with an impedance of \(4Z_{0}\). The actual impedance transformation is determined by the number of windings of the coils. Design a balun of the type shown in Figure 5.9.3 that transforms an unbalanced \(50\:\Omega\) system to a balanced \(377\:\Omega\) system. [Hint: Find the ratio of the windings of the coils.]
19. A balun can be realized using a wire-wound transformer, and by changing the number of windings on the transformer it is possible to achieve impedance transformation as well as balanced-to-unbalanced functionality. A \(500\text{ MHz}\) balun based on a magnetic transformer is required to achieve impedance transformation from an unbalanced impedance of \(50\:\Omega\) to a balanced impedance of \(200\:\Omega\). If there are \(20\) windings on the balanced port of the balun transformer, how many windings are there on the unbalanced port of the balun?
20. Design a lumped-element two-way power splitter in a \(75\:\Omega\) system at \(1\text{ GHz}\). Base your design on a Wilkinson power divider.
21. Design a three-way power splitter in a \(75\:\Omega\) system. Base your design on a Wilkinson power divider using transmission lines and indicate lengths in terms of wavelengths.
22. Design a lumped-element three-way power splitter in a \(75\:\Omega\) system at \(1\text{ GHz}\). Base your design on a Wilkinson power divider.
23. A resistive power splitter is a three-port device that takes power input at Port \(\mathsf{1}\) and delivers power at Ports \(\mathsf{2}\) and \(\mathsf{3}\) that are equal; that is, \(S_{21} = S_{31}\). However, the sum of the power at Ports \(\mathsf{2}\) and \(\mathsf{3}\) will not be equal to the input power due to loss. Design a \(75\:\Omega\) resistive three-port power splitter with matched inputs, \(S_{11} =0= S_{22} = S_{33}\). That is, draw the resistive circuit and calculate its element values.
24. Design a balun based on a magnetic transformer if the balanced load is \(300\:\Omega\) and the unbalanced impedance is \(50\:\Omega\).
    1. Draw the schematic of the balun with the load and indicate the ratio of windings.
    2. If the number of windings on the unbalanced side of the transformer is \(20\), how many windings are on the unbalanced side?
25. Develop the electrical design of a rat-race hybrid at \(30\text{ GHz}\) in a \(50\:\Omega\) system.
26. Develop the electrical design of a rat-race hybrid at \(30\text{ GHz}\) in a \(100\:\Omega\) system.
27. Design a lumped-element \(180^{\circ}\) hybrid at \(1900\text{ MHz}\) using \(1\text{ nH}\) inductors.
28. Design a \(90^{\circ}\) lumped-element hybrid at \(1900\text{ MHz}\) using \(1\text{ nH}\) inductors.
29. Design a \(90^{\circ}\) lumped-element hybrid at \(500\text{ MHz}\) for a \(75\:\Omega\) system.
30. Design a lumped-element \(180^{\circ}\) hybrid at \(1900\text{ MHz}\) matched to \(50\:\Omega\) source and load impedances.

5.16.1 Exercises by Section

\(†\)challenging, \(‡\)very challenging

\(§5.1\: 1\)

\(§5.2\: 2, 3, 4, 5\)

\(§5.5\: 6†, 7†, 8, 9, 10†\)

\(§5.8\: 11†, 12†\)

\(§5.9\: 13†, 14†, 15†, 16†, 17‡\)

\(§5.10\: 18†, 19†\)

\(§5.11\: 20†, 21†, 22†\)

\(§5.12\: 23†\)

\(§5.13\: 24‡, 25†, 26†, 27, 28, 29, 30\)

5.16.2 Answers to Selected Exercises

2. \(12.57\)
3. \(R_{1}=R_{2}=74.5\:\Omega\)
4. \(75.48\:\Omega\)
5. \(4.95\text{ W}\)

11. (c) \(0.6\)
12. \(-0.6897\)

15. \(10\text{ dBm}\)

Figure \(\PageIndex{4}\)

\(L=20.7\text{ nH}\), \(C_{1}=3.68\text{ pF}\)

\(C_{2}=1.23\text{ pF}\), \(R=75\:\Omega\)

24. ratio of windings is \(2.45\)

30. Fig 5.13.3(a)
    \(L=5.92\text{ nH}\), \(C=1.19\text{ pF}\)