7.2: Fano-Bode Limits

Last updated
Save as PDF

Page ID: 41144

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

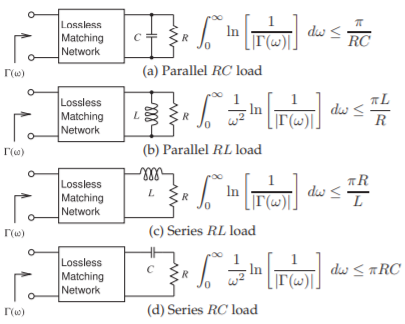
Figure \(\PageIndex{1}\): Fano-Bode limits for circuits with reactive loads.

Figure \(\PageIndex{2}\): Response looking into matching network used in defining nonintegral Fano-Bode criteria. The bandwidth of the passband (low \(\Gamma\), is BW).

A complex load having energy storage elements limits the bandwidth of the match achieved by a matching network. Theoretical limits addressing the bandwidth and the quality of the match were developed by Fano [1, 2] based on earlier work by Bode [3]. These theoretical limits are known as the FanoBode criteria or the Fano-Bode limits. The limits for simple loads are shown in Figure \(\PageIndex{1}\). More general loads are treated by Fano [1]. The Fano-Bode criteria are used to justify the broad assertion that the more reactive energy stored in a load, the narrower the bandwidth of a match.

The Fano-Bode criteria include the term \(1/ |\Gamma (\omega )|\), which is the inverse of the magnitude of the reflection coefficient looking into the matching network, as shown in Figure \(\PageIndex{1}\). A matching network provides matching over a radian bandwidth BW, and outside the matching frequency band the magnitude of the reflection coefficient approaches \(1\). Introducing \(\Gamma_{\text{avg}}\) as the average absolute value of \(\Gamma (\omega )\) within the passband, and with \(f_{0} = \omega_{0}/(2\pi )\) as the center frequency of the match (see Figure \(\PageIndex{2}\)), then the four Fano-Bode criteria shown in Figure \(\PageIndex{1}\) can be written as

Parallel RC load:

\[\label{eq:1}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\frac{\pi}{R(\omega_{0}C)} \]

Parallel RL load:

\[\label{eq:2}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\frac{\pi(\omega_{0}L)}{R} \]

Series RL load:

\[\label{eq:3}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\frac{\pi R}{(\omega_{0} L)} \]

Series RC load:

\[\label{eq:4}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\pi R(\omega_{0}C) \]

In terms of reactance and susceptance these can be written as

Parallel load:

\[\label{eq:5}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\frac{\pi G}{|B|} \]

Series load:

\[\label{eq:6}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\frac{\pi R}{|X|} \]

where \(G = 1/R\) is the conductance of the load, \(B\) is the load susceptance, and \(X\) is the load reactance. \(\text{BW}/\omega_{0}\) is the fractional bandwidth of the matching network. Equations \(\eqref{eq:5}\) and \(\eqref{eq:6}\) indicate that the greater the proportion of energy stored reactively in the load compared to the power dissipated in the load, the smaller the fractional bandwidth \((\text{BW}/\omega_{0})\) for the same average in-band reflection coefficient \(\Gamma_{\text{avg}}\).

Equations \(\eqref{eq:5}\) and \(\eqref{eq:6}\) can be simplified one step further:

\[\label{eq:7}\frac{\text{BW}}{\omega_{0}}\ln\left(\frac{1}{\Gamma_{\text{avg}}}\right)\leq\frac{\pi}{Q} \]

where \(Q\) is that of the load. Several general results can be drawn from Equation \(\eqref{eq:7}\) as follows:

If the load stores any reactive energy, so that the \(Q\) of the load is nonzero, the in-band reflection coefficient looking into the matching network cannot be zero across the passband.
The higher the \(Q\) of the load, the narrower the bandwidth of the match for the same average in-band reflection coefficient.
The higher the \(Q\) of the load, the more difficult it will be to design the matching network to achieve a specified matching bandwidth.
A match over all frequencies is only possible if the \(Q\) of the load is zero; that is, if the load is resistive. In this case a resistive load could be matched to a resistive source by using a magnetic transformer. Using a matching network with lumped \(L\) and \(C\) components will result in a match over a finite bandwidth. However, with more than two \(L\) and \(C\) elements the bandwidth of the match can be increased.
Multielement matching networks are required to maximize the matching network bandwidth and minimize the in-band reflection coefficient. The matching network design becomes more difficult as the \(Q\) of the load increases.