3.16: SDR Quadrature Modulators
- Page ID
- 41202
The SDR transmitter uses two-stage modulation with DSB-SC modulation implemented in DSP to produce an IF signal which is output using DACs to produce analog I and Q channel IF signals. These IF signals are then input to an analog quadrature modulator implementing SSB-SC modulation with the resulting radio signal being a DSB-SC radio signal. As of the time of this writing the digital portion was implemented in what is called a baseband chip and the analog portion implemented in an RF modem chip. One can expect that eventually these would be combined into a single chip. As far as the RF modem chip is concerned, the IF signals input to the up-converter are baseband signals and this is how they are often referred to when the focus is on the RF modem chip.
Quadrature modulation, see Figure 3.8.1, comprises two mixer cores which are driven by a modulating in-phase component \(i(t)\) and a modulating quadrature-phase component \(q(t)\) where in-phase and quadrature phase refer to the phase of the local oscillator input to the mixer cores. Here \(i(t)\) and \(q(t)\) are baseband signals with a spectrum extending from (near) DC to \(f_{\text{BB}}\) and in today’s radios they are produced internally in a DSP unit. The finite bandwidth \(i(t)\) and \(q(t)\) signals contain \(I\)-channel and \(Q\)-channel information respectively. The top mixer core is driven directly by the local oscillator and the other, the quadrature mixer core, is also driven by the local oscillator but now it is phase shifted by \(90^{\circ}\), i.e. it is in quadrature. This scheme produces double-sideband suppressed carrier DSB-SC modulation and \(s(t)\) is the modulated output signal with each sideband having bandwidth \(f_{\text{BB}}\). The block-level schematic illustrates the basic architecture of a quadrature modulator which is expanded if the signals are differential signals with additional variations according to whether the mixers are implemented as analog multipliers or as switches controlled by the LO. The whole structure shown is referred to as a mixer and each mixer core on its own is also often referred to as a mixer. This operation can be implemented without error in DSP.
3.9.1 Analog Quadrature Modulator
The second stage of an SDR transmitter implements DSB-SC modulation using analog circuitry producing an RF signal.
An analog quadrature modulator using multipliers is shown in Figure \(\PageIndex{1}\)(a) and consists of two multipliers each of which has two inputs and one output with the outputs summed yielding a modulated output signal \(s(t)\). One particular characteristic of a quadrature modulator is that the LO at frequency \(f_{\text{LO}}\) is directly input to one of the multipliers but the second multiplier is driven by a version of the LO with a \(90^{\circ}\) phase lag, i.e. the LO input to the first mixer is in-phase and the LO input to the second multiplier has quadrature-phase (the phase is shifted by \(90^{\circ}\)). This second LO is also called the quadrature LO. The \(90^{\circ}\) phase difference of the two LOs is where the quadrature in quadrature modulator comes from. So if the LO is \(\sin(2πf_{\text{LO}})\), \(i(t)\) is multiplied by \(\sin(2πf_{\text{LO}})\). Then \(q(t)\) is multiplied by \(\sin(2πf_{\text{LO}} − π/2) = − \cos(2πf_{\text{LO}})\). The second inputs of the multipliers in Figure \(\PageIndex{1}\)(a) are the signals \(i(t)\) and \(q(t)\) with \(i\) indicating that the signal is driving the in-phase multiplier and \(q\) indicating that the signal is driving the quadrature-phase multiplier. The signals \(i(t)\) and \(q(t)\) may be independent, or the frequency components of \(q(t)\) may phase lag \(i(t)\) by \(90^{\circ}\) but otherwise be the same as \(i(t)\). These two options yield modulated output signals with different bandwidths.
Transistor-Based Multiplier
There are several ways to implement the mixer core in Figure \(\PageIndex{1}\)(a) with the most common being as a multiplier or as a switch. Both can be conveniently implemented using transistors. The analog multiplier shown in Figure \(\PageIndex{1}\)(b) is based on a cascode amplifier with one input applied to the gate of transistor \(\text{M}_{1}\). Instead of the gate of \(\text{M}_{2}\) being held at a DC voltage as with a cascode amplifier, the gate of \(\text{M}_{2}\) is also an input. Approximately, the drain current, \(I_{D}\), of \(\text{M}_{1}\) is proportional to the gate voltage \(v_{\text{IF}}\) and the voltage gain of \(\text{M}_{2}\), i.e. \(v_{\text{RF}}/v_{\text{LO}}\) is proportional to \(I_{D}\). Thus the RF output voltage \(v_{\text{RF}}\) is proportional to the product of \(v_{\text{IF}}\) (which in the modulator is either \(i(t)\) or \(q(t)\)) and \(v_{\text{LO}}\). So when \(v_{\text{IF}}\) and \(v_{\text{LO}}\) are sinewaves the output \(v_{\text{LO}}\) will be the trigonometric expansion of the product of two sinewaves and this product will also comprise two sinewaves at the sum and difference frequencies. Then circuit symmetry is used to select just one of these.
Polyphase Filter
A polyphase filter, such as the one-stage polyphase filter in in Figure \(\PageIndex{1}\)(c), takes an input analog input signal and outputs two signals that are the same except that the frequency components are shifted by \(90^{\circ}\). This circuit can be used to produce the quadrature LO signal or to shift the frequency components of a baseband signal. More commonly a polyphase filter is
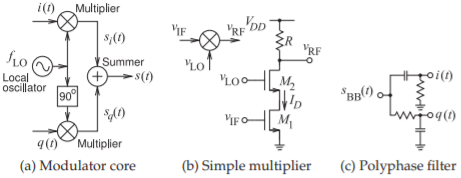
Figure \(\PageIndex{1}\): Quadrature modulator. The simple modulator in (b) is based on a FET cascode amplifier and the polyphase filter in (c) has a \(90^{\circ}\) phase difference between \(i(t)\) and \(q(t)\).
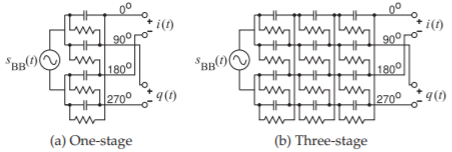
Figure \(\PageIndex{2}\): Differential polyphase filters.

Figure \(\PageIndex{3}\): Spectra of the baseband \(i(t)\) and \(q(t)\) signals and the modulated \(s(t)\) signal, see Figure \(\PageIndex{1}\)(a), for double sideband (DSB) and single sideband (SSB) suppressed-carrier (SC) modulation. Here the carrier frequency \(f_{c} = f_{\text{LO}}\), the LO frequency in Figure \(\PageIndex{1}\)(a).
realized in differential form as shown in Figure \(\PageIndex{2}\)(a). The polyphase filters in Figures \(\PageIndex{1}\)(c) and \(\PageIndex{2}\)(a) are narrowband but the bandwidth can be increased using more stages, see Figure \(\PageIndex{2}\)(b).
Double Sideband Modulation
When \(i(t)\) and \(q(t)\) are independent, effectively pseudo-random, signals the result is double sideband (DSB) modulation, see Figures \(\PageIndex{3}\)(a–d) with each sideband having the bandwidth of the baseband signals. The amplitude spectra of \(i(t)\) and \(q(t)\) will be the same as shown in Figure \(\PageIndex{3}\)(a) and each has a bandwidth \(f_{\text{BB}}\).\(^{1}\) As seen in Figure \(\PageIndex{3}\)(b) the frequency components of the \(i(t)\) spectrum are arbitrarily assigned a \(45^{\circ}\) phase. Since \(i(t)\) and \(q(t)\) are independent the phase of \(q(t)\) relative to the phase of \(i(t)\) is random, see Figure \(\PageIndex{3}\)(c). The modulated signal \(s(t)\) then has a sideband below the carrier frequency \(f_{c}\) and a sideband above \(f_{c}\), see Figure \(\PageIndex{3}\)(d), for a total bandwidth \(2f_{\text{BB}}\).
The multipliers in a quadrature modulator are implemented as mixer circuits and one type of mixer in particular is the multiplicative mixer shown in Figure \(\PageIndex{1}\)(a). Ideally a multiplicative mixer multiplies two sinewaves together to produce the trigonometric expansion of the product of two sinewaves. For example, \(\sin(A)\cdot \sin(B) = \frac{1}{2} [\cos(A − B) − \cos(A + B)]\). Following the signal paths in Figure \(\PageIndex{1}\)(a) and considering the frequency component \(A_{i}(f_{i}) \sin(\omega_{i}t)\) of \(i(t)\) at radian frequency \(\omega_{i} = 2πf_{i}\) and a frequency component \(A_{q}(f_{q}) \sin(\omega_{q}t)\) of \(q(t)\) at radian \(\omega_{q} = 2πf_{q}\) the modulated signal with the LO frequency replaced by \(f_{c}\) (with radian carrier frequency \(\omega_{c} = 2πf_{c}\)) is
\[\begin{align}s(t)&=s_{i}(t)+s_{q}(t)\nonumber \\ &=[A_{i}(f_{i})\sin(\omega_{i}t)\sin(\omega_{c}t)]+[A_{q}(f_{q})\sin(\omega_{q}t)\sin(\omega_{c}t-\pi /2)]\nonumber \\ &=[A_{i}(f_{i})\sin(\omega_{i}t)\sin(\omega_{c}t)]-[A_{q}(f_{q})\sin(\omega_{q}t)\cos(\omega_{c}t)]\nonumber \\&=\frac{1}{2}[A_{i}(f_{i})\cos(\omega_{c}-\omega_{i})t-A_{i}(f_{i})\cos(\omega_{c}+\omega_{i})t\nonumber \\ &\quad -A_{q}(f_{q})\sin(\omega_{c}+\omega_{q})t+A_{q}(f_{q})\sin(\omega_{c}-\omega_{q})t]\nonumber \\&=\frac{1}{2}[A_{i}(f_{i})\cos(\omega_{c}-\omega_{i})t+A_{q}(f_{q})\sin(\omega_{c}-\omega_{q})t] \nonumber \\ \label{eq:1}&\quad -\frac{1}{2}[A_{i}(f_{i})\cos(\omega_{c}+\omega_{i})t+A_{q}(f_{q})\sin(\omega_{c}+\omega_{q})t]\end{align} \]
The DSB-SC modulated signal is the signal in Equation \(\eqref{eq:1}\) summed for all \(f_{i}\) and \(f_{q}\) components from DC to \(f_{\text{BB}}\).
The expansion in Equation \(\eqref{eq:1}\) can be repeated for all of the frequency components of \(i(t)\) and \(q(t)\). So while the expansion is only performed for discrete frequencies, all that is necessary is that the multiplier be practically ideal, something that is typically achieved by an analog multiplier to better than \(1\%\). If the DSB-SC signal was produced digitally then multiplication can be precisely implemented and the DSB-SC modulation is ideal although the maximum frequency is limited by the capabilities of the digital circuitry. A DSP-based DSB-SC modulation has a low carrier frequency as keeping the (digital) carrier frequency low reduces DC power requirements. If \(i(t)\) and \(q(t)\) are independent, Equation \(\eqref{eq:1}\) indicates a lower modulated sideband at the range of frequencies \((f_{\text{LO}} −f_{i})\) and \((f_{\text{LO}} −f_{q})\) and an upper modulated sideband at the range of frequencies \((f_{\text{LO}} + f_{i})\) and \((f_{\text{LO}} + f_{q})\) for all \(f_{i}\) and \(f_{q}\) from \(0\) (DC) to \(f_{\text{BB}}\). That is, this is DSB-SC modulation, as seen in Figure \(\PageIndex{3}\)(d). In demodulation both sidebands are needed to recover \(i(t)\) and \(q(t)\).
Single Sideband Modulation
When \(i(t)\) and \(q(t)\) are the same signal except that every frequency component of \(q(t)\) is shifted by \(90^{\circ}\) the result is single sideband (SSB) modulation and the modulated output signal has a bandwidth \(f_{\text{BB}}\). The carrier itself does not exist in the output with a quadrature modulator using multipliers so this modulator implements SSB suppressed-carrier (SSB-SC) modulation. The modulated output signal is obtained with \(q(t) = A_{i}(f_{i}) \sin(\omega_{i} − π/2) = −A_{i}(f_{i}) \cos(\omega_{1})\). Then Equation \(\eqref{eq:1}\) becomes (but now \(f_{\text{LO}}\) is used to distinguish it from the carrier frequency which is defined by the characteristics of the modulating signal)
\[\begin{align} s(t)&=s_{i}(t)+s_{q}(t)\nonumber \\ &=[A_{i}(f_{i})\sin(\omega_{i}t)\sin(\omega_{\text{LO}}t)]-[A_{i}(f_{i})\cos(\omega_{i}t)\sin(\omega_{\text{LO}}t-\pi /2)]\nonumber \\ &=A_{i}(f_{i})[\sin(\omega_{i}t)\sin(\omega_{\text{LO}}t)+\cos(\omega_{i}t)\cos(\omega_{\text{LO}}t)] \nonumber \\ &=\frac{1}{2}A_{i}(f_{i})\{\cos[(\omega_{\text{LO}}-\omega_{i})t]-\cos[(\omega_{\text{LO}}+\omega_{i})t]\nonumber \\ &\quad +\cos[(\omega_{\text{LO}}+\omega_{i})t]+\cos[(\omega_{\text{LO}}-\omega_{i})t]\} \nonumber \\ \label{eq:2} &=A_{i}(f_{i})\cos [(\omega_{\text{LO}}-\omega_{i})]t\end{align} \]
Equation \(\eqref{eq:2}\) indicates that just the lower sideband is present and this is SSB-SC modulation as seen in Figure \(\PageIndex{3}\)(h) and the bandwidth of the modulated output signal is \(f_{\text{BB}}\). The original \(i(t)\) signal can be recovered from this one sideband but that is because \(q(t)\) contains exactly the same information as \(i(t)\) (although phase shifted).
If instead the phase of each frequency component of \(q(t)\) led the same frequency component of \(i(t)\) by \(+90^{\circ}\) then \(s(t)\) would comprise the upper sideband and this is still this would be SSB-SC modulation, see Figures \(\PageIndex{3}\)(i–l). For SSB-SC modulation each frequency component of \(q(t)\) must have a phase that differs from the corresponding component of \(i(t)\) by \(90^{\circ}\). A lumped-element circuit that realizes this is the polyphase filter, see Figure \(\PageIndex{1}\)(c), but the phase shift can also be realized in DSP.
Earlier, just before Equation \(\eqref{eq:2}\), it was stated that the frequency of the carrier was defined by the characteristics of the modulated signal which in turn depends on the characteristics of the modulating signal. This modulating signal, the \(i(t)\) input to the SSB-SC modulator, could also be modulated as is usually the case in SDR where DSB-SC modulation in done in a DSP and this is followed by SSB-SC modulation done at RF using analog hardware. Identifying the correct RF carrier is required for demodulation. In identifying the carrier there are two situations to consider. If the input, \(i(t)\), of the SSB-SC modulator is not modulated, e.g. it is just a baseband signal, then the carrier frequency is just the frequency of the LO of the SSBSC modulator as shown in Figure 3.10.1(a), i.e. \(f_{c} = f_{\text{LO}}\). If the input signal to the SSB-SC modulator is itself a DSB-SC signal (produced by a DSB-SC modulator) so that it has its own intermediate carrier frequency \(f_{c,\text{ IF}}\), then the carrier frequency \(f_{c} = f_{\text{LO}} − f_{c,\text{IF}}\). This situation is shown in Figure 3.10.1(b). (Note that the carrier frequency would be above \(f_{\text{LO}}\) if the frequency components of \(q(t)\) were advanced in phase by \(90^{\circ}\) relative to the phase of the frequency components of \(i(t)\).)
3.9.2 Summary
This section discussed quadrature modulation and showed how the same circuit can be used for DSB and for SSB modulation. The difference is in whether or not \(i(t)\) and \(q(t)\) are related. In modern radios DSB is implemented in DSP to produce an IF modulated signal with the spectra shown in Figure \(\PageIndex{3}\)(d) and \(f_{c}\) is very low, perhaps even \(f_{c} = f_{\text{BB}}\). Then this DSB-SC signal becomes the baseband of an analog SSB modulator that produces the RF modulated signal. This RF modulated signal is a DSB signal with a (suppressed) carrier in the middle of the spectrum.
Footnotes
[1] The short-term spectra will be different because \(i(t)\) and \(q(t)\) are different signals but over a long time interval the envelope of the amplitude spectra will become similar.


