4.9: Exercises

1. An antenna only radiates \(45\%\) of the power input to it. The rest is lost as heat. What input power (in \(\text{dBm}\)) is required to radiate \(30\text{ dBm}\)?
2. The output stage of an RF front end consists of an amplifier followed by a filter and then an antenna. The amplifier has a gain of \(27\text{ dB}\), the filter has a loss of \(1.9\text{ dB}\), and of the power input to the antenna, \(35\%\) is lost as heat due to resistive losses. If the power input to the amplifier is \(30\text{ dBm}\), calculate the following:
   1. What is the power input to the amplifier in watts?
   2. Express the loss of the antenna in \(\text{dB}\).
   3. What is the total gain of the RF front end (amplifier + filter)?
   4. What is the total power radiated by the antenna in \(\text{dBm}\)?
   5. What is the total power radiated by the antenna in \(\text{mW}\)?
3. The output stage of an RF front end consists of an amplifier followed by a filter and then an antenna. The amplifier has a gain of \(27\text{ dB}\), the filter has a loss of \(1.9\text{ dB}\), and of the power input to the antenna, \(45\%\) is lost as heat due to resistive losses. If the power input to the amplifier is \(30\text{ dBm}\), calculate the following:
   1. What is the power input to the amplifier?
   2. Express the loss of the antenna in decibels.
   3. What is the total gain of the RF front end (amplifier + filter)?
   4. What is the total power radiated by the antenna in \(\text{dBm}\)?
   5. What is the total power radiated by the antenna in milliwatts?
4. In the figure below there are two transmitters, \(\text{Tx}_{1}\) and \(\text{Tx}_{2}\), operating at the same power level, and one receiver, \(\text{Rx}\). \(\text{Tx}_{2}\) is an intentional transmitter and its signal is intended to be received at \(\text{Rx}\). \(\text{Tx}_{1}\) uses the same frequency channel as \(\text{Tx}_{2}\), but it transmits an interfering signal. [Parallels Example 4.1.1]

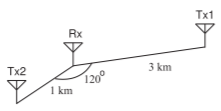
Figure \(\PageIndex{1}\)

1. Assume that the antennas are omnidirectional and, being in a semiurban area, that the transmitted power density drops off as \(1/d^{3}\), where \(d\) is the distance from the transmitter. Calculate the SIR at \(\text{Rx}\). Express your answer in decibels.
2. Now consider a directional antenna at \(\text{Rx}\) while the transmit antennas remain omnidirectional. The antenna at \(\text{Rx}\) is directed toward the transmitter \(\text{Tx}_{2}\) and the antenna gain is \(6\text{ dB}\). In the direction of \(\text{Tx}_{1}\) the effective antenna gain is \(−3\text{ dB}\). Now recalculate the SIR. Express your answer in \(\text{dB}\).

5. Thirty five percent of the power input to an antenna is lost as heat, what is the loss of the antenna in \(\text{dB}\).
6. Only \(65\%\) of the power input to an antenna is radiated with the rest lost to dissipation in the antenna, what is the gain of the antenna in \(\text{dB}\)? (This is not the antenna gain.)
7. The efficiency of an antenna is \(66\%\). If the power input to the antenna is \(10\text{ W}\) what is the power radiated by the antenna in \(\text{dBm}\)?
8. An antenna with an input of \(1\text{ W}\) operates in free space and has an antenna gain of \(12\text{ dBi}\). What is the maximum power density at \(100\text{ m}\) from the antenna?
9. A transmitter has an antenna with an antenna gain of \(10\text{ dBi}\), the resistive losses of the antenna are \(50\%\), and the power input to the antenna is \(1\text{ W}\). What is the EIRP in watts?
10. A transmitter has an antenna with an antenna gain of \(20\text{ dBi}\), the resistive losses of the antenna are \(50\%\), and the power input to the antenna is \(100\text{ mW}\). What is the EIRP in watts?
11. An antenna with an antenna gain of \(8\text{ dBi}\) radiates \(6.67\text{ W}\). What is the EIRP in watts? Assume that the antenna is \(100\%\) efficient.
12. An antenna has an antenna gain of \(10\text{ dBi}\) and a \(40\text{ W}\) input signal. What is the EIRP in watts?
13. An antenna with \(5\text{ W}\) of input power has an antenna gain of \(20\text{ dBi}\) and an antenna efficiency of \(25\%\) and all of the loss is due to resistive losses in the antenna. [Parallels Example 4.5.2]
    1. How much power in \(\text{dBm}\) is lost as heat in the antenna?
    2. How much power in \(\text{dBm}\) is radiated by the antenna?
    3. What is the EIRP in \(\text{dBW}\)?
14. An antenna with an efficiency of \(50\%\) has an antenna gain of \(12\text{ dBi}\) and radiates \(100\text{ W}\). What is the EIRP in watts?
15. An antenna with an efficiency of \(75\%\) and an antenna gain of \(10\text{ dBi}\). If the power input to the antenna is \(100\text{ W}\),
    1. what is the total power in \(\text{dBm}\) radiated by the antenna?
    2. what is the EIRP in \(\text{dBm}\)?
16. On a resonant antenna a large current is established by creating a standing wave. The current peaking that thus results establishes a strong electric field (and hence magnetic field) that radiates away from the antenna. A typical dipole loses \(15\%\) of the power input to it as resistive (\(I^{2}R\)) losses and has an antenna gain of \(10\text{ dBi}\) measured at \(50\text{ m}\). Consider a base station dipole antenna that has \(100\text{ W}\) input to it. Also consider that the transmitted power density falls off with distance \(d\) as \(1/d^{3}\). Hint, calculate the power density at \(50\text{ m}\). [Parallels Example 4.5.1]
    1. What is the input power in \(\text{dBm}\)?
    2. What is the power transmitted in \(\text{dBm}\)?
    3. What is the power density at \(1\text{ km}\)? Express your answer as \(\text{W/m}^{2}\).
    4. What is the power captured by a receive antenna (at \(1\text{ km}\)) that has an effective antenna aperture of \(6\text{ cm}^{2}\)? Express your answer in first \(\text{dBm}\) and then watts.
    5. If the background noise level captured by the antenna is \(1\text{ pW}\), what is the SNR in decibels? Ignore interference that comes from other transmitters.
17. A communication system operating at \(2.5\text{ GHz}\) includes a transmit antenna with an antenna gain of \(12\text{ dBi}\) and a receive antenna with an effective aperture area of \(20\text{ cm}^{2}\). The distance between the two antennas is \(100\text{ m}\).
    1. What is the antenna gain of the receive antenna?
    2. If the input to the transmit antenna is \(1\text{ W}\), what is the power density at the receive antenna if the power falls off as \(1/d^{2}\), where \(d\) is the distance from the transmit antenna?
    3. Thus what is the power delivered at the output of the receive antenna?
18. Consider a point-to-point communication system. Parabolic antennas are mounted high on a mast so that ground effects do not exist, thus power falls off as \(1/d^{2}\). The gain of the transmit antenna is \(20\text{ dBi}\) and the gain of the receive antenna is \(15\text{ dBi}\). The distance between the antennas is \(10\text{ km}\). The effective area of the receive antenna is \(3\text{ cm}^{2}\). If the power input to the transmit antenna is \(600\text{ mW}\), what is the power delivered at the output of the receive antenna?
19. Consider a \(28\text{ GHz}\) point-to-point communication system. Parabolic antennas are mounted high on a mast so that ground effects do not exist, thus power falls off as \(1/d^{2}\). The gain of the transmit antenna is \(20\text{ dBi}\) and the gain of the receive antenna is \(15\text{ dBi}\). The distance between the antennas is \(10\text{ km}\). If the power output from the receive antenna is \(10\text{ pW}\), what is the power input to the transmit antenna?
20. An antenna has an effective aperture area of \(20\text{ cm}^{2}\). What is the antenna gain of the antenna at \(2.5\text{ GHz}\)?
21. An antenna operating at \(28\text{ GHz}\) has an antenna gain of \(50\text{ dBi}\). What is the effective aperture area of the antenna?
22. A \(15\text{ GHz}\) receive antenna has an antenna gain of \(20\text{ dBi}\). If the power density at the receive antenna is \(1\text{ nW/cm}^{2}\), what is the power at the output of the antenna? [Parallels Example 4.6.3]
23. A microstrip patch antenna operating at \(2\text{ GHz}\) has an efficiency of \(66\%\) and an antenna gain of \(8\text{ dBi}\). The power input to the antenna is \(10\text{ W}\).
    1. What is the power, in \(\text{dBm}\), radiated by the antenna?
    2. What is the equivalent isotropic radiated power (EIRP) in watts?
    3. What is the power density, in \(\mu\text{W/m}^{2}\), at \(1\text{ km}\) if ground effects are ignored?
    4. Because of multipath effects, the power density drops off as \(1/d^{4}\), where \(d\) is distance. What is the power density, in \(\text{nW/m}^{2}\), at \(1\text{ km}\) if the power density is \(100\text{ mW/m}^{2}\) at \(10\text{ m}\) from the transmit antenna?
24. A communication system operating at \(10\text{ GHz}\) uses a microstrip patch antenna as a transmit antenna and a dipole antenna as a receive antenna. The transmit antenna is directly connected to the transmitter and the output power of the transmitter is \(30\text{ W}\). The transmit antenna has an antenna gain of \(9\text{ dBi}\) and an antenna efficiency of \(60\%\). The receive antenna has an antenna gain of \(2\text{ dBi}\) and a radiation efficiency of \(80\%\). The receive antenna is connected to a receiver by a \(10\text{ m}\) long cable with a loss of \(0.1\text{ dB/m}\). The link between the transmit and receive antenna is sufficiently elevated that ground effects and multipath effects are insignificant.
    1. What is the output power of the transmitter in \(\text{dBm}\)?
    2. What is the EIRP in \(\text{dBm}\)?
    3. The transmitted power will drop off as \(1/d^{n}\) (\(d\) is distance). What is \(n\)?
    4. What is the peak power density in \(\mu\text{W/m}^{2}\) at \(1\text{ km}\)?
    5. What is the effective aperture size of the receive antenna in \(\text{m}^{2}\)?
    6. If the radiated power density at the receive antenna is \(\:\mu\text{W/m}^{2}\), what is the signal power at the output of the receive antenna in \(\text{dBm}\)?
    7. What is the total cable loss in \(\text{dB}\)?
    8. What is the power presented to the receiver in \(\text{dBm}\)?
25. A communication system operating at \(10\text{ GHz}\) uses a microstrip patch antenna as a transmit antenna and a dipole antenna as a receive antenna. The transmit antenna is connected to the transmitter by a \(20\text{ m}\) long cable with a loss of \(0.2\text{ dB/m}\) and the output power of the transmitter is \(30\text{ W}\). The transmit antenna has an antenna gain of \(9\text{ dBi}\) and an antenna efficiency of \(60\%\). The link between the transmit and receive antenna is sufficiently elevated that ground effects and multipath effects are insignificant.
    1. What is the output power of the transmitter in \(\text{dBm}\)?
    2. What is the cable loss between the transmitter and the antenna?
    3. What is the total power radiated by the transmit antenna in \(\text{dBm}\)?
    4. What is the power lost in the antenna as resistive losses and spurious radiation? Express your answer in \(\text{dBm}\).
    5. What is the EIRP of the transmitter in \(\text{dBm}\)?
    6. The transmitted power will drop off as \(1/d^{n}\) (\(d\) is distance). What is \(n\)?
    7. What is the peak power density in \(\mu\text{W/m}^{2}\) at \(1\text{ km}\)?
26. Stacked dipole antennas are often found at the top of cellphone masts, particularly for large cells and operating frequencies below \(1\text{ GHz}\). These antennas have an efficiency that is close to \(90\%\). Consider an antenna that has \(40\text{ W}\) of input power, an antenna gain of \(10\text{ dBi}\), and transmits a signal at \(900\text{ MHz}\).
    1. What is the EIRP in watts?
    2. If the power density drops as \(1/d^{3}\), where \(d\) is the distance from the transmit tower, what is the power density at \(1\text{ km}\) if the power density is \(100\text{ mW/m}^{2}\) at \(10\text{ m}\)?
27. Consider an \(18\text{ GHz}\) point-to-point communication system. Parabolic antennas are mounted on masts and the LOS between the antennas is just above the tree line. As a result, power falls off as \(1/d^{3}\), where \(d\) is the distance between the antennas. The gain of the transmit antenna is \(20\text{ dBi}\) and the gain of the receive antenna is \(15\text{ dBi}\). The antennas are aligned so that they are in each other’s main beam. The distance between the antennas is \(1\text{ km}\). The transmit antenna is driven by a power amplifier with an output power of \(100\text{ W}\). The amplifier drives a coaxial cable that is connected between the amplifier and the transmit antenna. The cable loses \(75\%\) of its power due to resistive losses. On the receive side, the receive antenna is directly connected to a masthead amplifier with a gain of \(10\text{ dB}\) and then a short cable with a loss of \(3\text{ dB}\) before entering the receive base station.
    1. Draw the signal path.
    2. What is the loss and gain of the transmitter coaxial cable in decibels?
    3. What percentage of the power input to the receive coaxial cable is lost in the receive cable?
    4. Express the power of the transmit amplifier in \(\text{dBW}\) and \(\text{dBm}\).
    5. What is the propagation loss in decibels?
    6. Determine the total power in watts delivered to the receive base station.
28. Consider a point-to-point communication system. Parabolic antennas are mounted high on a mast so that ground effects are minimal. Thus power density falls off as \(1/d^{2.3}\), where \(d\) is the distance from the transmitter. The gain of the transmit antenna is \(15\text{ dBi}\) and the gain of the receive antenna is \(12\text{ dBi}\). These antenna gains are normalized to a distance of \(1\text{ m}\). The distance between the antennas is \(15\text{ km}\). The output power of the receive antenna must be \(1\text{ pW}\). The RF frequency is \(2\text{ GHz}\); treat the antennas as lossless.
    1. What is the received power in \(\text{dBm}\)?
    2. What is the path loss in decibels?
    3. What is the link loss in decibels?
    4. Using the link loss, calculate the input power, \(P_{T}\), of the transmitter. Express the answer in \(\text{dBm}\).
    5. What is the aperture area of the receiver in square meters?
    6. Determine the radiated power density at the receiver in terms of the transmitter input power. That is, if \(P_{T}\) is the power input to the transmit antenna, determine the power density, \(P_{D}\), at the receive antenna where \(P_{D} = xP_{T}\). What is \(x\) in units of \(\text{m}^{−2}\)?
    7. Using the power density calculation and the aperture area, calculate \(P_{T}\) in watts.
    8. What is \(P_{T}\) in \(\text{dBm}\)? This should be the same as the answer you calculated in (d).
    9. What is the total power radiated by the transmit antenna in \(\text{dBm}\)?
29. Two identical antennas are used in a point-to-point communication system, each having a gain of \(50\text{ dBi}\). The system has an operating frequency of \(28\text{ GHz}\) and the antennas are at the top of masts \(100\text{ m}\) tall. The RF link between the antennas consists only of the direct line-of-sight path.
    1. What is the effective aperture area of each antenna?
    2. How does the power density of the propagating signal rolloff with distance.
    3. If the separation of the transmit and receive antennas is \(10\text{ km}\), what is the path loss in decibels?
    4. If the separation of the transmit and receive antennas is \(10\text{ km}\), what is the link loss in decibels?
30. A transmitter and receiver operating at \(2\text{ GHz}\) are at the same level, but the direct path between them is blocked by a building and the signal must diffract over the building for a communication link to be established. This is a classic knife-edge diffraction situation. The transmit and receive antennas are each separated from the building by \(4\text{ km}\) and the building is \(20\text{ m}\) higher than the antennas (which are at the same height). Consider that the building is very thin. It has been found that the path loss can be determined by considering loss due to free-space propagation and loss due to diffraction over the knife edge.
    1. What is the additional attenuation (in decibels) due to diffraction?
    2. If the operating frequency is \(100\text{ MHz}\), what is the attenuation (in decibels) due to diffraction?
    3. If the operating frequency is \(10\text{ GHz}\), what is the attenuation (in decibels) due to diffraction?
31. A hill is \(1\text{ km}\) from a transmit antenna and \(2\text{ km}\) from a receive antenna. The receive and transmit antennas are at the same height and the hill is \(20\text{ m}\) above the height of the antennas. What is the additional loss caused by diffraction over the top of the hill? Treat the hill as a knife-edge and the operating frequency is \(1\text{ GHz}\).
32. A \(1\text{ GHz}\) point-to-point link has two major transmission paths. One is a LOS path and the other includes reflection from the ground so that the power density of the transmitted signal rollsoff as \(1/d^{2.5}\) where \(d\) is the distance from the transmit antenna. At \(10\text{ m}\) the power density from the transmit antenna is \(100\text{ mW/m}^{2}\).
    1. What is the power density at \(1\text{ km}\).
    2. If the receive antenna has an antenna gain of \(30\text{ dBi}\), what is the effective aperture area of the receive antenna?
    3. What is the power of the signal at the output of the receive antenna?
33. Two identical antennas are used in a point-to-point communication system, each having a gain of \(30\text{ dBi}\). The system has an operating frequency of \(14\text{ GHz}\) and the antennas are at the top of masts \(100\text{ m}\) tall. The RF link between the antennas consists only of the direct LOS path.
    1. What is the effective aperture area of each antenna?
    2. How does the power density of the propagating signal rolloff with distance?
    3. If the separation of the transmit and receive antennas is \(10\text{ km}\), what is the path loss? Ignore atmospheric loss.
34. The three main cellular communication bands are centered around \(450\text{ MHz},\: 900\text{ MHz},\) and \(2\text{ GHz}\). Compare these three bands in terms of multipath effects, diffraction around buildings, object (such as a wall) penetration, scattering from trees and parts of trees, and ability to follow the curvature of hills. Complete the table below with the relative attributes: high, medium, and low.

    Characteristic	\(450\text{ MHz}\)	\(900\text{ MHz}\)	\(2\text{ GHz}\)
    Multipath
    Scattering
    Penetration
    Following curvature
    Range
    Antenna size
    Atmospheric loss

    Table \(\PageIndex{1}\)

35. Describe the difference in multipath effects in a central city area compared to multipath effects in a desert. Your description should be approximately \(4\) lines long and not use a diagram.
36. Wireless LAN systems can operate at \(2.4\text{ GHz},\: 5.6\text{ GHz},\: 40\text{ GHz}\) and \(60\text{ GHz}\). Contrast with explanation the performance of these schemes inside a building in terms of range.
37. At \(60\text{ GHz}\) the atmosphere strongly attenuates a signal. Discuss the origin of this and indicate an advantage and a disadvantage.
38. Short answer questions. Each part requires a short paragraph of about five lines and a figure, where appropriate, to illustrate your understanding.
    1. Cellular communications systems use two frequency bands to communicate between the basestation and the mobile unit. The bands are generally separated by \(50\text{ MHz}\) or so. Which band (higher or lower) is used for the downlink from the basestation to the mobile unit and what are the reasons behind this choice?
    2. Describe at least two types of interference in a cellular system from the perspective of a mobile handset.
39. The three main cellular communication bands are centered around \(450\text{ MHz},\: 900\text{ MHz},\) and \(2\text{ GHz}\). Compare these three bands in terms of multipath effects, diffraction around buildings, object (such as a wall) penetration, scattering from trees and parts of trees, and the ability to follow the curvature of hills. Use a table and indicate the relative attributes: high, medium, and low. WAS 10(C)
40. Describe Rayleigh fading in approximately \(4\) lines and without using a diagram.
41. In several sentences and using a diagram describe Rayleigh fading and the impact it has on radio communications.
42. A transmit antenna and a receive antenna are separated by \(1\text{ km}\) and operate at \(1\text{ GHz}\). What is the radius of the first Fresnel zone at \(0.5\text{ km}\) from each antenna? [Parallels Example 4.6.4]
43. A transmit antenna and a receive antenna are separated by \(40\text{ km}\) and operate at \(10\text{ GHz}\). [Parallels Example 4.6.4]
    1. What is the radius of the first Fresnel zone at the midpoint between the antennas?
    2. What is the radius of the second Fresnel zone?
    3. To ensure LOS propagation, what should the clearance be from the direct line between the antennas and obstructions such as hills?
44. A transmitter and receiver operate at \(100\text{ MHz}\), are at the same level, and are separated by \(4\text{ km}\). The signal must diffract over a building half way between the antennas that is \(20\text{ m}\) higher than the direct path between the antennas. What is the attenuation (in decibels) due to diffraction?
45. A transmitter and receiver operate at \(10\text{ GHz}\), are at the same level, and are \(4\text{ km}\) apart. The signal must diffract over a building that is half way between the antennas and is \(20\text{ m}\) higher than the line between the antennas. What is the attenuation (in \(\text{dB}\)) due to diffraction?
46. The path from a transmit antenna to a receive antenna is elevated so that ground and multipath effects are insignificant. The power radiated by the transmit antenna drop off as \(1/d^{n}\) where \(d\) is distance, what is \(n\)?
47. A communication system has a power density roll-off of \(1/d^{2.5}\) between a transmit antenna and a mobile receive antenna which are separated by \(10\text{ km}\). At \(10\text{ m}\) from the transmit antenna, the power density is \(10\text{ W/m}^{2}\). What is the power density at the receive antenna? [Parallels Example 4.6.1]
48. A \(900\text{ MHz}\) communication system uses a transmit antenna with an antenna gain \(G_{T}\) of \(3\text{ dB}\) and a receive antenna with an antenna gain \(G_{R}\) of \(0\text{ dB}\). If the distance between the antennas is \(200\text{ m}\), what is the link loss from the input to the transmit antenna and the output of the receive antenna if the power density reduces as \(1/d^{2.5}\)? [Parallels Example 4.6.2]
49. A transmitter has a power density of \(100\text{ mW/m}^{2}\) at a distance of \(1\text{ m}\) from the transmitter. The power density falls off as \(33\text{ dB}\) per decade of distance. At what distance from the transmit antenna will the power density reach \(1\:\mu\text{W}\cdot\text{m}^{-2}\)? [Parallels Example 4.6.3]
50. Describe at least two types of interference in a cellular system from the perspective of a mobile handset.
51. In a cellular system, a signal is intentionally transmitted from a base station nominally located in the center of a cell to a mobile unit in the same cell. However, nearby transmitters using the same channel cause interference. In Figure 4.8.4, a mobile unit is located at the edge of a cell and uses frequency channel A. Many nearby transmitters also operate using channel A and the six nearest transmitters can be considered as causing significant interference. Consider that the mobile unit is a distance \(r\) from its cell’s transmitter along the line connecting two channel A base stations, that the transmitters all operate at the same power level, and that the distance between base stations operating using channel A is \(3r\). This three-cell cluster operates in a suburban area and the power density drops off with distance \(d\) as \(1/d^{3.5}\) due to multipath effects. What is the SIR at the mobile unit? Express your answer in decibels. [Parallels Example 4.8.1]
52. A cellular system uses a three-cell cluster.
    1. Treating cells as equal sized hexagons with towers in the center of each cell, draw the cell map including all cells within \(3\) cell diameters of the main channel. Label the main cell and other cells using the same frequencies as A.
    2. Consider a mobile unit at the edge of a cell transmitting the intended signal from the tower at the center of that cell. Identify the interfering towers.
    3. If ground effects and multipath effects are negligible, what is the power roll-off factor if the distance between a tower and the mobile unit is \(d\)? That is, what is n if power falls off as \(1/d^{n}\)?
    4. If trisector antennas are used, identify the interfering cells and approximately determine the improvement in SIR compared to using a nonsectorized antenna? You do not need to do detailed calculations.
53. Describe trisector antennas in \(4\) lines and without using a diagram.

4.12.1 Exercises By Section

\(†\)challenging, \(‡\)very challenging

\(§14.3 1†\)

\(§14.5 2†, 3†, 4‡, 5, 6, 7†, 8†, 9†, 10, 11, 12, 13, 14, 15, 16‡, 17, 18, 19, 22 \)

\(§14.6 23‡, 24‡, 25‡, 26‡, 27‡, 28‡, 29†, 30†, 31†, 32‡, 33†, 34‡, 35†, 36, 37, 38†, 39, 40, 41, 42†, 43, 44, 45, 46, 47, 48, 49 \)

\(§14.8 50†, 51‡, 52‡, 53†\)

4.12.2 Answers to Selected Exercises

2. (e) \(53.23\text{ dBm}\)

17. \(0.251\:\mu\text{W}\)
18. \(14.3\text{ pW}\)

23. (b) \(63.1\text{ W}\)

25. (e) \(49.77\text{ dBm}\)

27. (f) \(708\text{ pW}\)
28. \(107.65\text{ dB}\)

32. \(7.16\text{ m}^{2}\)

42. \(8.66\text{ m}\)

51. \(7.33\text{ dB}\)