5.5: Spectrum Efficiency

The concept of spectral efficiency is important in contrasting digital radio systems. Spectral efficiency has its origins in Shannon’s theorem, which expresses the information-carrying capacity of a channel as [16, 17, 18]

\[\label{eq:1}\hat{C}=B_{c}\log_{2}(1+\text{SNR}) \]

where \(\hat{C}\) is the capacity in units of bits per second (\(\text{bit/s}\)), \(B_{c}\) is the channel bandwidth in hertz, and SNR is the signal-to-noise ratio. \(N\) is assumed to be Gaussian noise, so interference that can be approximated as Gaussian can be incorporated by adding the noise and interference powers, and then it is more appropriate to use the SIR. Thus Equation \(\eqref{eq:1}\) becomes

\[\label{eq:2}\hat{C}=B_{c}\log_{2}[1+S/(N+I)]=B_{c}\log_{2}(1+\text{SIR}) \]

Shannon’s theorem is widely accepted as the upper limit on the information-carrying capacity of a channel. So the stronger the signal, or the lower the interfering signal, the greater a channel’s information-carrying capacity. Indeed, if there is no noise and no interference, the information-carrying capacity is infinite. Shannon’s capacity formula indicates that increasing the interference level (lower SIR) has a more weakened effect on the decrease in capacity than may initially be expected; that is, doubling the interference level does not halve \(\hat{C}\). This is the conceptual insight that supports the use of closely packed cells and frequency reuse, as the resulting increase in interference, and its moderated effect on capacity, is offset by having more cells and supporting more users.

Shannon’s carrying capacity limit has not been reached, but today’s radio systems are very close. Current systems operate with SNRs only a few decibels away from the limit [16]. Different modulation and radio schemes come closer to the limit, and two quantities will be introduced here to describe the performance of different schemes. From the capacity formula, a useful metric for the performance of modulation schemes can be defined. This is the modulation efficiency (also referred to as the channel efficiency, channel spectrum efficiency, and channel spectral efficiency),

\[\label{eq:3}\eta_{c}=R_{c}/B_{c} \]

where \(R_{c}\) (in \(\text{bit/s}\)) is the bit rate transmitted on the channel, so \(\eta_{c}\) has the units of \(\text{bit/s/Hz}\). The unit is dimensionless, as hertz has the units of \(\text{s}^{−1}\).

In a cellular system, the number of cells in a cluster must be incorporated to obtain a system metric [19]. The available channels are divided among the cells in a cluster, and a channel in one cell appears as interference to a corresponding cell in another cluster. Thus the SIR is increased and the capacity of the channel drops. System throughput increases, however, because of closely packed cells. So the system throughput is a function of the frequency reuse pattern. The appropriate system-level metric is the radio spectrum efficiency, \(\eta_{r}\), which incorporates the number of cells, \(K\), in a cluster:

\[\label{eq:4}\eta_{r}=\frac{R_{b}}{B_{c}K}=\frac{\eta_{c}}{K}\frac{R_{b}}{R_{c}} \]

where \(R_{b}\) is the bit rate of useful information \(R_{c}\), (\(R_{c}\) is higher than \(R_{b}\) because of coding). Coding is used to enable error correction, assist in identifying the start and end of a packet, and also to provide orthogonality of users in some systems that overlap users as with CDMA. The units of \(\eta_{r}\) are \(\text{bit/s/Hz/cell}\). The decrease in channel capacity resulting from the increased SIR associated with fewer cells in a cluster (i.e., lower \(K\)) is more than offset by the increased system throughput.

So there are two definitions of spectral efficiency: the channel spectrum efficiency (also known as the modulation efficiency), \(\eta_{c}\), which characterizes the efficiency of a modulation scheme, and the radio spectrum efficiency, \(\eta_{r}\), which incorporates the added interference that comes from frequency reuse. Commonly both measures of efficiency are referred to as spectral efficiency, and then only the units identify which is being referred to.

One may well ask why efficiency is not expressed as a ratio of actual bit rate to Shannon’s limit for a given set of conditions. There are several reasons:

1. The historical use of bits per hertz to characterize a modulation scheme was used long before cellular systems came about.
2. Shannon’s capacity limit is so high that back in the 1950s people would have been talking about extremely low efficiencies if performance was referred to the capacity limit.
3. Only additive white noise is considered, but this does not capture all types of interference, which can be multiplicative or partially correlated with the signal. Shannon’s limit is not really a theoretical limit, there is no proof. In the digital communications world, much has been published about how close Shannon’s capacity limit can be approached. In a direct LOS system, such as a point-to-point microwave link, the limit is now approached within a few percent. In MIMO systems, (see Section 5.10.5) the limit has been exceeded, prompting a redefinition of the limit when multiple transmit and receive antennas are used.

Example \(\PageIndex{1}\): Modulation Efficiency

A radio uses a modulation scheme based on 16-QAM but the four constellation points corresponding to the largest signal are not used. Consequently the distortion that would occur in RF amplifiers is reduced. Even though there are \(4\text{ bits}\) of information per symbol for the symbols that are actually used, not every possible combination of the bits is used. Ignoring error correction coding all of the bits modulated are information bits.

Solution

1. Draw the constellation diagram.

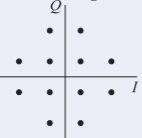
Figure \(\PageIndex{1}\)

2. How many symbols are there?
   \(12\)
3. On average, how many bits of information are transmitted per symbol?
   It takes \(8\) symbols to transmit \(3\text{ bits}\) of information and \(16\) symbols to transmit \(4\text{ bits}\). With 12QAM \(8\) symbols are sent in the first clock tick interval and \(4\) symbols are borrowed from the second clock tick interval to provide \(16\) symbols combined and hence \(4\text{ bits}\) of information. There are \(8\) symbols left over in the second clock tick interval and these can be used to send \(3\text{ bits}\). Thus over two clock tick intervals \(7\text{ bits}\) of information are sent. Thus in one clock tick interval \(3.5\text{ bits}\) are transmitted. So the number of bits of information sent by each symbol is \(3.5\text{ bits}\).
4. What is the maximum possible modulation efficiency, \(\eta_{c}\), in \(\text{bit/s/Hz}\)?
   Ideally \(\eta_{c}\) is equal to the number of bits per symbol. However not all of the symbol transitions are of equal length and the bandwidth must be high enough to allow the longer transitions to take place in the same amount of time as the short transitions. However the maximum possible modulation efficiency is \(3.5\text{ bit/s/Hz}\).