3.7: Case Study- Distributed Biasing of Differential Amplifiers

In this case study a broadband distributed balun-like section is presented as an alternative to inductor-biasing of a pseudo-differential amplifier (PDA). The distributed biasing circuit discriminates between differential-and common-mode signals, resulting in rejection of common-mode signals. A PDA is shown in Figure \(\PageIndex{1}\), where the inductors present high RF impedances to the transistors while providing low-impedance paths for bias currents. However, inductive biasing of pseudo-differential circuits presents the same environment to common- and differential-mode signals so that the CMRR is \(1\).

Differential amplifiers have large differential gain, \(A_{d}\). At the same time it is desirable to minimize the common-mode gain, \(A_{c}\), as the resulting high CMRR provides immunity to substrate-induced noise. Considering that each transistor has transconductance, \(g_{m}\), and that even- and odd-mode impedances, \(Z_{\text{EVEN}}\) and \(Z_{\text{ODD}}\), are presented to the drains of the transistors, then the gains are approximately

\[\label{eq:1}A_{d}=g_{m}Z_{\text{ODD}}\quad\text{and}\quad A_{c}=g_{m}Z_{\text{EVEN}} \]

and so

\[\label{eq:2}\text{CMRR}=A_{d}/A_{c}=Z_{\text{ODD}}/Z_{\text{EVEN}} \]

The desired amplifier characteristics are thus obtained by synthesizing the even- and odd-mode impedances.

First consider the inductively biased circuit in Figure \(\PageIndex{1}\). Modal analysis of the inductor biasing circuit results in the circuit model shown in Figure \(\PageIndex{2}\), from which the total even-mode impedance is

\[\label{eq:3}Z_{\text{EVEN}}(s)=(s_{L}+R_{DD}/2)//R_{L} \]

where \(//\) indicates a parallel connection, and the total odd-mode impedance is

\[\label{eq:4}Z_{\text{ODD}}(s)=sL//R_{L} \]

Since \(R_{DD}\) is usually negligible and \(L\) is a bias or choke inductor so that \(sL\) is very large, \(Z_{\text{ODD}}\approx R_{D}\approx Z_{\text{EVEN}}\) and so the CMRR is \(1\). However, a coupled-line network can provide different model impedances.

Now consider the Marchand balun-like structure in Figure \(\PageIndex{3}\) that replaces the drain bias circuit in Figure \(\PageIndex{1}\). The Marchand Balun structure

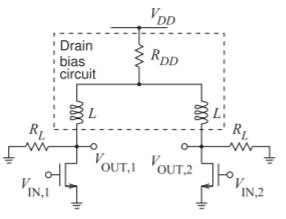
Figure \(\PageIndex{1}\): A PDA amplifier with bias inductors, \(L\), at the drains, parasitic supply resistance, \(R_{DD}\), and single-ended load impedance, \(R_{L}\). \(L\) is also known as a choke inductor chosen so that its impedance is very large at the maximum operating frequency, i.e. \(|sL| ≫ R_{L}\).

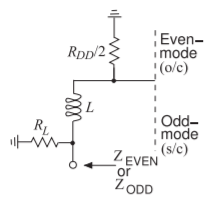
Figure \(\PageIndex{2}\): Modal subcircuits of the inductor-based biasing circuit of Figure \(\PageIndex{1}\), including single-ended load resistance \(R_{L}\).

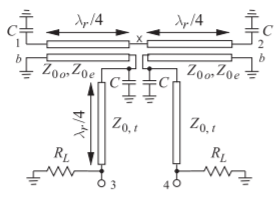
Figure \(\PageIndex{3}\): Marchand balun-like biasing circuit with single-ended load resistance \(R_{L}\). External DC bias is applied at Ports \(b\) using decoupling capacitors to ensure RF ground.

presents different impedances for common- and differential-mode signals. The synthesis of this biasing circuit is described in [8, 9] and follows a procedure similar to that for filter design. So high CMRR performance is the result of presenting different even- and odd-mode impedances to the active devices. The final results of the design are shown in Figure 3.8.1, first for inductive-biasing of the PDA and then for the coupled-line balun-like biasing circuit.