Skip to main content
Engineering LibreTexts

3.11: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    46033

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Consider a \(Z_{0} = 50\:\Omega\) transmission line of length \(\lambda /10\) at \(30\text{ GHz}\).
      1. Calculate the \(ABCD\) parameters of the transmission line at \(30\text{ GHz}\)?
      2. With the transmission line shunted by \(0.05\text{ pF}\) capacitors at each end, calculate the \(ABCD\) parameters of the augmented transmission line.
      3. At \(30\text{ GHz}\) the augmented transmission line is equivalent to a single transmission line with characteristic impedance \(Z_{01}\) and length \(\ell_{1}\). What is \(\ell_{1}\) in terms of wavelengths?
      4. What is \(Z_{01}\)?
    2. A four-stage distributed FET amplifier as shown in Figure 3.2.1 has \(R_{S} = R_{L} = 50\:\Omega\). If the capacitive and resistive loading of the transistors are ignored, what are the optimum values of \(R_{1}\) and \(R_{2}\)? Provide your reasoning.
    3. The four-stage distributed FET amplifier shown in Figure 3.2.1 has \(R_{S} = 80\:\Omega\) and \(R_{L} = 25\:\Omega\). If the capacitive and resistive loading of the transistors are ignored, what are the optimum values of \(R_{1}\) and \(R_{2}\)? Provide your reasoning.
    4. The input matching network of the wideband amplifier considered in Section 3.5 is shown in Figure 3.5.9(b). (Note that Port 2 of the input network is connected to the transistor.) Typically the complex conjugate of \(S_{22}\) of the input network would match the input reflection coefficient, \(\Gamma_{\text{in}}\), of the transistor. Put your answers in magnitude-angle form.
      1. Draw the input matching network showing where \(S_{22}\) is determined. Also draw the transistor terminated by the output matching network and indicate where \(\Gamma_{\text{in}}\) is calculated.
      2. Use a microwave simulator to calculate the \(S_{22}\) of the input matching network at \(8, 9, ..., 12\text{ GHz}\).
      3. Determine \(S_{22}^{\ast}\) of the input matching network at \(8, 9, ..., 12\text{ GHz}\).
      4. Determine \(S_{11}\) of the transistor at \(8, 9, ..., 12\text{ GHz}\).
      5. Determine \(\Gamma_{\text{in}}\) of the transistor (terminated in the output matching network) at \(8, 9, ..., 12\text{ GHz}\).
      6. On a Smith chart plot \(S_{22}^{\ast}\) of the input network, \(S_{11}\) of the transistor, and \(\Gamma_{\text{in}}\) of the transistor.
      7. Describe the input matching network condition for maximum power transfer used in narrowband amplifier design.
      8. Discuss the mismatch of \(\Gamma_{\text{in}}\) of the transistor and \(S_{22}^{\ast}\) of the input matching network. Describe the effect that this has on the broadband response of the amplifier.
    5. The output matching network of the wideband amplifier considered in Section 3.5 is shown in Figure 3.5.10(b). (Note that Port 2 of the input network is connected to the transistor.) Typically the complex conjugate of \(S_{22}\) of the output network would match the input reflection coefficient, \(\Gamma_{\text{out}}\), of the transistor. Put your answers in magnitude-angle form.
      1. Draw the output matching network showing where \(S_{22}\) is determined. Also draw the transistor terminated by the input matching network and indicate where \(\Gamma_{\text{out}}\) is calculated.
      2. Use a microwave simulator to calculate the \(S_{22}\) of the output matching network at \(8, 9, ..., 12\text{ GHz}\).
      3. Determine \(S_{22}^{\ast}\) of the output matching network at \(8, 9, ..., 12\text{ GHz}\).
      4. Determine \(S_{22}\) of the transistor at \(8, 9, ..., 12\text{ GHz}\).
      5. Determine \(\Gamma_{\text{out}}\) of the transistor (terminated in the output matching network) at \(8, 9, ..., 12\text{ GHz}\).
      6. On a Smith chart plot \(S_{22}^{\ast}\) of the output network, \(S_{22}\) of the transistor, and \(\Gamma_{\text{out}}\) of the transistor.
      7. Describe the output matching network condition for maximum power transfer used in narrowband amplifier design.
      8. Discuss the mismatch of \(\Gamma_{\text{out}}\) of the transistor and \(S_{22}^{\ast}\) of the output matching network. Describe the effect that this has on the broadband response of the amplifier. You will want to consider the \(S_{21}\) of the transistor.
    6. Plot the \(50\:\Omega\:S_{11}\) and \(S_{22}\) parameters from \(8\text{ GHz}\) to \(12\text{ GHz}\) of the wideband amplifier considered in Section 3.5. It will be seen that the amplifier is not matched across the band. Discuss the reason why there is a mismatch even though the gain and noise figure of the amplifier, shown in Figure 3.6.1, are relatively flat from from \(8\text{ GHz}\) to \(12\text{ GHz}\). Note that Port 1 is the input port of the amplifier and Port 2 is the output Port.
    7. The output of a transistor is modeled as the shunt connection of a current source, a \(20\:\Omega\) resistor, a \(0.35\text{ pF}\) capacitor, and a \(0.7\text{ nH}\) inductor.
      1. What is the admittance of the transistor output at \(8,\: 10,\) and \(12\text{ GHz}\)?
      2. How does the susceptance vary with frequency?
      3. What is the shunt reactive element required to resonate the output admittance of the transistor at \(8,\: 10,\) and \(12\text{ GHz}\)?
      4. What are the equivalent inductances required to resonate the output admittance of the transistor at \(8,\: 10,\) and \(12\text{ GHz}\)?
      5. How does the inductance calculated in (d) vary with frequency?
      6. Describe a two-element circuit that has the characteristic identified in (e). (Note that this circuit would only be able to achieve the required characteristic over a smaller bandwidth than that required for a match from \(8\text{ GHz}\) to \(12\text{ GHz}\).)
    8. The output of a transistor is modeled as the shunt connection of a current source, a \(68\:\Omega\) resistor, a \(0.35\text{ pF}\) capacitor, and a \(0.7\text{ nH}\) inductor.
      1. What is the output admittance of the transistor at \(8,\: 10\) and \(12\text{ GHz}\)?
      2. How does the admittance vary with frequency?
      3. Design a lumped-element matching network with two elements to match the transistor output at \(10\text{ GHz}\) to a \(50\:\Omega\) source.
      4. Calculate the input admittance of the matching network, looking from the transistor, at \(8,\: 10,\) and \(12\text{ GHz}\).
      5. What is the input admittance of an ideal matching network, looking from the transistor, at \(8,\: 10,\) and \(12\text{ GHz}\)? Plot the actual and ideal admittance loci on a Smith chart using markers at \(8,\: 10,\) and \(12\text{ GHz}\) and indicating the direction of increasing frequency with arrows.
    9. Consider a transistor having the \(S\) parameters shown in Table 3.5.1 and Figure 3.5.2(a). Ignore feedback effects and consider that the reflection coefficient looking into the output of the transistor is \(S_{22}^{\ast}\).
      1. Draw and describe the two-port input matching network problem with Port 1 at the output of the transistor and a \(50\:\Omega\) termination at Port 2.
      2. What is the ideal \(S_{11}\) of the input matching two-port at \(8\text{ GHz}\)?
      3. What is the ideal \(S_{11}\) of the input matching two-port at \(10\text{ GHz}\)?
      4. What is the ideal \(S_{11}\) of the input matching two-port at \(12\text{ GHz}\)?
      5. Plot the locus from \(8\text{ GHz}\) to \(12\text{ GHz}\) of \(S_{11}\) of the input matching two-port on a Smith chart.
      6. Assume that the locus plotted in (e) from \(8\text{ GHz}\) to \(12\text{ GHz}\) can be realized using a lumped-element network. Comment on the difficulty of the design and the design approach.
    10. At \(10\text{ GHz}\) a capacitor, \(C_{1}\), has a reactance of \(−50\:\Omega\).
      1. What is the impedance of \(C_{1}\) at \(8,\: 10,\) and \(12\text{ GHz}\)?
      2. How does the impedance of \(C_{1}\) vary with frequency?
      3. What is the inductance required to resonate the capacitance at \(8,\: 10,\) and \(12\text{ GHz}\)?
      4. How does the inductance calculated in (b) vary with frequency?
    11. The input of a transistor is modeled as a \(20\:\Omega\) resistor in series with a \(0.3\text{ pF}\) capacitor.
      1. What is the impedance of the transistor input at \(8,\: 10,\) and \(12\text{ GHz}\)?
      2. How does the impedance vary with frequency?
      3. What is the series inductance required to resonate out the transistor capacitance at \(8,\: 10,\) and \(12\text{ GHz}\)?
      4. Comment on whether a wideband match of a resistive source to the input of a transistor can be achieved using a frequency-independent inductor.
    12. The input of a transistor is modeled as a \(20\:\Omega\) resistor in series with a \(0.3\text{ pF}\) capacitor. The transistor is part of an amplifier operating in a \(50\:\Omega\) system.
      1. Design a lumped-element matching network with two elements (inductors and/or capacitors) to match the transistor input at \(10\text{ GHz}\) to a \(50\:\Omega\) source.
      2. Calculate the return loss (looking into the matching network from the source) at \(8,\: 9,\: 10,\: 11,\) and \(12\text{ GHz}\).
      3. Calculate the fraction of the available input power, expressed in decibels, delivered to the transistor at \(8,\: 9,\: 10,\: 11,\) and \(12\text{ GHz}\) and indicate the direction of increasing frequency with arrows.
      4. Comment on the variation in amplifier gain solely due to mismatch at the transistor input.
    13. Consider the input of a transistor having the \(S\) parameters shown in Table 3.5.1 and Figure 3.5.2(a). Ignore feedback effects so that for the active device \(\Gamma_{\text{in}} = S_{11}\). Also an input matching network terminated in \(50\:\Omega\) at Port 1 and the active device at Port 2.
      1. What is the ideal \(50\:\Omega\: S_{22}\) of the input matching network (i.e., seen from the transistor input) at \(8\text{ GHz}\)?
      2. What is the ideal \(50\:\Omega\: S_{22}\) of the input matching network (i.e., seen from the transistor input) at \(10\text{ GHz}\)?
      3. What is the ideal \(50\:\Omega\: S_{22}\) of the input matching network (i.e., seen from the transistor input) at \(12\text{ GHz}\)?
    14. Consider matching the input of a transistor having the \(S\) parameters shown in Table 3.5.1 and Figure 3.5.2(a). Ignore feedback effects and consider that the input reflection coefficient of the transistor \(\Gamma_{\text{in}} = S_{11}\). Curve B in Figure 3.5.2(a) is the locus of the impedance looking into the matching network from the transistor. What two-element network has this locus? (One of the elements may be a resistor).
    15. Consider synthesizing a two-port matching network terminated in a \(50\:\Omega\) load and with an input reflection coefficient \(\Gamma_{1}\) shown as Curve B in Figure 3.5.2(a). Draw and describe the two-port matching network problem.
    16. Consider synthesizing a two-port matching network terminated in a \(50\:\Omega\) load and with an input reflection coefficient \(\Gamma_{1}\) shown as Curve B in Figure 3.5.2(a). Can a broadband match be obtained using a two-element matching network? Explain your answer in terms of rotations on a Smith chart.
    17. Consider the inductively biased differential Class A amplifier shown below. \(L_{D}\) is a choke inductor so \(|sL| ≫ R_{L}\).[Parallels Example 3.6.1.]

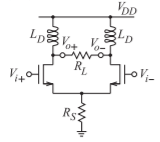
    clipboard_e0b16cc23b87cc46f89c153a49b4def29.png

    Figure \(\PageIndex{1}\)

    What is the CMRR when \(R_{S} = 20\text{ k}\Omega,\: R_{L} = 10\text{ k}\Omega\), the transistor transconductance, \(g_{m} = 50\text{ mS}\), and the drain-source resistance, \(r_{d}\) is \(100\text{ k}\Omega\)?

    1. Consider the inductively biased differential Class A amplifier shown below. The capacitors can be treated as RF short circuits. \(L_{D}\) is a choke inductor so \(|sL| ≫ R_{L}\). [Parallels Example 3.6.1]

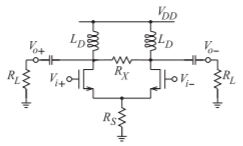
    clipboard_e841e986a4c2d89e0bd04f76e1d81cc56.png

    Figure \(\PageIndex{2}\)

    1. Derive a symbolic expression for the CMRR of the amplifier assuming that the drain-source resistance of the transistors, \(r_{0}\) or \(r_{d}\), is much greater than both \(R_{L}\) and \(R_{X}\), and so can be ignored.
    2. What is the CMRR when \(R_{S} = 10\text{ k}\Omega,\) \(R_{X} = 30\text{ k}\Omega\), \(R_{L} = 10\text{ k}\Omega\), and the transistor transconductance, \(g_{m}\) is \(10\text{ mS}\).
    1. Consider the inductively-biased differential Class A amplifier shown below. \(L_{D}\) is a choke inductor so \(|sL| ≫ R_{L}\). [Parallels Example 3.6.1]

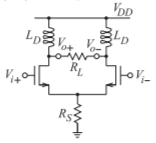
    clipboard_eca6ac9e2e0d4cf0bf034039d46aa76f4.png

    Figure \(\PageIndex{3}\)

    1. Derive a symbolic expression for the differential mode gain of the amplifier.
    2. Derive a symbolic expression for the CMRR of the amplifier.
    3. What is CMRR when \(R_{S} = 10\text{ k}\Omega\), \(R_{L} = 10\text{ k}\Omega\), the transistor transconductance, \(g_{m}\) is \(15\text{ mS}\), and the transistors’ drain-source resistance, \(r_{d}\), is \(100\text{ k}\Omega\)?
    1. A differential amplifier has a differential-mode gain of \(20\text{ dB}\) and a common-mode gain of \(−3\text{ dB}\).
      1. What is the the odd-mode gain?
      2. What is the the even-mode gain?
    2. Consider the differential amplifier below. [Parallels Example 3.6.1]

    clipboard_ef8e125a035829a39ed80be3ccb833235.png

    Figure \(\PageIndex{4}\)

    1. What is the differential load impedance?
    2. What is the odd-mode load impedance?
    3. What is the common-mode load impedance?
    4. What is the even-mode load impedance?
    1. Consider the differential amplifier below. [Parallels Example 3.6.1]

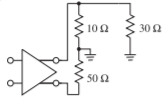
    clipboard_e8a57d4af4e87548e67e1e59909726e79.png

    Figure \(\PageIndex{5}\)

    1. What is the differential load impedance?
    2. What is the odd-mode load impedance?
    3. What is the common-mode load impedance?
    4. What is the even-mode load impedance?
    1. Consider the differential amplifier below. [Parallels Example 3.6.1]

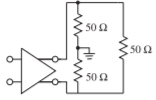
    clipboard_e38c7b30d2eeb1b0ecc7adb63a19ee05e.png

    Figure \(\PageIndex{6}\)

    1. What is the differential load impedance?
    2. What is the odd-mode load impedance?
    3. What is the common-mode load impedance?
    4. What is the even-mode load impedance?
    5. If the differential-mode gain of the amplifier is \(20\text{ dB}\) and the common-mode gain is \(2\text{ dB}\), what is the odd-mode gain?
    1. Consider the differential amplifier below. \(L_{D}\) is a choke inductor so \(|sL| ≫ R_{L}\). [Parallels Example 3.6.1]

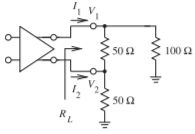
    clipboard_e9cbb2cffac64acdf00860e0d7c59306b.png

    Figure \(\PageIndex{7}\)

    1. What is the differential load impedance?
    2. What is the odd-mode load impedance?
    3. What is the common-mode load impedance?
    4. What is the even-mode load impedance?
    1. A pseudo-differential amplifier is shown in Figure 3.7.3. Distributed biasing of this amplifier (replacing the inductors and \(R_{DD}\)), presents a common-mode impedance of \(5\:\Omega\) and a differential-mode impedance of \(1\text{ k}\Omega\) to the drain terminals of the transistors in the middle of the amplifier band. The transconductance of each transistor is \(g_{m} = 1\text{ S}\), and the internal parasitics of the transistors can be ignored.
      1. Draw the common-mode amplifier schematic without the biasing elements. Include the common-mode load resistance \(R_{Lc}\).
      2. Draw the odd-mode amplifier schematic without the biasing elements. Include the odd-mode load resistance \(R_{Lo}\).
      3. Draw the even-mode amplifier schematic without the biasing elements. Include the odd-mode load resistance \(R_{Lo}\).
      4. Draw the differential-mode amplifier schematic without the biasing elements. Include the common-mode load resistance \(R_{Lc}\).
      5. What is the common-mode gain?
      6. What is the differential-mode gain?
      7. What is the common-mode rejection ratio in decibels?
    2. A pseudo-differential amplifier is shown in Figure 3.7.3. Distributed biasing of this amplifier (replacing the inductors and \(R_{DD}\)), presents a common-mode impedance of \(5\:\Omega\) and an odd-mode impedance of \(1\text{ k}\Omega\) to the drain terminals of the transistors in the middle of the amplifier band. The transconductance of each transistor is \(g_{m} = 100\text{ mS}\) and the internal parasitics of the transistors can be ignored.
      1. Draw the common-mode amplifier schematic without the biasing elements. Include the common-mode load resistance \(R_{Lc}\).
      2. Draw the odd-mode amplifier schematic without the biasing elements. Include the odd-mode load resistance \(R_{Lo}\).
      3. Draw the even-mode amplifier schematic without the biasing elements. Include the odd-mode load resistance \(R_{Lo}\).
      4. Draw the differential-mode amplifier schematic without the biasing elements. Include the common-mode load resistance \(R_{Lc}\).
      5. What is the even-mode impedance presented to the amplifier?
      6. What is the differential-mode impedance presented to the amplifier?
      7. What is the even-mode voltage gain?
      8. What is the differential-mode voltage gain?
      9. What is the common-mode voltage gain?
      10. What is the odd-mode voltage gain?
      11. What is the common-mode rejection ratio?

    3.11.1 Exercises By Section

    \(†\)challenging, \(‡\)very challenging

    \(§3.2\: 1†, 2, 3\)

    \(§3.5\: 4‡, 5‡, 6†, 7†, 8†, 9†\)

    \(§3.6\: 10, 11, 12, 13, 14, 15, 16†, 17†, 18†, 19†, 20, 21, 22, 23†, 24†\)

    \(§3.7\: 25†, 26†\)

    3.11.2 Answers to Selected Exercises

    1. (d) \(34.7\:\Omega\)
    1. (b) \(121\)
    1. (d) \(1/f^{2}\)
    1. (c)
      \(\begin{array}{l}{8\text{ GHz}, -2.77\text{ dB}}\\{9\text{ GHz}, -0.57\text{ dB}} \\ {10\text{ GHz}, 0\text{ dB}}\\{11\text{ GHz}, -0.33\text{ dB}}\\{12\text{ GHz}, -1.03\text{ dB}}\end{array}\)
    1. (h) \(-100\)
    1. (b) \(-3\text{ dB}\)
    2. \(37.5\:\Omega\)
    1. (a)
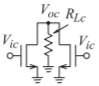
      clipboard_ed49c3699bb4da09f9cd43dc8db7cfb9d.png
      Figure \(\PageIndex{8}\)

    3.11: Exercises is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
    2. Tags
      This page has no tags.