3.2: LAPLACE TRANSFORMS
- Page ID
- 58442
A complete discussion is presented in M. F. Gardner and J. L. Barnes, Transients in Linear Systems, Wiley, New York, 1942.
In this section we temporarily suspend the variable and subscript notation used else where and conform to tradition by using a lower-case variable to signify a time function and the corresponding capital for its transform.
Laplace Transforms offer a method for solving any linear, time-invariant differential equation, and thus can be used to evaluate the response of a linear system to an arbitrary input. Since it is assumed that most readers have had some contact with this subject, and since we do not intend to use this method as our primary analytic tool, the exposure presented here is brief and directed mainly toward introducing notation and definitions that will be used later.
Definitions and Properties
The Laplace transform of a time function \(f(t)\) is defined as
\[\mathcal{L} [f(t)] \triangleq F(s) \triangleq \int_{0}^{\infty} f(t) e^{-st} dt \nonumber \]
where \(s\) is a complex variable \(\sigma + j \omega\). The inverse Laplace transform of the complex function \(F(s)\) is
\[\mathcal{L}^{-1} [F(s)] \triangleq f(t) \triangleq \dfrac{1}{2\pi j} \int_{\sigma_1 - j\infty}^{\sigma_1 + j \infty} F(s) e^{st} ds \nonumber \]
The direct-inverse transform pair is unique(There are three additional constraints called the Direchlet conditions that are satisfied for all signals of physical origin. The interested reader is referred to Gardner and Barnes.) so that
\[\mathcal{L}^{-1} \mathcal{L} [f(t)] = f(t)\label{eq3.2.3} \]
if \(f(t) = 0\), \(t < 0\), and if \(\int_{0}^{\infty} |f(t)| e^{-\sigma_1 t} dt\) is finite for some real value of \(\sigma_1\).
A number of theorems useful for the analysis of dynamic systems can be developed from the definitions of the direct and inverse transforms for functions that satisfy the conditions of Equation \(\ref{eq3.2.3}\). The more important of these theorems include the following.
- Linearity
\[\mathcal{L} [af(t) + bg(t)] = [aF(s) + bG(s)]\nonumber \]
where \(a\) and \(b\) are constants. - Differentiation
\[\mathcal{L} \left [\dfrac{df(t)}{dt} \right ] = sF(s) - \lim_{t \to 0^+} f(t) \nonumber \]
(The limit is taken by approaching \(t = 0\) from positive \(t\).) - Integration
\[\mathcal{L} \left [\int_{0}^{t} f(\tau) d\tau \right ] = \dfrac{F(s)}{s}\nonumber \] - Convolution
\[\mathcal{L} \left [\int_{0}^{t} f(\tau) g(t - \tau) d\tau \right ] = \mathcal{L} \left [\int_{0}^{t} f(t - \tau) g(\tau) d \tau \right ] = F(s) G(s) \nonumber \] - Time shift
\[\mathcal{L} [ f(t - \tau)] = F(s) e^{-s\tau}\nonumber \]
if \(f(t - \tau) = 0\) for \((t - \tau) < 0\), where \(\tau\) is a positive constant. - Time scale
\[\mathcal{L} [f(at)] = \dfrac{1}{a} F \left [\dfrac{s}{a} \right ]\nonumber \]
where \(a\) is a positive constant. - Initial value
\[\lim_{t \to 0^+} f(t) = \lim_{s \to \infty} sF(s)\nonumber \] - Final value
\[\lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s)\nonumber \]
Theorem 4 is particularly valuable for the analysis of linear systems, since it shows that the Laplace transform of a system output is the product of the transform of the input signal and the transform of the impulse response of the system.
Transforms of Common Functions
The defining integrals can always be used to convert from a time function to its transform or vice versa. In practice, tabulated values are frequently used for convenience, and many mathematical or engineering references(See, for example, A. Erdeyli (Editor) Tables of Integral Transforms, Vol. 1, Bateman Manuscript Project, McGraw-Hill, New York, 1954 and R. E. Boly and G. L. Tuve, (Editors), Handbook of Tables for Applied Engineering Science, The Chemical Rubber Company, Cleveland, 1970.) contain extensive lists of time functions and corresponding Laplace transforms. A short list of Laplace transforms is presented in Table 3.1.
The time functions corresponding to ratios of polynomials in \(s\) that are not listed in the table can be evaluated by means of a partial fraction expansion. The function of interest is written in the form
\[F(s) = \dfrac{p(s)}{q(s)} = \dfrac{p(s)}{(s + s_1)(s + s_2) \cdots (s + s_n)} \nonumber \]
It is assumed that the order of the numerator polynomial is less than that of the denominator. If all of the roots of the denominator polynomial are first order (i.e., \(s_i \ne s_j\), \(i \ne j\)),
\[F(s) = \sum_{k = 1}^{n} \dfrac{A_k}{s + s_k} \label{eq3.2.5} \]
where
\[A_k = \lim_{s \to -s_k} [(s + s_k) F(s)] \label{eq3.2.6} \]
If one or more roots of the denominator polynomial are multiple roots, they contribute terms of the form
\[\sum_{k = 1}^{m} \dfrac{B_k}{(s + s_i)^k} \label{eq3.2.7} \]
Table 3.1 Laplace Transform Pairs
| \(F(s)\) | \(f(t), t \ge 0\) \([f(t) = 0, t < 0]\) |
| 1 | Unit impulse \(u_0 (t)\) |
| \(\dfrac{1}{s}\) | Unit step \(u_{-1} (t)\) \([f(t) = 1, t \ge 0]\) |
| \(\dfrac{1}{s^2}\) | Unit step \(u_{-2} (t)\) \([f(t) = 1, t \ge 0]\) |
| \(\dfrac{1}{s^{n + 1}}\) | \(\dfrac{t^n}{n!}\) |
| \(\dfrac{1}{s + a}\) | \(e^{-at}\) |
| \(\dfrac{1}{(s + a)^{n + 1}}\) | \(\dfrac{t^n}{(n)!} e^{-at}\) |
| \(\dfrac{1}{s(\tau s + 1)}\) | \(1 - e^{-t/\tau}\) |
| \(\dfrac{\omega}{(s + a)^2 + \omega^2}\) | \(e^{-at} \sin \omega t\) |
| \(\dfrac{s + a}{(s + a)^2 + \omega^2}\) | \(e^{-at} \cos \omega t\) |
| \(\dfrac{1}{s^2/\omega_n^2 + 2 \zeta s/\omega_n + 1}\) | \(\dfrac{\omega_n}{\sqrt{1 - \zeta^2}} e^{-\zeta \omega_n t} (\sin \omega_n \sqrt{1 - \zeta^2} t), \zeta < 1\) |
| \(\dfrac{1}{s(s^2/\omega_n^2 + 2 \zeta s/\omega_n + 1)}\) | \(1 - \dfrac{e^{-zeta \omega_n t}}{\sqrt{1 - \zeta^2}} \sin \left [\omega_n \sqrt{1 - \zeta^2} t + \tan^{-1} \left (\dfrac{\sqrt{1 - \zeta^2}}{\zeta} \right ) \right ], \zeta < 1\) |
where \(m\) is the order of the multiple root located at \(s = -s_i\). The \(B\)'s are determined from the relationship
\[B_k = \lim_{s \to -s_i} \left \{\dfrac{1}{(m - k)!} \dfrac{d^{m-k}}{ds^{m - k}} [(s + s_i)^m F(s)] \right \} \label{eq3.2.8} \]
Because of the linearity property of Laplace transforms, it is possible to find the time function \(f(t)\) by summing the contributions of all components of \(F(s)\).
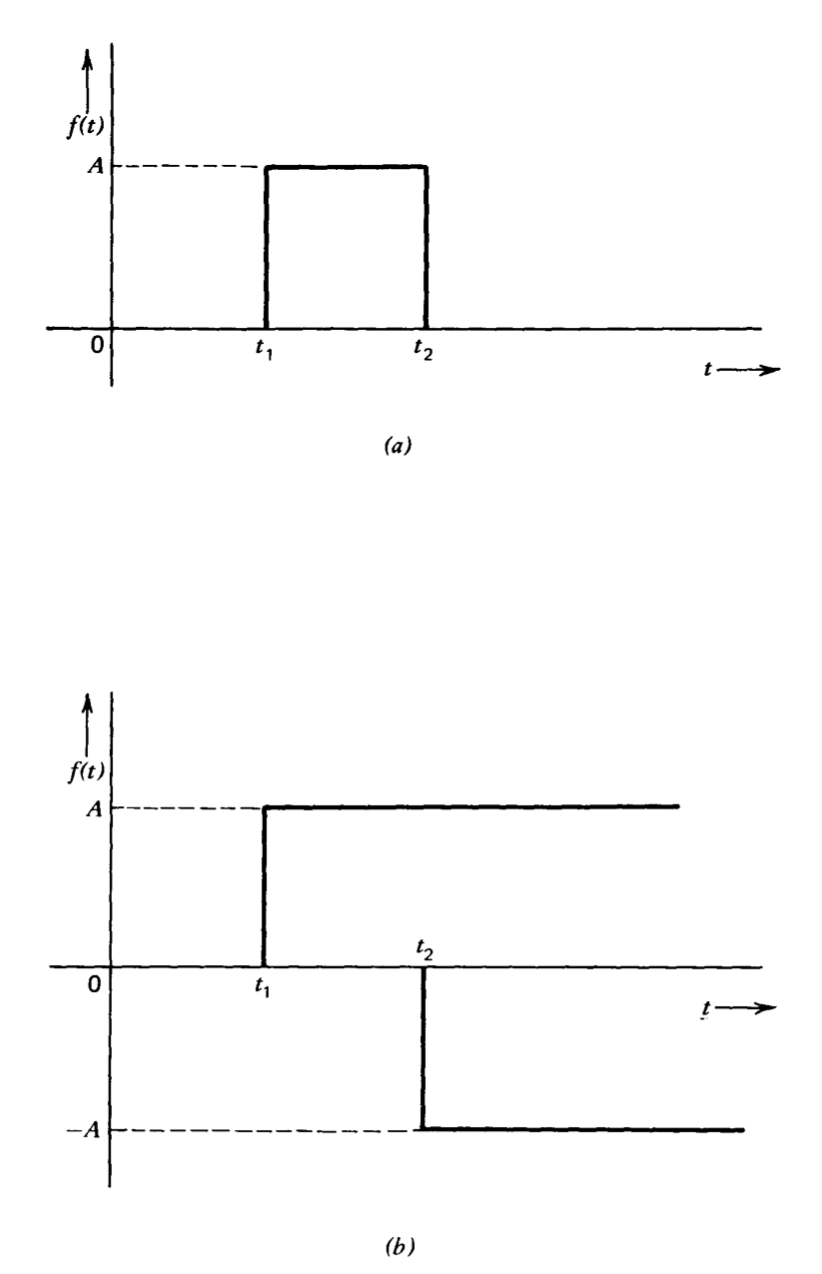
The properties of Laplace transforms listed earlier can often be used to determine the transform of time functions not listed in the table. The rectangular pulse shown in Figure 3.3 provides one example of this technique. The pulse (Figure 3.3a) can be decomposed into two steps, one with an amplitude of \(+A\) starting at \(t = t_1\), summed with a second step of amplitude \(-A\) starting at \(t = t_2\). Theorems 1 and 5 combined with the transform of a unit step from Table 3.1 show that the transform of a step with amplitude \(A\) that starts at \(t = t_1\) is \((A/s)e^{-st_1}\). Similarly, the transform of the second component is \(-(A/s) e^{-st_2}\). Superposition insures that the transform of \(f(t)\) is the sum of these two functions, or
\[F(s) = \dfrac{A}{s} (e^{-st_1} - e^{-st_2}) \nonumber \]
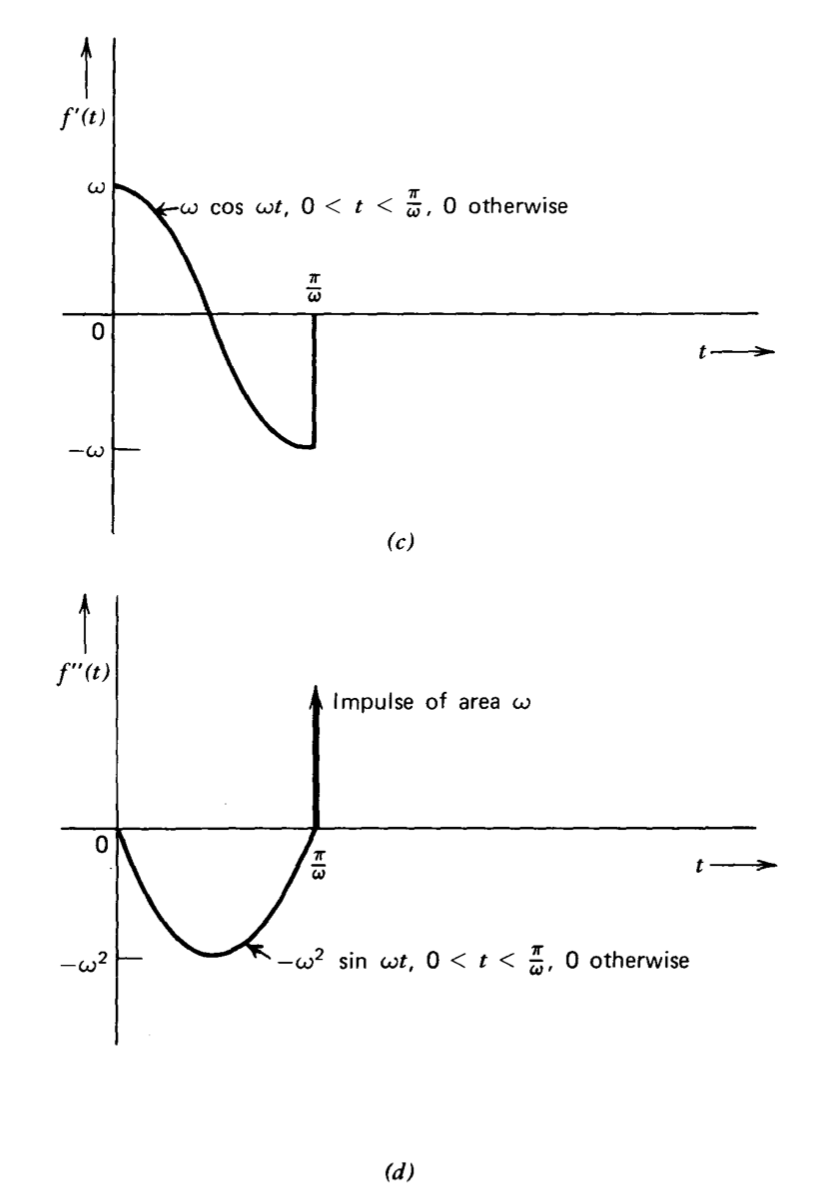
The sinusoidal pulse shown in Figure 3.4 is used as a second example. One approach is to represent the single pulse as the sum of two sinusoids exactly as was done for the rectangular pulse. Table 3.1 shows that the transform of a unit-amplitude sinusoid starting at time \(t = 0\) is \(\omega/ (s^2 + \omega^2)\). Summing transforms of the components shown in Figure 3.4\(b\) yields
\[F(s) = \dfrac{\omega}{s^2 + \omega^2} [1 + e^{-s(\tau /\omega)}] \nonumber \]
An alternative approach involves differentiating \(f(t)\) twice. The derivative of \(f(t)\), \(f'(t)\), is shown in Figure 3.4\(c\). Since \(f(0) = 0\), theorem 2 shows that
\[\mathcal{L} [f'(t)] = sF(s) \nonumber \]
The second derivative of \(f(t)\) is shown in Figure 3.4\(d\). Application of theorem 2 to this function(The portion of this expression involving \(\lim t \to 0^+\) could be eliminated if a second impulse \(\omega u_0 (t)\) were included in \(f''(t)\).) leads to
\[\mathcal{L} [f'' (t)] = s \mathcal{L} [f'(t)] - \lim_{t \to 0^+} f'(t) = s^2 F(s) - \omega \label{eq3.2.12} \]
However, Figure 3.4\(d\) indicates that
\[f''(t) = -\omega^2 f(t) + \omega u_0 \left (t - \dfrac{\pi}{\omega} \right ) \nonumber \]
Thus
\[\mathcal{L} [f'' (t)] = -\omega^2 F(s) + \omega e^{-s(\pi/\omega)} \label{eq3.2.14} \]
Combining Equations \(\ref{eq3.2.12}\) and \(\ref{eq3.2.14}\) yields
\[s^2 F(s) - \omega = -\omega^2 F(s) + \omega e^{-s (\pi/\omega)} \label{eq3.2.15} \]
Equation \(\ref{eq3.2.15}\) is solved for \(F(s)\) with the result that
\[F(s) = \dfrac{\omega}{s^2 + \omega^2} [1 + e^{-s (\pi/ \omega)}] \nonumber \]
Note that this development, in contrast to the one involving superposition, does not rely on knowledge of the transform of a sinusoid, and can even be used to determine this transform.
Examples of the Use of Transforms
Laplace transforms offer a convenient method for the solution of linear, time-invariant differential equations, since they replace the integration and differentiation required to solve these equations in the time domain by algebraic manipulation. As an example, consider the differential equation
\[\dfrac{d^2 x}{dt^2} + 3 \dfrac{dx}{dt} + 3x = e^{-t} \ \ t > 0 \label{eq3.2.17} \]
subject to the initial conditions
\[x(0^+) = 2 \ \ \ \dfrac{dx}{dt} (0^+) = 0 \nonumber \]
The transform of both sides of Equation \(\ref{eq3.2.17}\) is taken using theorem 2 (applied twice in the case of the second derivative) and Table 3.1 to determine the Laplace transform of \(e^{-t}\).
\[s^2 X(s) - sx (0^+) - \dfrac{dx}{dt} (0^+) + 3sX(s) - 3x (0^+) + 2X(s) = \dfrac{1}{s + 1} \nonumber \]
Collecting terms and solving for \(X(s)\) yields
\[X(s) = \dfrac{2s^2 + 8s + 7}{(s + 1)^2 (s + 2)} \nonumber \]
Equations \(\ref{eq3.2.5}\) and \(\ref{eq3.2.7}\) show that since there is one first-order root and one second-order root,
\[X(s) = \dfrac{A_1}{(s + 2)} + \dfrac{B_1}{(s + 1)} + \dfrac{B_2}{(s + 1)^2} \nonumber \]
The coefficients are evaluated with the aid of Equations \(\ref{eq3.2.6}\) and \(\ref{eq3.2.8}\), with the result that
\[X(s) = \dfrac{-1}{s + 2} + \dfrac{3}{s + 1} + \dfrac{1}{(s + 1)^2} \nonumber \]
The inverse transform of \(X(s)\), evaluated with the aid of Table 3.1, is
\[x(t) = -e^{-2t} + 3e^{-t} + te^{-t} \nonumber \]
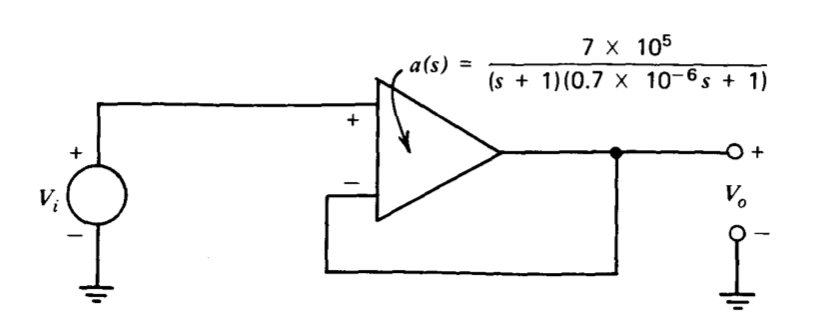
The operational amplifier connected as a unity-gain noninverting amplifier (Figure 3.5) is used as a second example illustrating Laplace techniques. If we assume loading is negligible,
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{a(s)}{1 + a(s)} = \dfrac{7 \times 10^5}{(s + 1)(0.7 \times 10^{-6} s + 1) + 7 \times 10^5} \simeq \dfrac{1}{10^{-12} s^2 + 1.4 \times 10^{-6} s + 1} \nonumber \]
If the input signal is a unit step so that \(V_i (s)\) is \(1/s\),
\[V_o (s) = \dfrac{1}{s (10^{-12} s^2 + 1.4 \times 10^{-6} s + 1)} = \dfrac{1}{s[s^2/(10^6)^2 + 2(0.7)s/10^6 + 1]}\label{eq3.2.24} \]
The final term in Equation \(\ref{eq3.2.24}\) shows that the quadratic portion of the expression has a natural frequency \(\omega_n = 10^6\) and a damping ratio \(\zeta = 0.7\). The corresponding time function is determined from Table 3.1, with the result
\[f(t) = 1 - \dfrac{e^{-0.7 \times 10^6 t}}{0.7} \sin (0.7 \times 10^6 t + 45^{\circ}) \nonumber \]


