11.5: NONLINEAR CONNECTIONS
- Page ID
- 75050
The topologies presented in Section 11.4 were intended to provide linear gains, transfer functions, or impedances. While practical realizations of these circuits may include nonlinear elements, the feedback is arranged to minimize the effects of such nonlinearities. In many other cases feedback implemented by means of operational amplifiers is used to augment, control, or idealize the characteristics of nonlinear elements. Examples of these types of applications are presented in this section.
Precision Rectifiers
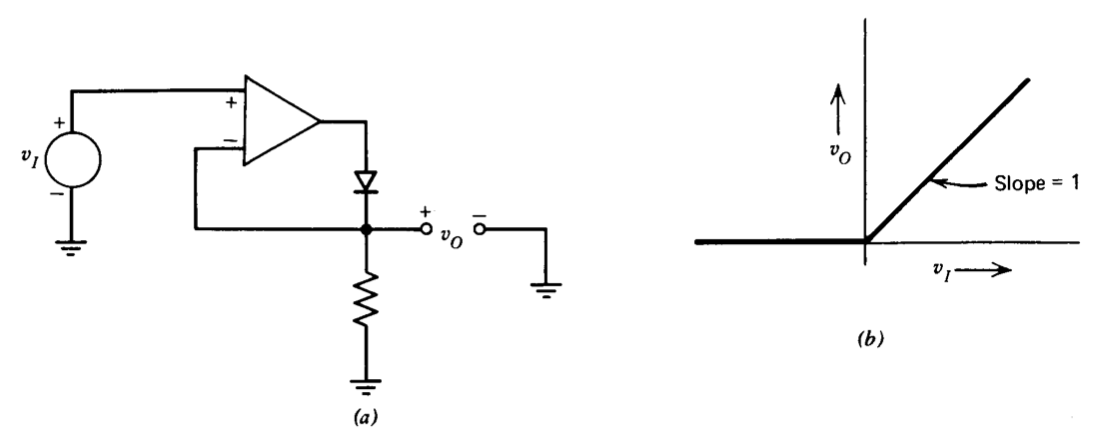
Many circuit connections use diodes to rectify signals. However, the forward voltage drop associated with a diode limits its ability to rectify low level signals. The combination of a diode with an operational amplifier (Figure 11.18) results in a circuit with a much lower threshold. Operation depends on the fact that the diode-amplifier combination can only pull the output voltage positive, so that negative input voltages result in zero output. With a positive input voltage, a negligibly small differential signal (equal to the threshold voltage of the diode divided by the open-loop gain of the amplifier) is amplified to provide sufficient amplifier output voltage to overcome the diode threshold, with the result that
\[v_O = v_I \ \ \ \ v_I > 0 \nonumber \]
\[v_O = 0 \ \ \ \ v_I < 0 \nonumber \]
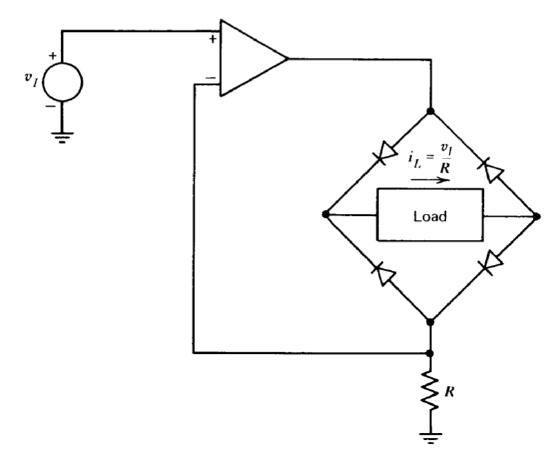
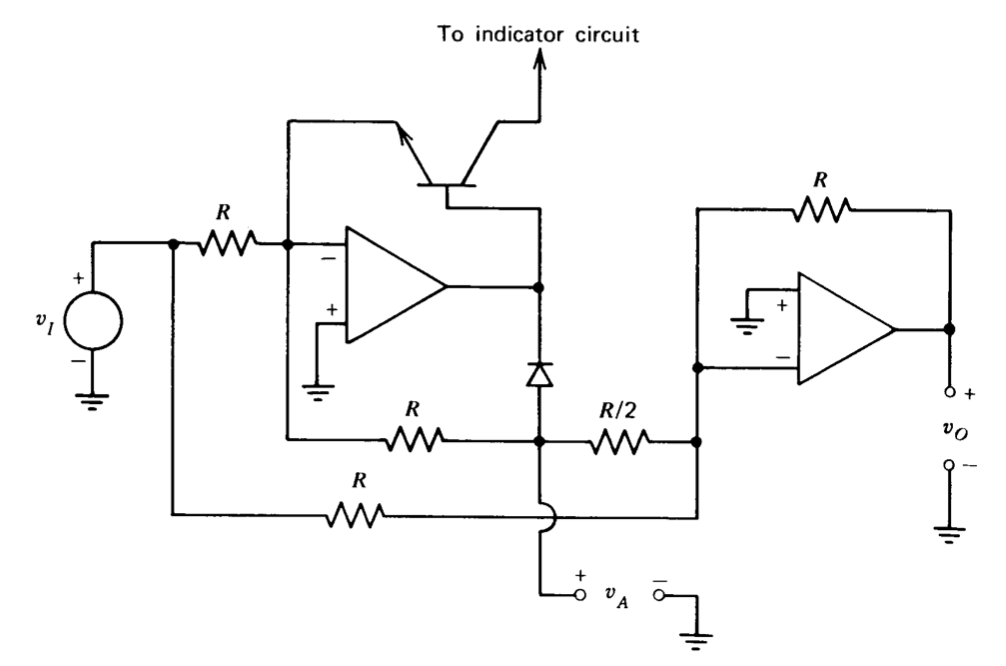
Many variations of this precision rectifier or "superdiode" exist. For example, the circuit shown in Figure 11.19 rectifies and provides a current- source drive for a floating load such as a D'Arsonval meter movement. Figure 11.20 illustrates another rectifier circuit. With \(v_I\) negative, voltage \(v_A\) is zero, and \(v_O = - v_I\) because of the inversion provided by the right- hand amplifier. The transistor provides a feedback path for the first ampli fier so that it remains in its linear region for negative inputs. Operation in the linear region keeps the inverting input of the first amplifier at ground potential, thereby preventing the input signal from driving voltage \(v_A\) via direct resistive feedthrough. Maintaining linear-region operation also elimi nates the long amplifier recovery times that frequently accompany overload and saturation. While a diode could be used in place of the transistor, the transistor provides a convenient method for driving further amplifying cir cuits, which indicate input-signal polarity if this function is required. For positive input voltages, voltage \(v_A = - v_I\), so that the resistor with value \(R/2\) also applies current to the input of the second amplifier, with the result that
\[v_O = -(v_I - 2v_I) = v_I \ \ \ \ v_I > 0 \nonumber \]
\[v_O = -v_I \ \ \ \ \ \ \ \ \ \ \ v_I < 0 \nonumber \]
Peak Detector
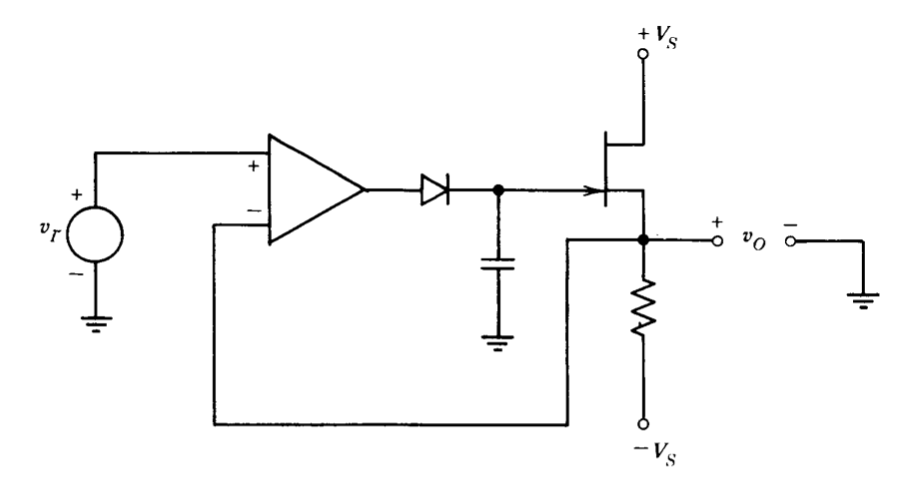
The peak-detector circuit shown in Figure 11.21 illustrates a further elaboration on the general theme of minimizing the effects of voltage drops in various elements by including these drops inside a feedback loop. If the output voltage is more positive than the input voltage, the output of the operational amplifier will be saturated in the negative direction. (Some form of clamping may be included to speed recovery from this state.) Under these conditions, the capacitor current consists only of diode and FET-gate leakage currents; thus the capacitor voltage changes very slowly. As a matter of practical concern, the circuit will function properly only if current levels are such that the capacitor voltage drifts negatively in this state. Otherwise, the connection will eventually saturate at its maximum positive output level.
If \(v_I\) becomes greater than \(v_O\), the capacitor is charged rapidly from the output of the operational amplifier via the diode until equality is reestablished. Note that the capacitor voltage is not forced to be equal to \(v_I\), but rather to be equal to a voltage that, combined with the FET gate-to-source voltage, forces equality between \(v_O\) and \(v_I\). In this way the output voltage "remembers" the most positive value of the input signal.
Generation of Piecewise-Linear Transfer Characteristics
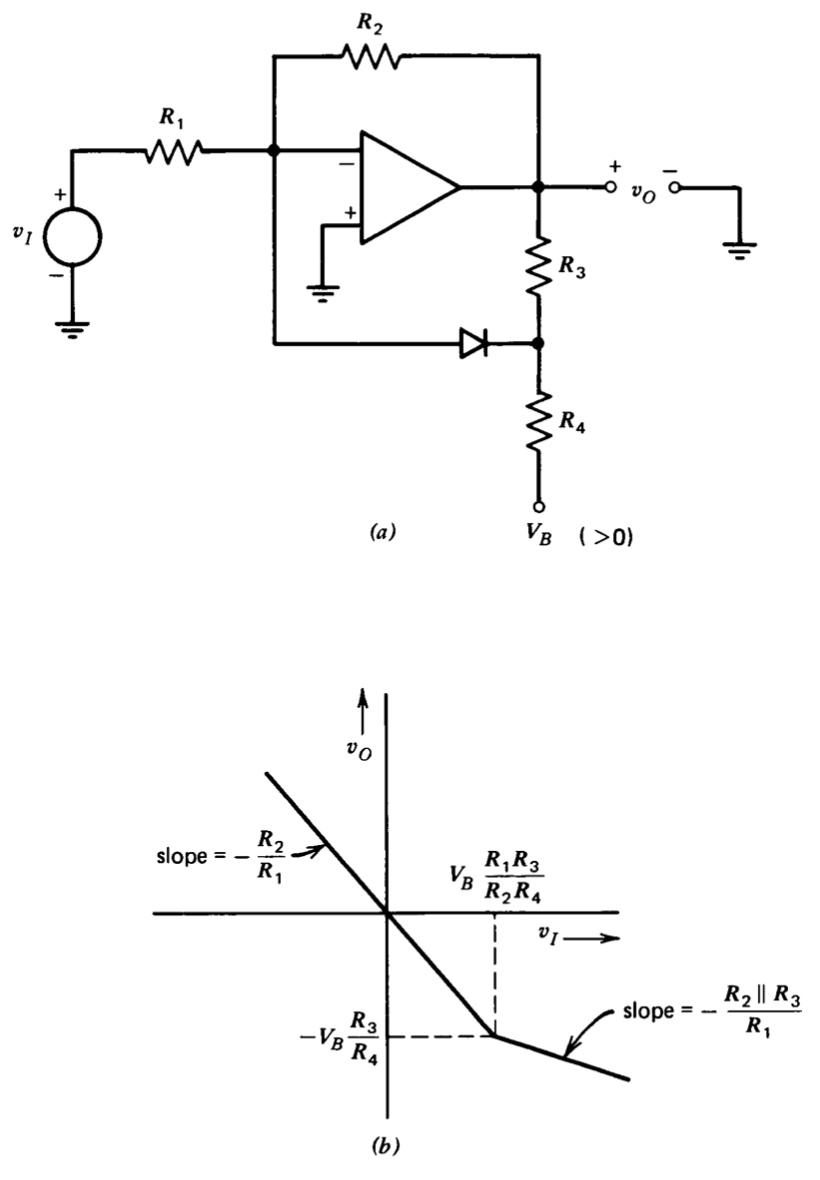
Diodes can be combined with operational amplifiers to realize signal- shaping circuits other than rectifiers. Figure 11.22 shows a circuit that pro vides a compressive or limiting-type nonlinear transfer relationship. For input voltages more negative than \(V_B (R_1R_3/R_2 R_4)\) the diode is an open circuit, and the incremental gain of the circuit is \(-R_2/R_1\). When \(v_I = V_B(R_1R_3/R_2 R_4)\), the diode is on the threshold of conduction. Assuming a "perfect" diode (zero threshold voltage and zero on resistance in the forward direction), the effective feedback resistance for further increases in input voltage is \(R_2 || R_3\), and the magnitude of the incremental gain decreases to \(-(R_2 || R_3)/R_1\).
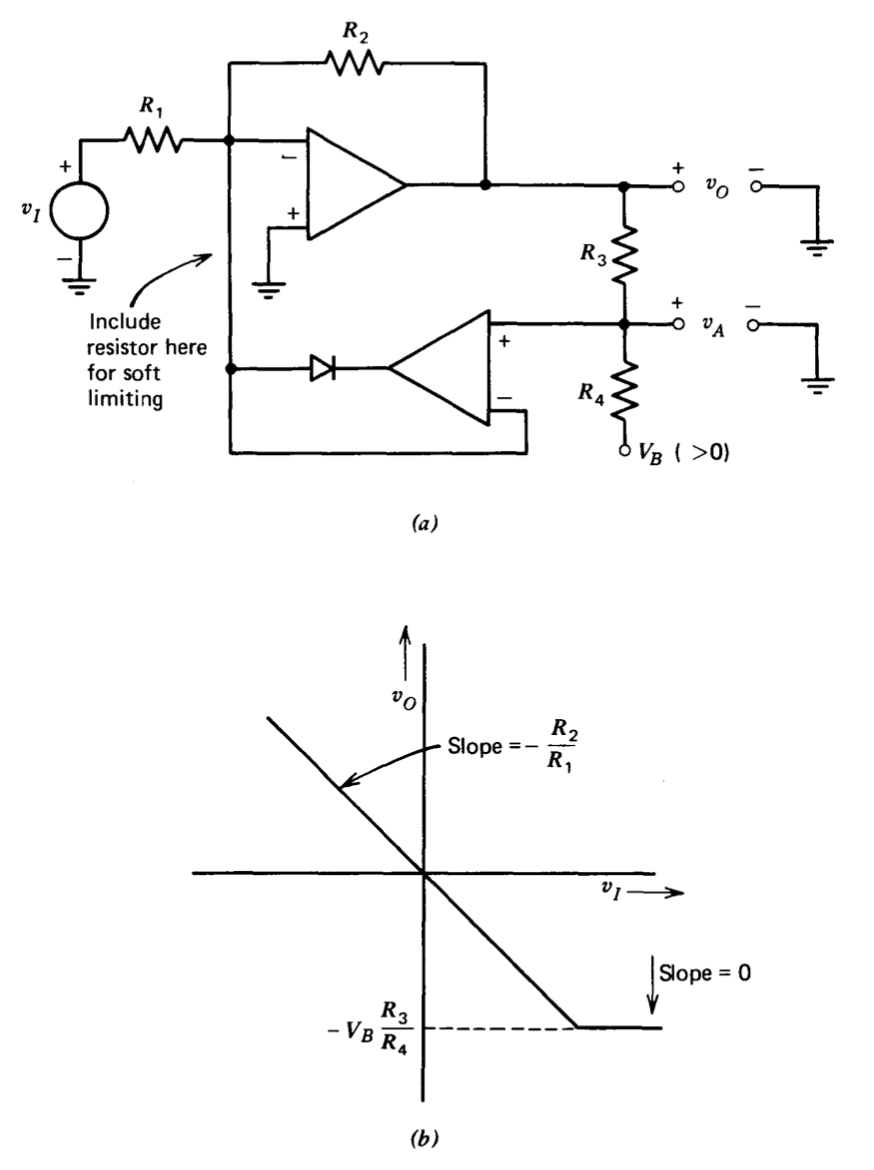
The operation of the limiter was described assuming perfect diode char acteristics. If the performance degradation that results from actual diode characteristics is intolerable, a "superdiode" connection can be used as shown in Figure 11.23. The lower operational amplifier cannot affect circuit operation for the positive values of VA that correspond to input voltages more negative than \(V_B (R_1R_3/R_2R_4)\) because the diode in series with its output is reverse biased. However, the lower amplifier can supply as much current as is required to keep the voltage at the junction of \(R_3\) and \(R_4\) from becoming negative, and thus this circuit provides hard limiting with the incremental gain dropping to zero for input voltages more positive than the threshold level. If softer limiting is required, a resistor can be included at the indicated point.
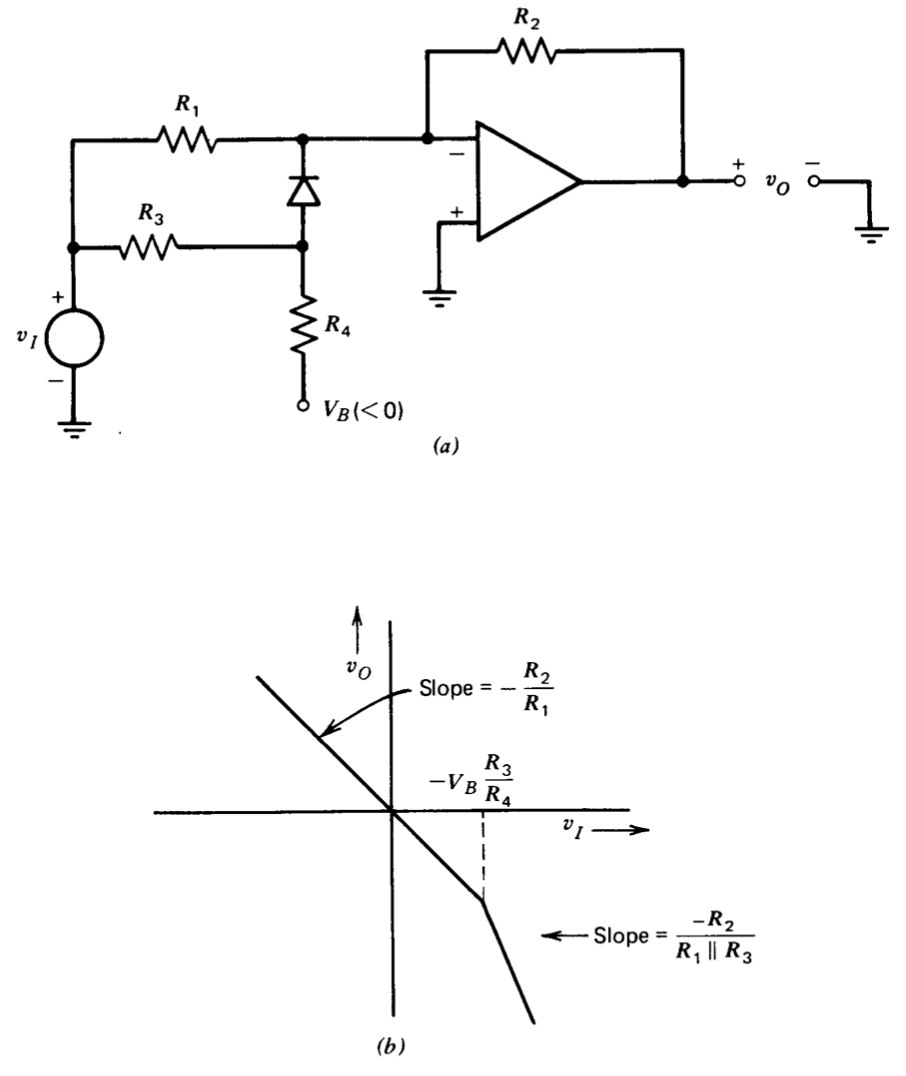
It is clear that additional resistor networks and diodes (or superdiodes) can be added to increase the number of break points in the transfer characteristics. However, the topology of Figure 11.22 or Figure 11.23 precludes increasing the magnitude of the incremental gain as input-voltage magnitude increases. Shifting the diode-resistor network to the amplifier input circuit (Figure 11.24) is one way that expansive-type nonlinearities can be realized.
Antilog Circuits

The exponential current-voltage characteristics of diodes or transistors can be exploited to realize circuits with exponential or logarithmic characteristics. Figure 11.25 illustrates a very simple circuit that provides a logarithmic relationship between output voltage and input current. Under normal operating conditions, the operational amplifier keeps the collector-to-base voltage of the transistor at zero. As a result, collector-to-base junction leakage currents are eliminated as are base-width modulation effects, and many types of transistors will accurately follow the relationship
\[i_C \simeq I_S e^{qv_{BE}/kT} \label{eq11.5.5} \]
over a range of operating current levels that extends from picoamperes to a fraction of a milliamp. Deviation from purely exponential behavior occurs at current levels comparable to \(I_S\) and at current levels where ohmic resistances become significant.(Theoretically, a diode could be used as a feedback element as indicated in Section 1.2.3 to obtain logarithmic closed-loop characteristics. In practice, the transistor connection illustrated here is preferable, since transistors generally display the desired characteristics over a far larger dynamic range than do diodes.)
For this circuit topology, \(V_{BE} = - v_O\), and feedback keeps \(i_C = i_I\). Substituting these constraints into Equation \(\ref{eq11.5.5}\) shows that
\[i_I = I_S e^{-q v_O/kT} \nonumber \]
or, if we solve for \(v_O\),
\[v_O = -\dfrac{kT}{q} \ln \dfrac{i_I}{I_S} \nonumber \]
Of course, the current applied to this circuit can be derived from an available input voltage via a resistor connected to the inverting input terminal of the operational amplifier. In this case, the voltage offset of the operational amplifier contributes an error term that normally limits dynamic range to three or four orders of magnitude. If the input signal is available as a current, as it is for some sensors such as ionization gauges, much wider dynamic range is possible for sufficiently low amplifier bias current.

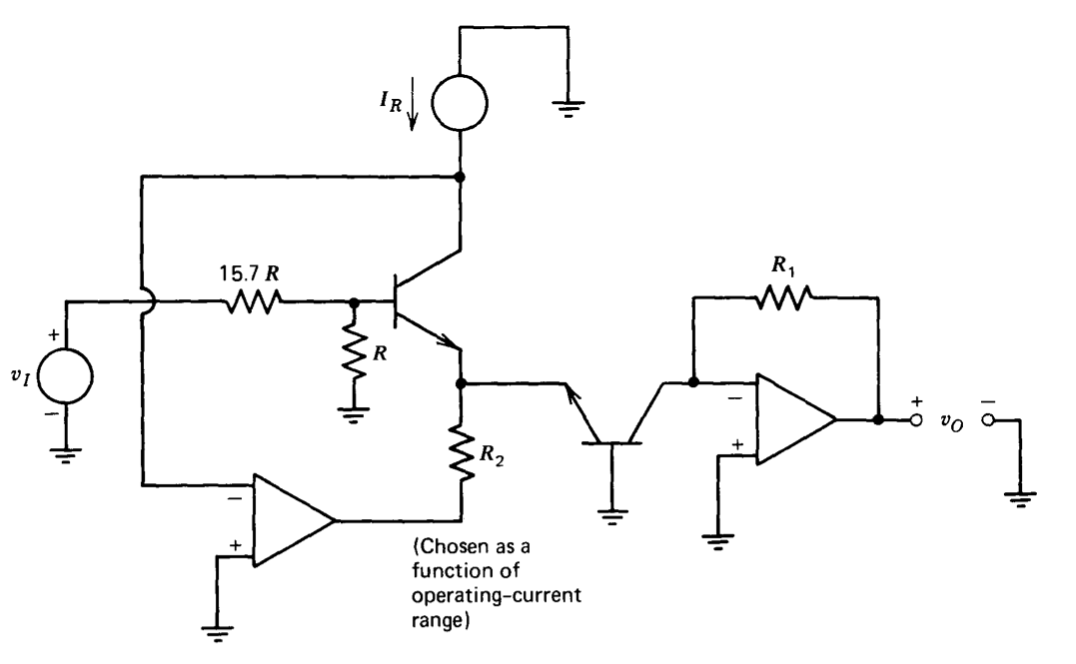
One shortcoming of this simple circuit is that the quantity \(I_S\) is highly temperature dependent (see Section 7.2). The circuit shown in Figure 11.26 offers improved performance with temperature. Feedback through the right-hand operational amplifier keeps the collector current of \(Q_2\) equal to the reference current \(I_R\); thus
\[v_{BE2} = \dfrac{kT}{q} \ln \dfrac{I_R}{I_{S2}} \label{eq11.5.8} \]
Note that, since the potential at the collector of \(Q_2\) is held at zero volts by the operational amplifier, the reference current is easily obtained via a resistor connected to a positive supply voltage.
The left-hand operational amplifier adjusts the base voltage of \(Q_2\), thereby changing the base-to-emitter voltage of \(Q_1\) until the collector current of \(Q_1\) equals \(i_I\), with the result that
\[v_{BE1} = \dfrac{kT}{q} \ln \dfrac{i_I}{I_{S1}} \nonumber \]
If values are selected so that the base current of \(Q_2\) does not load the base-circuit attenuator, the voltage relationship is
\[v_{BE1} = v_{BE2} - \dfrac{1}{16.7} v_O \label{eq11.5.10} \]
Combining Equations \(\ref{eq11.5.8}\) through \(\ref{eq11.5.10}\) and solving for \(v_O\) yields
\[v_O = -16.7 \dfrac{kT}{q} \left [ \ln \dfrac{i_I}{I_{S1}} - \ln \dfrac{I_R}{I_{S2}} \right ] = -16.7 \dfrac{kT}{q} \ln \left [ \dfrac{i_I}{i_R} \dfrac{I_{S2}}{I_{S1}} \right ] \label{eq11.5.11} \]
If transistors \(Q_1\) and \(Q_2\) have well-matched values of \(I_S\), Equation \(\ref{eq11.5.11}\) becomes
\[v_O = -16.7 \dfrac{kT}{q} \ln \left [\dfrac{i_I}{i_R} \right ] \label{eq11.5.12} \]
The resistive-divider attenuation ratio of 16.7 is used so that at room temperature, Equation \(\ref{eq11.5.12}\) reduces to
\[v_O = -1 \text{ volt }\log_{10} \left [\dfrac{i_I}{i_R} \right ] \nonumber \]
While the use of matched transistors as shown in Figure 11.26 does eliminate the dependence of the output on \(I_S\), Equation \(\ref{eq11.5.12}\) shows that the scale factor of the circuit is proportional to absolute temperature. One common solution is to compensate by using a resistor with a value inversely proportional to absolute temperature as the smaller of the two resistors in the voltage divider.
The antilog circuit shown in Figure 11.27 results from rearranging components. The reader should verify that, at room temperature and with matched transistors, the input-output relationship for this circuit is
\[v_O = R_1 I_R \times 10^{-(v_I/\text{1 volt})} \nonumber \]
Analog Multiplication
There are a number of configurations that perform analog multiplication, that is, provide an output voltage proportional to the product of two input voltages. For example, one or more log circuits can be combined with an antilog circuit to realize multipliers, dividers, or circuits that raise a voltage to a power. Another technique known as quarter-square multiplication exploits the relationship
\[(v_X + v_Y)^2 - (v_X - v_Y)^2 = 4 v_X v_Y \nonumber \]
The quadratic transfer characteristics can be approximated with piecewise linear diode-operational amplifier connections.
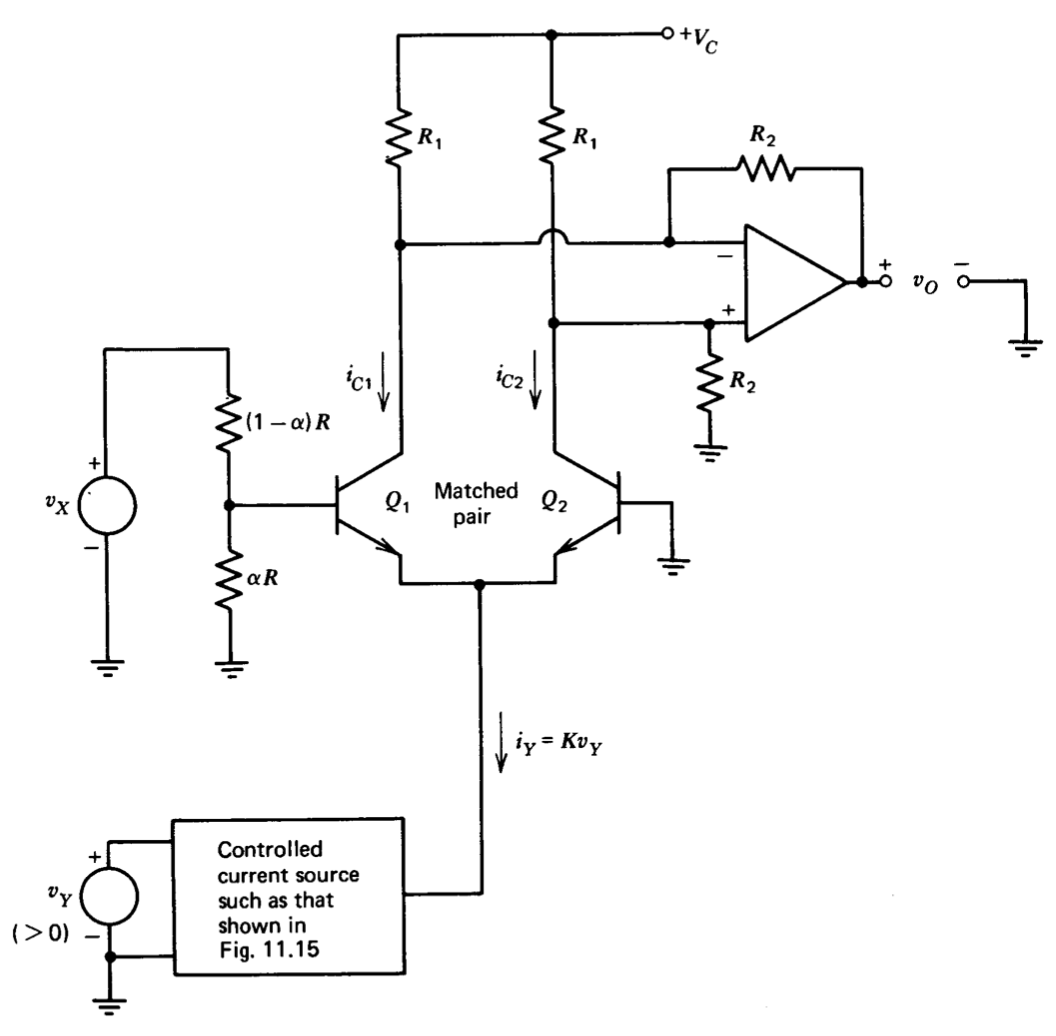
A method known as transconductance multiplication is the basis for several available discrete and integrated-circuit analog multipliers because it is capable of moderate accuracy and requires relatively few components. A simplified transconductance multiplier (limited to two-quadrant operation because the voltage \(v_Y\) cannot be negative) is shown in Figure 11.28.
If it is assumed the \(v_X\) attenuator is not loaded by the input current of transistor \(Q_1\) and that the differential input voltage applied to the pair is small enough so that linear-region relationships are valid for the transistors, the difference between the two collector currents is
\[i_{C1} - i_{C2} = \alpha v_X g_m \label{eq11.5.16} \]
where \(g_m\) is the (equal) transconductance of either transistor.
For small-signal operation, the quantity \(g_m\) is related to quiescent operating current, which is in turn determined by the input variable \(v_Y\). Thus,
\[g_m = \dfrac{i_Y q}{2kT} = \dfrac{Kv_Y q}{2kT} \label{eq11.5.17} \]
Substituting Equation \(\ref{eq11.5.17}\) into Equation \(\ref{eq11.5.16}\) shows that
\[i_{C1} - i_{C2} = \dfrac{\alpha Kq}{2kT} v_X v_Y \label{eq11.5.18} \]
The reader should convince himself that the differentially connected operational amplifier provides an output voltage equal to \(R_2\) times the difference between the two collector currents. Substituting this relationship into Equation \(\ref{eq11.5.18}\) yields
\[v_O = \dfrac{\alpha KR_2q}{2kT} v_X v_Y \label{eq11.5.19} \]
There are a number of design constraints necessary for satisfactory operation or introduced for convenience, including the following.
(a) The current \(i_Y\) is normally limited to a fraction of a milliamp so that performance is not degraded by ohmic transistor resistance.
(b) The attenuation ratio a must be chosen to limit the input voltage applied to the transistor pair to a low level. Detailed calculations show that the inaccuracy attributable to the exponential transistor characteristics can be limited to less than 1% of maximum output if the maximum magnitude of the voltage into the differential pair is kept below approximately \(8\ mV\).
(c) Because of the limited signal levels applied to the differential pair, its drift has a significant effect on overall performance. The circuit can be balanced by adjusting the ratio of the two resistors labeled \(R_1\) in Figure 11.28.
(d) The temperature dependence of Equation \(\ref{eq11.5.19}\) can be compensated for by making the voltage-attenuator ratio or the current-source scale factor temperature dependent.
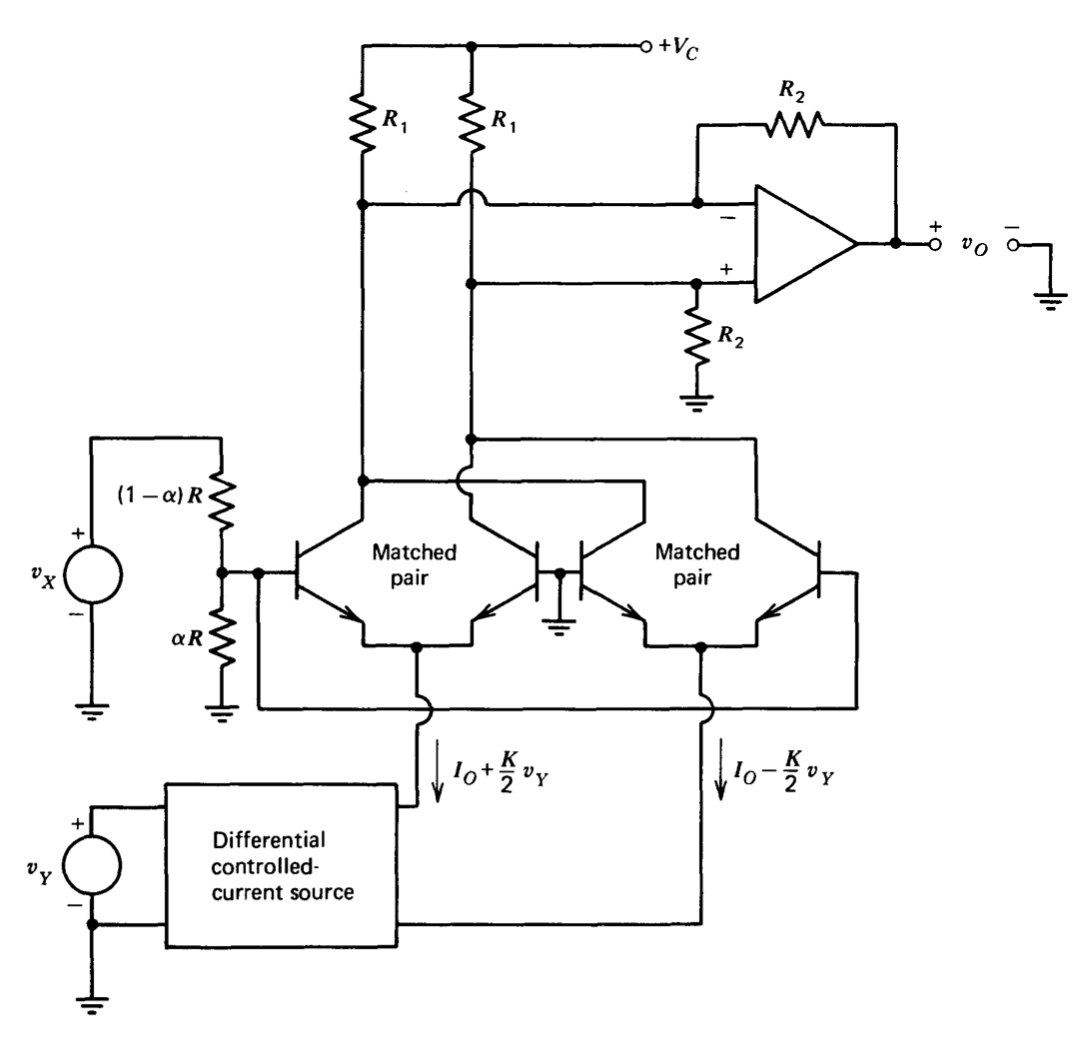
(e) The restriction of single-polarity values for the \(v_Y\) input can be removed by including a second differential pair of transistors, and by making the operating currents of the two pairs vary differentially as a function of \(v_Y\). The interested reader is invited to show that the input-output relationship for the four-quadrant transconductance multiplier shown in Figure 11.29 is given by Equation \(\ref{eq11.5.19}\).
(f) Scale factor is frequently adjusted to give \(v_O = v_Xv_Y/10\) volts, a value compatible with the signal levels common to many analog systems.
In general, achieving highly accurate performance from a transconductance multiplier involves a rather complex series of adjustments to null various sources of error. This process is simplified somewhat by an innovation developed by Gilbert(. Gilbert, "A D.C.-500 MHz Amplifier /Multiplier Principle," Digest of Technical Papers, 1968 Solid-State Circuits Conference, Philadelphia, Pa.) which uses compensating diodes to eliminate scale-factor temperature dependence and to increase the signal levels that may be applied to the differential pairs. While there are problems that must be overcome, the technique is good enough so that several manufacturers offer inexpensive transconductance multipliers with errors from all sources of less than 1% of maximum output.


