6.9: Current Feedback Amplifiers
- Page ID
- 28561
The current feedback amplifier is a unique device in the world of linear integrated circuits. Its prime advantage is that it does not suffer from the strict gain/bandwidth trade-off typical of normal op amps. This means that it is possible to increase its gain without incurring an equal decrease in bandwidth. This has obvious advantages for high-speed applications. Also, these devices tend to be free of slewing effects.
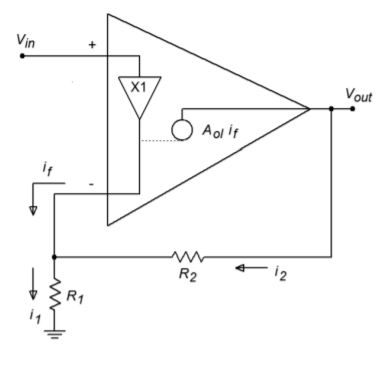
Figure \(\PageIndex{1}\): Current feedback amplifier equivalent.
An equivalent model of a noninverting current feedback amplifier is shown in Figure \(\PageIndex{1}\). This device uses a transimpedance source (i.e., a current-controlled voltage source) to translate the feedback current into an output voltage. Instead of relying on negative feedback to keep the inverting and noninverting terminals at the same potential, the current feedback amplifier utilizes a unity-gain buffer placed between the two inputs. In this manner, the potential that drives the noninverting input must also appear at the inverting input. Also, the buffer exhibits a low output impedance into or out of which the feedback current may flow. From this diagram we may derive the general voltage-gain expression.
By inspection
\[ V_{in} = V_{+} = V_{-} \label{6.21} \]
\[ I_{1} = \frac{V_{in}}{R_1} \label{6.22} \]
\[ I_{2} = \frac{V_{out} – V_{in}}{R_2} \label{6.23} \]
\[I_{f} = I_1 − I_2 \label{6.24} \]
\[ V_{out} = A_{ol} I_f \label{6.25} \]
Combining \ref{6.22}, \ref{6.23}, and \ref{6.24} with \ref{6.25} yields
\[ V_{out} = A_{ol}( \frac{V_{in}}{R_1} − \frac{V_{out}−V_{in}}{R_2} ) \label{6.26} \]
Simplification follows
\[\frac{V_{out}}{A_{ol}} = \frac{V_{in}}{R_1} − \frac{V_{out} – V_{in}}{R_2} \\ \frac{V_{out}}{A_{ol}} = \frac{V_{in} R_2 − V_{out} R_1 + V_{in} R_1}{R_1 R_2} \\ \frac{V_{out} R_1 R_2}{A_{ol}} = V_{in} R_2 − V_{out} R_1 + V_{in} R_1 \\ \frac{V_{out} R_1 R_2}{A_{ol}} + V_{out} R_1 =V_{in} (R_2+R_1) \nonumber \]
\[V_{out}( \frac{R_1 R_2}{A_{ol}} + R_1) = V_{in} (R_2+R_1) \label{6.27} \]
We now solve \ref{6.27} in terms of \(V_{out}/V_{in}\), which is \(A_v\).
\[ \frac{V_{out}}{V_{in}} = \frac{R_1 + R_2}{\frac{R_1 R_2}{A_{ol}} + R_1} \\ A_v = \frac{R_1 + R_2}{\frac{R_1 R_2}{A_{ol}} + R_1} \nonumber \]
\[ A_v = \frac{\frac{R_2}{R_1} + 1}{\frac{R_2}{A_{ol}} + 1} \label{6.28} \]
If, for convenience, we define \(R_2/R_1\) + 1 as G, Equation \ref{6.28} becomes
\[ A_v = \frac{G}{\frac{R_2}{A_{ol}} +1} \label{6.29} \]
If \(A_{ol}\) is sufficiently large, this may be approximated as
\[ A_v = G \nonumber \]
\[ A_v = \frac{R_2}{R_1} +1 \label{6.30} \]
Equation \ref{6.30} is identical to the approximate gain Equation for an ordinary noninverting op amp stage. A closer look at the exact Equation (\ref{6.29}) reveals an important difference with the exact series-parallel expression examined in Chapter Three
\[ A_v = \frac{A_{ol}}{1+\beta A_{ol}} \nonumber \]
As you may recall, \(\beta\) is the feedback factor and determines the closed loop gain. To a first approximation, \(\beta A_{ol} \gg 1\), and thus, the series-parallel gain is ideally 1/\(\beta\). As frequency is raised, however, the value of Aol drops, and soon this approximation no longer holds. It is very important to note that the point at which the idealization ceases to be accurate is a function of \(\beta\). For higher closed-loop gains, \(\beta\) is smaller, and thus, the \(\beta A_{ol}\) product reaches unity at a lower frequency. It is this very interdependency that causes the gain/bandwidth trade-off. A close look at Equation \ref{6.29} shows no such interdependency. In this case, the denominator is not influenced by the feedback factor. In its place is the fixed resistor value \(R_2\). Normally, \(R_2\) is set by the manufacturer of the device, and is usually around 1 k\(\Omega\) to 2 k\(\Omega\) in size. Closed-loop gain is set by altering the value of \(R_1\). This means that the closed-loop upper-break frequency is not dependent on the closed-loop gain. This is the ideal case. In reality, secondary effects will cause some decrease of \(f_2\) with increasing \(A_v\). This effect is noticeable at medium to high gains, but is still considerably less than what an ordinary op amp would produce. For example, a jump in gain from 10 to 100 may drop \(f_2\) from 150 MHz to only 50 MHz, whereas an ordinary device would drop to 15 MHz.
The CLC1606 from Exar is one example of a current feedback amplifier. It boasts a slew rate of 3300 V/μs, a bandwidth of 1.3 GHz, and an output current capability of 120 mA. This makes it ideal for applications such as high-speed line drivers or video display drivers. The features and typical circuit are shown in Figure \(\PageIndex{2}\). Figure \(\PageIndex{3}\) shows the AC specifications. Note the small variation in \(f_2\) as the gain is changed from 1 to 2. In a “normal” op amp the bandwidth would be halved.

Figure \(\PageIndex{2}\): CLC1606 current feedback amplifier. Reprinted courtesy of Exar
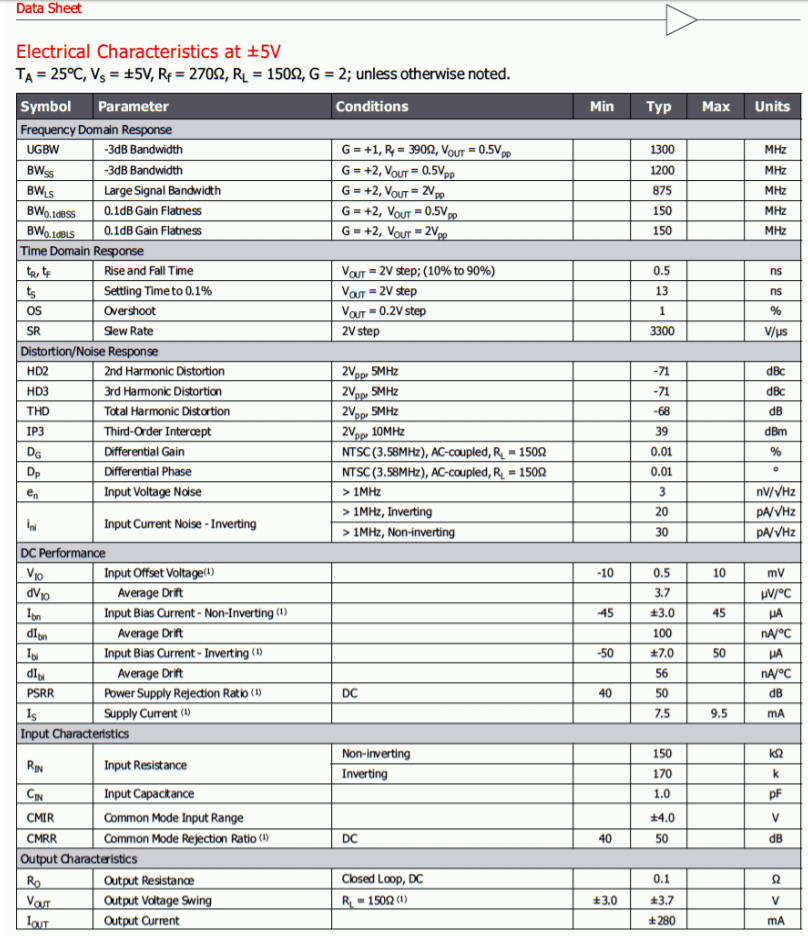
Figure \(\PageIndex{3}\): CLC1606 specifications. Reprinted courtesy of Exar
Example 6.7
Design a noninverting 100 MHz amplifier with a voltage gain of 14 dB, utilizing the CLC1606.
By design, the CLC1606 will meet our bandwidth requirement, as long as the desired gain is not excessive. A voltage gain of 14 dB translates to an ordinary gain of 5, which is not excessive. \(R_f\) is typically relatively low and assuming an \(R_f\) of 390 \(\Omega\), we find
\[ A_v = 1+ \frac{390}{R} \nonumber \]
\[ R_g = \frac{390}{A_v−1} \nonumber \]
\[ R_g = \frac{390}{5−1} \nonumber \]
\[ R_g = 97.5 \Omega \nonumber \]
As with any high-speed amplifier, care must be taken when laying out this circuit. Failure to do so may seriously degrade amplifier performance.


