4.8: Solving Linear Systems of Equations
- Page ID
- 10116
We are now equipped to set up systems of linear equations as matrix- vector equations so that they can be solved in a standard way on a computer. Suppose we want to solve the equations from Example 1 from "Linear Algebra: Introduction" for \(x_1\) and \(x_2\) using a computer. Recall that Equations 1 and 2 from Linear Algebra: Introduction are
\[x_{1}+x_{2}=85 \nonumber \]
\[\frac{x_{1}}{1.2}=\frac{x_{2}}{1.5-1.2} \nonumber \]
The first step is to arrange each equation with all references to \(x_1\) in the first column, all references to \(x_2\) in the second column, etc., and all constants on the right-hand side:
\(\begin{gathered}
x_{1}+x_{2}=85 \\
0.3 x_{1}-1.2 x_{2}=0
\end{gathered}\)
Then the equations can be converted to a single matrix-vector equation. The coefficients form a matrix, keeping their same relative positions, and the variables and constants each form a vector:
\[\left[\begin{array}{ll}
1 & 1 \\
0.3 & -1.2
\end{array}\right]\left[\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right]=\left[\begin{array}{l}
85 \\
0
\end{array}\right] \nonumber \]
Verify by the rules of matrix multiplication that the system of equations in 2 in equivalent to the matrix equation in 3.
Equation 3 is of the general form
\[A x=b \nonumber \]
where in this case
\[\mathrm{A}=\left[\begin{array}{ll}
1 & 1 \\
0.3 & -1.2
\end{array}\right], \mathrm{x}=\left[\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right], \mathrm{b}=\left[\begin{array}{l}
85 \\
0
\end{array}\right] . \nonumber \]
Given any \(A \in \mathscr{R}^{n \times n}\) and \(\mathrm{b} \in \mathscr{R}^{n}\), MATLAB can solve Equation 4 for \(x\) (as long as a solution exists). Key ideas in the solution process are the identity matrix and the inverse of a matrix.
When the matrix A is the 1×1 matrix \(a\), the vector \(x\) is the l-vector \(x\), and the vector \(b\) is the l-vector \(b\), then the matrix equation \(Ax=b\) becomes the scalar equation
\[a x=b \text { . } \nonumber \]
The scalar \(a^{−1}\) is the inverse of the scalar aa, so we may multiply on both sides of Equation 6 to obtain the result
\(a^{-1}(a x)=a^{-1} b\)
\[1 x=a^{-1} b \nonumber \]
We would like to generalize this simple idea to the matrix equation \(Ax=b\) so that we can find an inverse of the matrix \(A\), called \(A^{−1}\), and write
\(\mathrm{A}^{-1}(A x)=\mathrm{A}^{-1} \mathrm{~b}\)
\[I x=\mathrm{A}^{-1} \mathrm{~b} \nonumber \]
In this equation the matrix \(I\) is the identity matrix
\[\mathrm{I}=\left[\begin{array}{ccccc}
1 & 0 & 0 & \ldots & 0 \\
0 & 1 & 0 & \ldots & 0 \\
0 & 0 & 1 & \ldots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \ldots & 1
\end{array}\right] \nonumber \]
It is clear that the identity matrix \(I\) and the inverse of a matrix, \(A^{−1}\), play a key role in the solution of linear equations. Let's study them in more detail.
The Matrix Identity
When we multiply a scalar by 1, we get back that same scalar. For this reason, the number 1 is called the multiplicative identity element. This may seem trivial, but the generalization to matrices is more interesting. The question is, is there a matrix that, when it multiplies another matrix, does not change the other matrix? The answer is yes. The matrix is called the identity matrix and is denoted by \(I\). The identity matrix is always square, with whatever size is appropriate for the matrix multiplication. The identity matrix has 1's on its main diagonal and 0's everywhere else. For example,
\[I_{5}=\left[\begin{array}{lllll}
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 1
\end{array}\right] \text { . } \nonumber \]
The subscript 5 indicates the size. In terms of the unit coordinate vectors \(e_i\), we can also write the \(n×n\) identity matrix as
\[\mathrm{I}_{n}=\left[\begin{array}{cccc}
\mid & \mid & & 1 \\
\mathrm{e}_{1} & \mathrm{e}_{2} & \ldots & \mathrm{e}_{n} \\
\mid & \mid & & \mid
\end{array}\right] \nonumber \]
For any matrix \(A \in \mathscr{R}^{n \times n}\), we have
\[\mathrm{A}=\mathrm{I}_{n} \mathrm{~A} \nonumber \]
For \(p=1\), we obtain the following special form for any vector \(\mathrm{x} \in \mathscr{R}^{n}\):
\[\mathrm{x}=\mathrm{I}_{n} \mathrm{x} \nonumber \]
This last equation can be written as the sum
\[\mathrm{x}=\sum_{i=1}^{n} x_{i} \mathrm{e}_{i} \nonumber \]
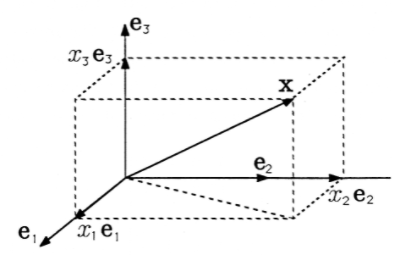
This is a special case of one of the results you proved in Exercise 3 from "Linear Algebra: Matrices". Figure 1 illustrates Equation 14 and shows how the vector \(x\) can be broken into component vectors \(x_ie_i\), each of which lies in the direction of one coordinate axis. The values of the \(x_i\)'s are the coordinates of \(x\), and their magnitudes are also the lengths of the component vectors.
Use Equation 13 and the rules for matrix multiplication to show that \(\mathrm{x} \in \mathscr{R}^{n}\) may also be written as
\[\mathrm{x}=\sum_{i=1}^{n}\left(\mathrm{x}, \mathrm{e}_{i}\right) \mathrm{e}_{i} \nonumber \]
This verifies Equation 11 from "Linear Algebra: Direction Cosines".
When the product of two numbers is 1 (the identity element), we say that they are inverses of each other, like 2 and 0.5. Likewise, we say that two square matrices are inverses of each other if their product is the identity matrix:
\[A B=\mathrm{I} \Leftrightarrow \mathrm{B}=\mathrm{A}^{-1} \nonumber \]
An interesting and useful result is implied by this definition. Take the first form of Equation 16 and multiply by \(B\) from the left:
\[\begin{align}
A B &=\mathrm{I} \nonumber \\
\Rightarrow B(A B)&=\mathrm{BI} \nonumber \\
\Rightarrow (B A) B&=\mathrm{B} \nonumber \\
\Rightarrow \quad B A&=\mathrm{I}
\end{align} \nonumber \]
We emphasize that the inference made in the last step here is only valid when \(B\) and \(A\) are square matrices. The result means that, even though matrix multiplication is not commutative in general, we have a special case where it is commutative. If \(A\) and \(B\) are inverses of each other, then
\[A B=\mathrm{BA}=\mathrm{I} \nonumber \]
Prove that the inverse of the 2x2 rotation matrix \(R(\theta)\) is \(R^T(\theta)\).
Matrices that are not square do not have inverses. In fact, not all square matrices have inverses. So it becomes an important issue to determine which matrices do have inverses. If a matrix has an inverse, the inverse is unique. If a square matrix has no inverse, it is called a singular matrix. The determinant of a square matrix is a scalar computed from the numbers in the matrix. It tells us whether a matrix will have an inverse or not. A matrix is singular if and only if its determinant is zero.1 In MATLAB, the notation det(A) is used to compute the determinant. Whenever the matrix A in Equation 4 is singular, it means one of two things about the system of equations represented: either the equations are inconsistent and there is no solution, or the equations are dependent and there are infinitely many solutions.
Solving
\(Ax = b\). Let's now study ways to solve the matrix equation \(Ax=b\). We will assume that a unique solution for \(x\) exists. Thus a unique matrix \(A^{−1}\) exists with the property \(A^{−1}A=I\). The trick is to find it. Here is one procedure.
For convenience, rewrite the matrix equation \(Ax =b\) as
\[[A b]\left[\begin{array}{l}
x \\
-1
\end{array}\right]=0 \nonumber \]
The matrix \([A b] \in \mathscr{R}^{n \mathrm{X}(n+1)}\) is called the augmented matrix for the system of equations. The augmented matrix may be viewed as a systematic way of writing all the information necessary to solve the equations.
The advantage of Equation 19 is that we may premultiply both sides by any matrix \(C_1\) (of compatible size), and the right-hand side remains zero (although this is equivalent to multiplying on both sides of Equation 4, which some may prefer). We can repeat this operation as often as we like with matrices \(C_2\), \(C_3\), etc. The general result is
\[\left[\mathrm{C}_{m} \cdots \mathrm{C}_{2} \mathrm{C}_{1} \mathrm{AC}_{m} \cdots \mathrm{C}_{2} \mathrm{C}_{1} \mathrm{~b}\right]\left[\begin{array}{l}
\mathrm{x} \\
-1
\end{array}\right]=0 \nonumber \]
Now suppose that we have found a sequence of matrices \(C_1\),..., \(C_m\) that transforms the matrix \(A\) to the identity matrix:
\(C_m \cdots C_2C_1A=I\). The augmented matrix equation in 20 simplifies to
\[\left[I \mathrm{C}_{m} \cdots \mathrm{C}_{2} \mathrm{C}_{1} \mathrm{~b}\right]\left[\begin{array}{l}
\mathrm{x} \\
-1
\end{array}\right]=0 \nonumber \]
which can be multiplied out to reveal that the solution for \(x\) is
\[\mathrm{x}=\mathrm{C}_{m} \cdots \mathrm{C}_{2} \mathrm{C}_{1} \mathrm{~b} \nonumber \]
The method may be summarized as follows:
- form the augmented matrix \([Ab]\) for the system;
- premultiply \([Ab]\) by a sequence of selected matrices \(C_i\), designed to take \(A\) to \(I\); and
- when \(A\) is transformed to \(I\), \(b\) will be transformed to \(x\), so the solution will appear as the last column of the transformed augmented matrix.
We may also conclude that the product of the matrices \(C_i\) must be the inverse of A since \(A^{−1}\) is the unique matrix for which \(A^{−1}A=I\). In solving for \(x\) by this method, we have found \(A^{−1}\) implicitly as the product \(C_m \cdots C_2C_1\).
Consider the equation
\(\left[\begin{array}{ll}
3 & 1 \\
2 & 4
\end{array}\right] \quad\left[\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right]=\left[\begin{array}{l}
6 \\
5
\end{array}\right]\)
\(Ax = b\)
The augmented matrix for this equation is
\(\left[\begin{array}{ll}
A & b
\end{array}\right]=\left[\begin{array}{lll}
3 & 1 & 6 \\
2 & 4 & 5
\end{array}\right]\)
Now if we could add −2/3 times the first row to the second row, we would get 0 in the lower left corner. This is the first step in transforming A to the identity I. We can accomplish this row operation with the matrix
\(\mathrm{C}_{1}=\left[\begin{array}{ll}
1 & 0 \\
-2 / 3 & 1
\end{array}\right]\)
\(\mathrm{C}_{1}\left[\begin{array}{ll}
A & b
\end{array}\right]=\left[\begin{array}{lll}
3 & 1 & 6 \\
0 & 10 / 3 & 1
\end{array}\right]\)
Now adding −3/10 times the new second row to the first row will introduce 0 in the (1,2) position, bringing us closer still to the identity. Thus
\(C_{2}=\left[\begin{array}{ll}
1 & -3 / 10 \\
0 & 1
\end{array}\right]\)
\(\mathrm{C}_{2} \mathrm{C}_{1} \quad\left[\begin{array}{lll}
A & b
\end{array}\right]=\left[\begin{array}{lll}
3 & 0 & 57 / 10 \\
0 & 10 / 3 & 1
\end{array}\right]\)
We now complete the transformation to identity by normalizing each row to get the needed l's:
\(\mathrm{C}_{3}=\left[\begin{array}{ll}
1 / 3 & 0 \\
0 & 3 / 10
\end{array}\right]\)
\(\mathrm{C}_{3} \mathrm{C}_{2} \mathrm{C}_{1} \quad\left[\begin{array}{ll}
A & \mathrm{~b}
\end{array}\right]=\left[\begin{array}{lll}
1 & 0 & 19 / 10 \\
0 & 1 & 3 / 10
\end{array}\right]\)
According to the last column, the solution is
\(\mathrm{x}=\left[\begin{array}{l}
19 / 10 \\
3 / 10
\end{array}\right]\)
We note in passing that the inverse of \(A\) is the product of the C′s, so
\(\begin{aligned}
\mathrm{A}^{-1}=\mathrm{C}_{3} \mathrm{C}_{2} \mathrm{C}_{1} &= \qquad \left[\begin{array}{ll}
1 / 3 & 0 \\
0 & 3 / 10
\end{array}\right]\left[\begin{array}{ll}
1 & -3 / 10 \\
0 & 1
\end{array}\right]\left[\begin{array}{ll}
1 & 0 \\
-2 / 3 & 1
\end{array}\right] \\
&=\left[\begin{array}{ll}
1 / 3 & -1 / 10 \\
0 & 3 / 10
\end{array}\right]\left[\begin{array}{ll}
1 & 0 \\
-2 / 3 & 1
\end{array}\right]=\left[\begin{array}{ll}
2 / 5 & -1 / 10 \\
-1 / 5 & 3 / 10
\end{array}\right] .
\end{aligned}\)
The method we have just used, combined with a particular way of choosing the \(C_i\) matrices, is called Gauss elimination. Gauss elimination requires less computation than finding the inverse of A because only the effect of \(A^{−1}\) on the specific vector \(b\) is computed. MATLAB can solve for \(x\) by either method, as shown in Demo 4.2. For hand computations, we suggest choosing the \(C_i\) matrices so that \(C_1\) produces O′s everywhere below the diagonal in the first column, \(C_2\) produces O′s below the diagonal in the second column, and so on up to \(C_{n−1}\). Then \(C_n\) produces O′s above the diagonal in the \(n^{th}\) column, \(C_{n+1}\) produces O′s above the diagonal in column \(n−1\), etc. The last one, \(C_{2n−1}\), normalizes the diagonal elements to l's. We have assumed for simplicity that no O′s on the diagonal will be encountered in hand computations.
Check that \(A^{−1}A=I\) in Example 1.
Augment Equation 3 as in Equation 19 and use the technique of Gauss elimination to solve for \(x\).
Demo 1 (MATLAB)
From the command level of MATLAB, solve the matrix equation of Example 1 from "Linear Algebra: Introduction" by typing
>> A = [1 1; 0.3 - 1.2] >> b = [85;0]
You have entered the matrices \(A\) and \(b\), which describe the problem. You can now solve for \(x\) by finding the inverse of \(A\) and multiplying \(b\):
>> x = inv(A) * b
In this example the inverse is computed quickly because \(A\) is a small matrix. For a large (say, 30×30) matrix, the answer would take longer to compute, and the more efficient method of Gauss elimination would reduce waiting time. You can use Gauss elimination in MATLAB by typing
>> x = A \ b
You should get the same answer. Now type the MATLAB code required to compute \(Ax\) and to show \(Ax−b=0\).
(MATLAB) Write the following system of equations as \(Ax=b\) and solve using MATLAB:
\(\begin{gathered}
3\left(x_{1}-x_{3}\right)+2\left(x_{2}-1\right)-6=x_{3} \\
4 x_{3}=7 x_{2}-5 \\
6\left(x_{1}+x_{2}+2\right)=x_{3}+1 .
\end{gathered}\)
Footnotes
- It is not important now to understand how the determinant is defined and computed from the elements of a matrix. In your more advanced courses you will study the determinant in some detail.


