6.4: Moving Averages
- Page ID
- 9985
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Moving averages are generalizations of weighted averages. They are designed to “run along an input sequence, computing weighted averages as they go.” A typical moving average over \(N\) inputs takes the form
\[\begin{align}
x_{n} &=\qquad \qquad \qquad \sum_{k=0}^{N-1} w_{k} u_{n-k} \nonumber\\
&=w_{0} u_{n}+w_{1} u_{n-1}+\cdots+w_{N-1} u_{n-(N-1)}
\end{align} \nonumber \]
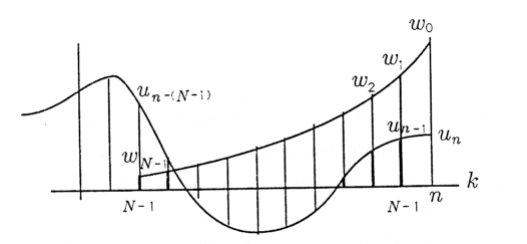
The most current input, \(u_n\), is weighted by \(w_0\); the next most current input, \(u_{n-1}\), is weighted by \(w_1\) ; and so on. This weighting is illustrated in Figure 1. The sequence of weights, \(w_0\) through \(w_{N-1}\), is called a “window,” a “weighting sequence,” or a “filter.” In the example illustrated in Figure 6.8, the current value \(u_n\) is weighted more heavily than the least current value. This is typical (but not essential) because we usually want \(x_n\) to reflect more of the recent past than the distant past.
When the weights \(w_{0}, w_{1}, \ldots, w_{N-1}\) are all equal to \(\frac{1}{N}\), then the moving average \(x_n\) is a “simple moving average”:
\[x_{n}=\frac{1}{N}\left[u_{n}+u_{n-1}+\cdots+u_{N-1}\right] . \nonumber \]
This is the same as the simple average, but now the simple average moves along the sequence of inputs, averaging the \(N\) most current values.
Evaluate the moving average \(x_{n}=\sum_{k=0}^{N-1} \frac{1}{N} u_{n-k}\) for the inputs
- \(u_{n}= \begin{cases}0, & n<0 \\ u, & n \geq 0\end{cases}\)
- \(u_{n}= \begin{cases}0, & n \leq 0 \\ n, & n>0\end{cases}\)
Interpret your findings.
Evaluate the simple moving average \(x_{n}=\sum_{k=0}^{N-1} \frac{1}{N} u_{n-k}\) when \(u_n\) is the sequence
\(u_{n}= \begin{cases}0, & n<0 \\ a^{n}, & n \geq 0\end{cases}\)
Interpret your result.
When the weights \(w_n\) equal \(w_0a^n\) for \(n=0,1,...,N−1\), then the moving average \(x_n\) takes the form
\[x_{n}=w_{0} \sum_{k=0}^{N-1} a^{k} u_{n-k} . \nonumber \]
When \(a < 1\), then \(u_n\) is weighted more heavily than \(u_{n−(N−1)}\); when \(a>1\), \(u_{n−(N−1)}\) is weighted more heavily than \(u_n\); when \(a=1\), \(u_n\) is weighted the same as \(u_{n−(N−1)}\).
Evaluate \(w_0\) so that the exponential weighting sequence \(w_{n}=w_{0} a^{n}(n=0,1, \ldots, N-1)\) is a valid window (i.e., \(\sum_{n=0}^{N-1} w_{n}=1\)).
Compute the moving average \(x_{n}=\sum_{k=0}^{N-1} w_{0} a^{k} u_{n-k}\) when the input sequence \(u_n\) is
\(u_{n}= \begin{cases}b^{n}, & n \geq 0 \\ 0, & n<0\end{cases}\)
What happens when \(b=a?\) Can you explain this?