Knowing the polynomial algebra underlying the DFT enables us to derive the Cooley-Tukey FFT algebraically. This means that instead of manipulating the DFT definition, we manipulate the polynomial algebra C[s]/(sN-1)C[s]/(sN-1)" role="presentation" style="position:relative;" tabindex="0">\(\mathbb{C}[s]/(s^N-1)\). The basic idea is intuitive. We showed that the DFT is the matrix representation of the complete decomposition equation.The Cooley-Tukey FFT is now derived by performing this decomposition in steps as shown in Fig. 7.3.1. Each step yields a sparse matrix; hence, the DFTNDFTN" role="presentation" style="position:relative;" tabindex="0">\(\text{DFT}_N\) is factorized into a product of sparse matrices, which will be the matrix representation of the Cooley-Tukey FFT.
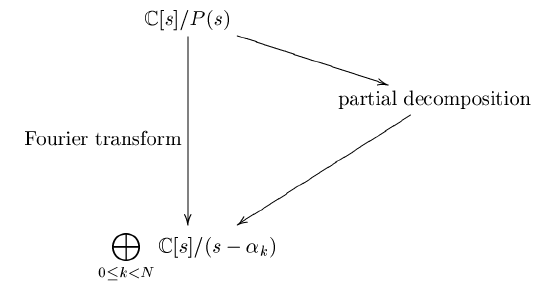
Fig. 7.3.1 Basic idea behind the algebraic derivation of Cooley-Tukey type algorithms
This stepwise decomposition can be formulated generically for polynomial transforms. Here, we consider only the DFT. We first introduce the matrix notation we will use and in particular the Kronecker product formalism that became mainstream for FFTs. Then we first derive the radix-2 FFT using a factorization of sN-1sN-1" role="presentation" style="position:relative;" tabindex="0">\(s^N-1\). Subsequently, we obtain the general-radix FFT using a decomposition of sN-1sN-1" role="presentation" style="position:relative;" tabindex="0">sN-1sN-1" role="presentation" style="position:relative;" tabindex="0">\(s^N-1\).
Matrix Notation
We denote the N×NN×N" role="presentation" style="position:relative;" tabindex="0">\(N\times N\) identity matrix with ININ" role="presentation" style="position:relative;" tabindex="0">\(I_N\), and diagonal matrices with
\[\text{diag}_{0\leq k< N}(\gamma _k)=\begin{bmatrix} \gamma _0 & & & & \\ & . & & & \\ & & . & & \\ & & & . & \\ & & & & \gamma _{N-1} \end{bmatrix} \nonumber \]
The N×NN×N" role="presentation" style="position:relative;" tabindex="0">\(N\times N\) stride permutation matrix is defined for N=KMN=KM" role="presentation" style="position:relative;" tabindex="0">\(N=KM\) by the permutation
\[L_{M}^{N}=iK+j\mapsto jM+i \nonumber \]
for \(0\leq i< K,\; 0\leq j< M\). This definition shows that LMNLMN" role="presentation" style="position:relative;" tabindex="0">\(L_{M}^{N}\) transposes a \(K\times M\) matrix stored in row-major order. Alternatively, we can write
\[L_{M}^{N}:i\mapsto \text{iM}\: \text{mod}\: N-1,\: \text{for}\: 0\leq i< N-1,\: N-1\mapsto N-1 \nonumber \]
For example (·means 0),
\[L_{2}^{6}=\begin{bmatrix} 1 & . & . & . & . & .\\ . & . & 1 & . & . & .\\ . & . & . & . & 1 & .\\ . & 1 & . & . & . & .\\ . & . & . & 1 & . & .\\ . & . & . & . & . & 1 \end{bmatrix} \nonumber \]
\(L_{N/2}^{N}\) is sometimes called the perfect shuffle.
Further, we use matrix operators; namely the direct sum
\[A\oplus B=\begin{bmatrix} A & \\ & B \end{bmatrix} \nonumber \]
and the Kronecker or tensor product
\[A\otimes B=\left [ a_{k,l}B \right ]_{k,l},\: \: \text{for}\: A=[a_{k,l}] \nonumber \]
In particular,
\[I_n\otimes A=A\oplus ...\oplus A=\begin{bmatrix} A & & & & \\ & . & & & \\ & & . & & \\ & & & . & \\ & & & & A \end{bmatrix} \nonumber \]
is block-diagonal.
We may also construct a larger matrix as a matrix of matrices, e.g.,
\[\begin{bmatrix} A & B\\ B & A \end{bmatrix} \nonumber \]
If an algorithm for a transform is given as a product of sparse matrices built from the constructs above, then an algorithm for the transpose or inverse of the transform can be readily derived using mathematical properties including
\[(AB)^T=B^TA^T,\; \; \; (AB)^{-1}=B^{-1}A^{-1} \nonumber \]
\[(A\oplus B)^T=A^T\oplus B^T,\; \; \; (A\oplus B)^{-1}=A^{-1}\oplus B^{-1} \nonumber \]
\[(A\otimes B)^T=A^T\otimes B^T,\; \; \; (A\otimes B)^{-1}=A^{-1}\otimes B^{-1} \nonumber \]
Permutation matrices are orthogonal, i.e., \(P^T=P^{-1}\). The transposition or inversion of diagonal matrices is obvious.
Radix-2 FFT
The DFT decomposes \(\mathfrak{A}=\mathbb{C}[s]/(s^N-1)\) with basis b=(1,s,⋯,sN-1)b=(1,s,⋯,sN-1)" role="presentation" style="position:relative;" tabindex="0">\(b=1,s,...,s^{N-1}\) as shown in the equation. We assume N=2MN=2M" role="presentation" style="position:relative;" tabindex="0">\(N=2M\). Then
\[s^{2M}-1=(s^M-1)(s^M+1) \nonumber \]
factors and we can apply the CRT in the following steps:
\[\mathbb{C}[s]/(s^N-1) \nonumber \]
\[\rightarrow \mathbb{C}[s]/(s^M-1)\oplus \mathbb{C}[s]/(s^M+1) \nonumber \]
\[\rightarrow \underset{0\leq i< M}{\oplus }\mathbb{C}[s]/(x-W_{N}^{2i})\oplus \underset{0\leq i< M}{\oplus }\mathbb{C}[s]/(x-W_{M}^{2i+1}) \nonumber \]
\[\rightarrow \underset{0\leq i< N}{\oplus }\mathbb{C}[s]/(x-W_{N}^{i}) \nonumber \]
As bases in the smaller algebras \(\mathbb{C}[s]/(s^M-1)\) and \(\mathbb{C}[s]/(s^M+1)\), we choose \(c=d=1,s,...,s^{M-1}\). The derivation of an algorithm for DFTNDFTN" role="presentation" style="position:relative;" tabindex="0">\(\text{DFT}_N\) based on the equations is now completely mechanical by reading off the matrix for each of the three decomposition steps. The product of these matrices is equal to the DFTNDFTN" role="presentation" style="position:relative;" tabindex="0">\(\text{DFT}_N\).
First, we derive the base change matrix BB" role="presentation" style="position:relative;" tabindex="0">\(B\) corresponding to the equation. To do so, we have to express the base elements sn∈bsn∈b" role="presentation" style="position:relative;" tabindex="0">\(s^n\in b\) in the basis \(c\cup d\); the coordinate vectors are the columns of BB" role="presentation" style="position:relative;" tabindex="0">\(B\). For \(0\leq n< M,\: s^n\) is actually contained in BB" role="presentation" style="position:relative;" tabindex="0">\(c\) and BB" role="presentation" style="position:relative;" tabindex="0">\(d\)cc" role="presentation" style="position:relative;" tabindex="0">, so the first BB" role="presentation" style="position:relative;" tabindex="0">\(M\)MM" role="presentation" style="position:relative;" tabindex="0"> columns of BB" role="presentation" style="position:relative;" tabindex="0">\(B\) are
\[B=\begin{bmatrix} I_M & \ast \\ I_M & \ast \end{bmatrix} \nonumber \]
where the entries \(\ast\) are determined next. For the base elements \(s^{M+n},\: 0\leq n< M\), we have
\[s^{M+n}=s^n\: \text{mod}\: (s^M-1) \nonumber \]
\[s^{M+n}=-s^n\: \text{mod}\: (s^M+1) \nonumber \]
which yields the final result
\[B=\begin{bmatrix} I_M & I_M\\ I_M & -I_M \end{bmatrix}=\text{DFT}_2\otimes I_M \nonumber \]
Next, we consider step equation. \(\mathbb{C}[s]/(s^M-1)\) is decomposed by DFTMDFTM" role="presentation" style="position:relative;" tabindex="0">\(\text{DFT}_M\) and \(\mathbb{C}[s]/(s^M+1)\) by \(\text{DFT}-3_{M}\) in the equation.
Finally, the permutation in step in the equation is the perfect shuffle LMNLMN" role="presentation" style="position:relative;" tabindex="0">\(L_{M}^{N}\), which interleaves the even and odd spectral components (even and odd exponents of WNWN" role="presentation" style="position:relative;" tabindex="0">\(W_N\)).
The final algorithm obtained is
\[\text{DFT}_{2M}=L_{M}^{N}(\text{DFT}_{M}\oplus \text{DFT}-3_{M})(\text{DFT}_{2}\otimes I_M) \nonumber \]
\[\text{DFT}_{2M}=L_{M}^{N}(I_2\otimes \text{DFT}_{M})(I_M\oplus D_M)(\text{DFT}_{2}\otimes I_M) \nonumber \]
The last expression is the radix-\(2\) decimation-in-frequency Cooley-Tukey FFT. The corresponding decimation-in-time version is obtained by transposition using the equation and the symmetry of the DFT:
\[\text{DFT}_{2M}=(\text{DFT}_{2}\otimes I_M))(I_M\oplus D_M)(I_2\otimes \text{DFT}_{M})L_{2}^{N} \nonumber \]
The entries of the diagonal matrix IM⊕DMIM⊕DM" role="presentation" style="position:relative;" tabindex="0">\(I_M\oplus D_M\) are commonly called twiddle factors.
General-radix FFT
To algebraically derive the general-radix FFT, we use the decomposition property of sN-1sN-1" role="presentation" style="position:relative;" tabindex="0">\(s^N-1\). Namely, if N=KMN=KM" role="presentation" style="position:relative;" tabindex="0">\(N=KM\) then
\[s^N-1=(s^M)^K-1 \nonumber \]
Decomposition means that the polynomial is written as the composition of two polynomials: here, \(s^M\) is inserted into \(s^K-1\). Note that this is a special property: most polynomials do not decompose.
Based on this polynomial decomposition, we obtain the following stepwise decomposition of \(\mathbb{C}[s]/(s^N-1)\), which is more general than the previous one in the equations. The basic idea is to first decompose with respect to the outer polynomial tK-1tK-1" role="presentation" style="position:relative;" tabindex="0">\(t^K-1,\: t=s^M\) and then completely.
\[\mathbb{C}[s]/(s^N-1)=\mathbb{C}[x]/\left ( (s^M)^K-1 \right ) \nonumber \]
\[\rightarrow \underset{0\leq i< K}{\oplus }\mathbb{C}[s]/(s^M-W_{K}^{i}) \nonumber \]
\[\rightarrow \underset{0\leq i< K}{\oplus }\underset{0\leq j< M}{\oplus }\mathbb{C}[s]/(x-W_{N}^{jK+i}) \nonumber \]
\[\rightarrow \underset{0\leq i< N}{\oplus }\mathbb{C}[s]/(x-W_{N}^{i}) \nonumber \]
As bases in the smaller algebras \(\mathbb{C}[s]/(s^M-W_{K}^{i})\) we choose ci=(1,s,⋯,sM-1)ci=(1,s,⋯,sM-1)" role="presentation" style="position:relative;" tabindex="0">\(c_i=1,s,...,s^{M-1}\). As before, the derivation is completely mechanical from here: only the three matrices corresponding to the equations have to be read off.
The first decomposition step requires us to compute \(s^n\: \text{mod}\: \left ( s^M-W_{K}^{i} \right ),\: 0\leq n< N\). To do so, we decompose the index \(n\) as \(n=lM+m\) and compute
\[s^n=s^{lM+m}=(s^M)^ls^m\equiv W_{k}^{lm}s^m\: \text{mod}\: (s^M-W_{K}^{i}) \nonumber \]
This shows that the matrix for is given by: \(\text{DFT}_K\otimes I_M\)
In step equation, each \(\mathbb{C}[s]/(s^M-W_{K}^{i})\) is completely decomposed by its polynomial transform
\[\text{DFT}_M(i,K)=\text{DFT}_{M}.\text{diag}_{0\leq i< M}(W_{N}^{ij}) \nonumber \]
At this point, \(\mathbb{C}[s]/(s^N-1)\) is completely decomposed, but the spectrum is ordered according to jK+ijK+i" role="presentation" style="position:relative;" tabindex="0">\(jK+i,\: 0\leq i< M,\: 0\leq j< K,\) (\(j\) runs faster). The desired order is iM+jiM+j" role="presentation" style="position:relative;" tabindex="0">\(iM+j\).
Thus, in step equation, we need to apply the permutation \(jK+i\mapsto iM+j\), which is exactly the stride permutation LMNLMN" role="presentation" style="position:relative;" tabindex="0">\(L_{M}^{N}\) in the equation.
In summary, we obtain the Cooley-Tukey decimation-in-frequency FFT with arbitrary radix:
\[L_{M}^{N}\left ( \underset{0\leq i< K}{\oplus }\text{DFT}_M .\text{diag}_{0\leq i< M}\left ( W_{N}^{ij}\right )\right )(\text{DFT}_k\otimes I_M) \nonumber \]
\[=L_{M}^{N}(I_K{\otimes }\text{DFT}_M )T_{M}^{N}(\text{DFT}_k\otimes I_M) \nonumber \]
The matrix TMNTMN" role="presentation" style="position:relative;" tabindex="0">\(T_{M}^{N}\) is diagonal and usually called the twiddle matrix. Transposition using the equation yields the corresponding decimation-in-time version:
\[(\text{DFT}_k\otimes I_M)T_{M}^{N}(I_K{\otimes }\text{DFT}_M )L_{K}^{N} \nonumber \]



