3.6: Translational Spring and Viscous Damper (Dashpot)

Last updated
Save as PDF

Page ID: 7640

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The linear translation spring was introduced in Section 1.9 as the mechanical element connecting a mass to a rigid wall; for that simple case, the end of the spring attached to the wall was stationary. Now, let us consider the more general case in which both ends of the spring can move, as indicated in Figure \(\PageIndex{1}\). The force \(f_{x}(t)\) required to deform the spring by the amount \(x_{b}(t)-x_{a}(t)\), relative to the undeformed length of the spring, is proportional to the deformation. With the constant of proportionality denoted as \(k\), the more general spring law is

\[f_{x}(t)=k\left[x_{b}(t)-x_{a}(t)\right]\label{eqn:3.18} \]

The standard sign convention defines stretching of the spring as positive, \(x_{b}-x_{a}\) > 0, corresponding to tensile force, \(f_{x}(t)>0\); accordingly, compression is negative in the standard convention. Equation \(\ref{eqn:3.18}\) clearly accommodates both tension and compression of the spring. Occasionally, however, it is convenient to define compression as positive, as is illustrated in Example 3-4 in the next section.

Figure \(\PageIndex{1}\): Ideal linear spring with stiffness constant \(k\)

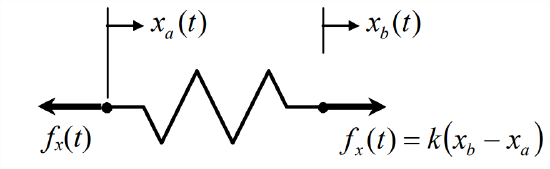
With the spring end forces equal and opposite as shown in Figure \(\PageIndex{1}\), we have neglected the inertial force of the spring. Inertial forces are terms such as \(m \times a\), mass times acceleration, in Newton’s 2^nd law. In this case, the inertial force of the spring is \(m_{s} \times \ddot{x}_{s}\), in which \(m_s\) is the mass of the spring, and \(\ddot{x}_{s}\) is acceleration of the spring’s center of mass. So neglecting inertial forces means we assume they are negligibly small in comparison with the force of Equation \(\ref{eqn:3.18}\). Notice that this does not strictly mean we are neglecting the mass, because even a tiny mass, when multiplied by a large acceleration, can produce a non-negligible inertial force. It is common to neglect the inertial forces of springs, but we should remember when doing so that we are really assuming both the inertias are small and the accelerations are sufficiently slow.

A dashpot (mechanical viscous damper) is a discrete component that resists translational velocity. An idealized linear, viscous damper is represented graphically by a piston-cylinder assembly, Figure \(\PageIndex{1}\). This device opposes relative velocity between piston and cylinder. With the forces on the dashpot defined to be positive in tension, as shown on Figure \(\PageIndex{1}\), the linear damping law is

\[f_{x}(t)=c\left[\dot{x}_{c}(t)-\dot{x}_{p}(t)\right]\label{eqn:3.19} \]

in which \(c\) is the damping constant. The damping constant plays the same role for a dashpot here that it plays in Chapter 1 [Figure 1.3.1 and Equation 1.3.4] for a block sliding on a viscous liquid film. If we were to define the forces to be positive in compression, then we would have to reverse the signs in the damping law, Equation \(\ref{eqn:3.19}\); it is sometimes appropriate to do so, as in Example 3-4 in the next section.

Figure \(\PageIndex{2}\): Ideal linear, viscous dashpot with damping constant \(c\)

With the cylinder and piston forces equal and opposite as shown in Figure \(\PageIndex{2}\), we have neglected the inertial forces of the cylinder and piston. It is common to neglect the inertial forces of dashpots, but we should remember when doing so that we are really assuming that both the inertias are small and the accelerations are sufficiently slow. On the other hand, in Example 3-4 of the next section, inertial forces of a piston-cylinder assembly are not neglected.

The idealized dashpot model of Figure \(\PageIndex{2}\) and Equation \(\ref{eqn:3.19}\) is convenient for linear mathematical analysis because of its simplicity. It is assumed to resist motion between piston and cylinder by means of the drag force produced by a viscous fluid boundary layer between the two solid objects. We can use the simple dashpot to model approximately real devices such as door dampers and shock absorbers. However, it is not a precise model for most real damping devices. In most real translational dampers, a piston forces fluid through an orifice within a cylinder, and this generates a major portion of the resisting force. Unfortunately for the purposes of linear mathematical analysis, the resisting force is a complex and highly nonlinear function of the relative motion between piston and cylinder.