7.1: Standard Form for Undamped Second Order Systems and Natural Frequency
- Page ID
- 7663
For the mass-damper-spring (\(m\)-\(c\)-\(k\)) system of Figure \(\PageIndex{1}\), the ODE of motion Equation 3.7.1 derived from Newton’s 2nd law, with use of the FBD in Figure 3.7.1, is
\[m \ddot{x}+c \dot{x}+k x=f_{x}(t)\label{eqn:7.1} \]
If we neglect damping by setting \(c \dot{x}= 0\) in Equation \(\ref{eqn:7.1}\), then we have an ideal (not real) undamped mass-spring (\(m\)-\(k\)) system. This undamped passive system is not fully realistic because every passive physical system is afflicted with some type and degree of energy dissipation, albeit very small in some systems1. Nevertheless, it is useful to study the undamped system because it reveals some important fundamental characteristics of 2nd order systems. From Equation \(\ref{eqn:7.1}\), the ODE for the \(m\)-\(k\) system is:
\[m \ddot{x}+k x=f_{x}(t) \Rightarrow \ddot{x}+\frac{k}{m} x=\frac{1}{m} f_{x}(t)=\frac{k}{m} \frac{f_{x}(t)}{k}\label{eqn:7.2} \]

Let us use Equation \(\ref{eqn:7.2}\) to develop the standard form that will apply for undamped 2nd order systems more generally. First, we define algebraically the natural frequency of undamped vibration as the positive square root of the quotient of the stiffness and mass values (both of which are positive in most passive systems):
\[\omega_{n} \equiv \sqrt{\frac{k}{m}}\label{eqn:7.3} \]
The natural frequency is very important physically: it is shown in the next section that an undamped 2nd order system tends to vibrate (oscillate, pulsate, shake, quiver, …) periodically at circular frequency \(\omega_{n}\) radians per second. Next, we define the standard input quantity
\[u(t) \equiv \frac{1}{k} f_{x}(t)\label{eqn:7.4} \]
So now we define \(x(t)\) as representing any appropriate output quantity (not necessarily just position as in Figure \(\PageIndex{1}\)), and we re-write Equation \(\ref{eqn:7.2}\) in standard form ( standard in this book, at least, and mostly standard in engineering literature):
\[\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\label{eqn:7.5} \]
From Equation \(\ref{eqn:7.5}\) we see that input \(u(t)\) has exactly the same physical dimensions as output \(x(t)\). In fact, we can identify \(u(t)\) as being the pseudo-static output, \(x_{p s}(t)\); that is, if \(x(t)\) varies slowly enough that \(\ddot{x}\) is negligible in comparison with \(\omega_{n}^{2} x\), then ODE Equation \(\ref{eqn:7.5}\) reduces to a simple algebraic equation, \(\omega_{n}^{2} x \approx \omega_{n}^{2} u(t)\), the solution of which is the pseudo-static response, \(x(t)=u(t) \equiv x_{p s}(t)\). This response is called pseudo-static because it is not necessarily static (constant over time), but it varies slowly enough that the second derivative of response is negligible.
Example \(\PageIndex{1}\)
You have probably seen the pendulum of a grandfather clock. The ideal simple pendulum is very similar: there is a bob of mass \(m\) attached to the lower end of a rod of length \(\ell\), the upper end of the rod being supported at frictionless hinge \(H\). We assume the rod to be rigid and to have negligible inertial moment. The pendulum hangs downward and swings side-to-side with angle \(\theta(t)\) in the plane of the paper, subject to the acceleration of gravity, \(g\). For completeness, we include an agent that can impose onto the pendulum an arbitrary applied moment \(M(t)\) about \(H\). Because we neglect the inertia of the rod, the rotational inertia of the pendulum about \(H\) is \(J=m \ell^{2}\).
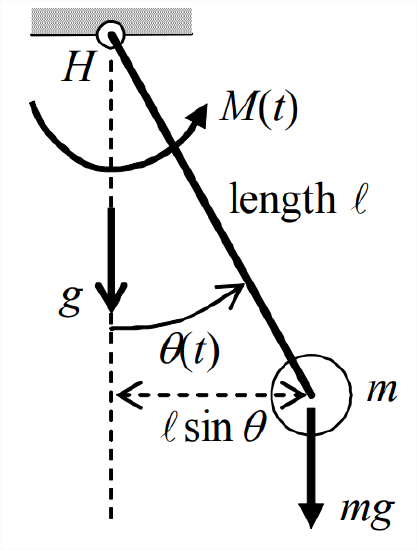
Newton’s 2nd law for rotation about \(H\) is
\[\Sigma(\text { all applied moments about } H)=J \times\text{ rotational acceleration }=m \ell^{2} \ddot{\theta} \nonumber \]
\[\Rightarrow \quad M(t)-m g \times \ell \sin \theta=m \ell^{2} \ddot{\theta} \Rightarrow m \ell^{2} \ddot{\theta}+m g \ell \sin \theta=M(t) \nonumber \]
Due to the \(\sin\theta\) term, the exact ODE is nonlinear. However, let us consider only small rotational angles, \(|\theta|<\approx 10^{\circ}\), for which \(\sin \theta \cong \theta\) in radians. This restriction linearizes the ODE:
\[m \ell^{2} \ddot{\theta}+m g \ell \theta=M(t) \Rightarrow \ddot{\theta}+\frac{g}{\ell} \theta=\frac{g}{\ell} \frac{M(t)}{m g \ell} \Rightarrow \ddot{\theta}+\omega_{n}^{2} \theta=\omega_{n}^{2} u(t) \nonumber \]
In the standardized form of the linearized ODE, the natural frequency is \(\omega_{n}=\sqrt{g / \ell}\), and the standard input quantity (also the pseudo-static response) is \(u(t)=\theta_{p s}(t)=M(t) / m g \ell\). For the pendulum at small rotational angles, the term \(m g \ell \theta\) is the restoring moment that opposes motion from the unforced static equilibrium position, \(\theta\) = 0; essentially, gravity plays the role of a rotation spring. See homework Problem 7.4 for another interesting pendulous rotational system, a balloon carrying a basket.


