2.2: Linear Time Invariant Systems
- Page ID
- 22845
Introduction
Linearity and time invariance are two system properties that greatly simplify the study of systems that exhibit them. In our study of signals and systems, we will be especially interested in systems that demonstrate both of these properties, which together allow the use of some of the most powerful tools of signal processing.
Linear Time Invariant Systems
Linear Systems
If a system is linear, this means that when an input to a given system is scaled by a value, the output of the system is scaled by the same amount.
Linear Scaling
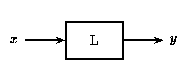 (a)
(a)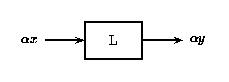 (b)
(b)
Figure \(\PageIndex{1}\)
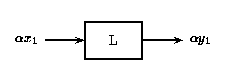
In Figure \(\PageIndex{1}\)(a) above, an input \(x\) to the linear system \(L\) gives the output \(y\). If \(x\) is scaled by a value \(\alpha\) and passed through this same system, as in Figure \(\PageIndex{1}\)(b), the output will also be scaled by \(\alpha\).
A linear system also obeys the principle of superposition. This means that if two inputs are added together and passed through a linear system, the output will be the sum of the individual inputs' outputs.
 (a)
(a) (b)
(b)
Figure \(\PageIndex{2}\)
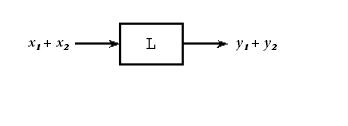
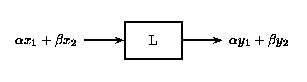
That is, if Figure \(\PageIndex{2}\) is true, then Figure \(\PageIndex{3}\) is also true for a linear system. The scaling property mentioned above still holds in conjunction with the superposition principle. Therefore, if the inputs x and y are scaled by factors \(\alpha\) and \(\beta\), respectively, then the sum of these scaled inputs will give the sum of the individual scaled outputs:
 (a)
(a)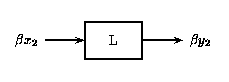 (b)
(b)
Figure \(\PageIndex{4}\)
Example \(\PageIndex{1}\)
Consider the system \(H_1\) in which
\[H_{1}(f(t))=t f(t) \nonumber \]
for all signals \(f\). Given any two signals \(f\), \(g\) and scalars \(a\), \(b\)
\[\left.H_{1}(a f(t)+b g(t))\right)=t(a f(t)+b g(t))=atf(t)+b t g(t)=a H_{1}(f(t))+b H_{1}(g(t)) \nonumber \]
for all real \(t\). Thus, \(H_1\) is a linear system.
Example \(\PageIndex{2}\)
Consider the system \(H_2\) in which
\[H_{2}(f(t))=(f(t))^{2} \nonumber \]
for all signals \(f\). Because
\[H_{2}(2 t)=4 t^{2} \neq 2 t^{2}=2 H_{2}(t) \nonumber \]
for nonzero \(t\), \(H_2\) is not a linear system.
Time Invariant Systems
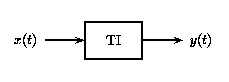
A time-invariant system has the property that a certain input will always give the same output (up to timing), without regard to when the input was applied to the system.
Time-Invariant Systems
 (a)
(a)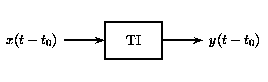 (b)
(b)In this figure, \(x(t)\) and \(x(t−t_0)\) are passed through the system TI. Because the system TI is time-invariant, the inputs \(x(t)\) and \(x(t−t_0)\) produce the same output. The only difference is that the output due to \(x(t−t_0)\) is shifted by a time \(t_0\).
Whether a system is time-invariant or time-varying can be seen in the differential equation (or difference equation) describing it. Time-invariant systems are modeled with constant coefficient equations. A constant coefficient differential (or difference) equation means that the parameters of the system are not changing over time and an input now will give the same result as the same input later.
Example \(\PageIndex{3}\)
Consider the system \(H_1\) in which
\[H_{1}(f(t))=t f(t) \nonumber \]
for all signals \(f\). Because
\[S_{T}\left(H_{1}(f(t))\right)=S_{T}(t f(t))=(t-T) f(t-T) \neq t f(t-T)=H_{1}(f(t-T))=H_{1}\left(S_{T}(f(t))\right) \nonumber \]
for nonzero \(T\), \(H_1\) is not a time invariant system.
Example \(\PageIndex{4}\)
Consider the system \(H_2\) in which
\[H_{2}(f(t))=(f(t))^{2} \nonumber \]
for all signals \(f\). For all real \(T\) and signals \(f\),
\[S_{T}\left(H_{2}(f(t))\right)=S_{T}\left(f(t)^{2}\right)=(f(t-T))^{2}=H_{2}(f(t-T))=H_{2}\left(S_{T}(f(t))\right) \nonumber \]
for all real \(t\). Thus, \(H_2\) is a time invariant system.
Linear Time Invariant Systems
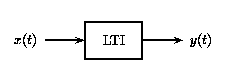
Certain systems are both linear and time-invariant, and are thus referred to as LTI systems.
Linear Time-Invariant Systems
 (a)
(a)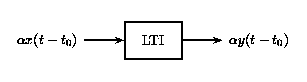 (b)
(b)As LTI systems are a subset of linear systems, they obey the principle of superposition. In the figure below, we see the effect of applying time-invariance to the superposition definition in the linear systems section above.
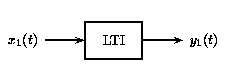 (a)
(a)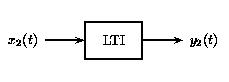 (b)
(b)
Figure \(\PageIndex{8}\)

LTI Systems in Series
If two or more LTI systems are in series with each other, their order can be interchanged without affecting the overall output of the system. Systems in series are also called cascaded systems.
Cascaded LTI Systems
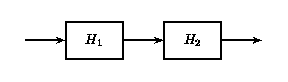 (a)
(a)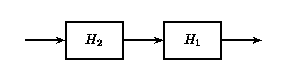 (b)
(b)LTI Systems in Parallel
If two or more LTI systems are in parallel with one another, an equivalent system is one that is defined as the sum of these individual systems.
Parallel LTI Systems
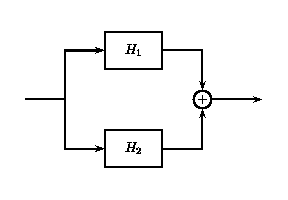 (a)
(a)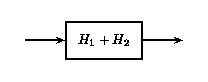 (b)
(b)Example \(\PageIndex{5}\)
Consider the system \(H_3\) in which
\[H_{3}(f(t))=2 f(t) \nonumber \]
for all signals \(f\). Given any two signals \(f\), \(g\) and scalars \(a\), \(b\)
\[\left.H_{3}(a f(t)+b g(t))\right)=2(a f(t)+b g(t))=a 2 f(t)+b 2 g(t)=a H_{3}(f(t))+b H_{3}(g(t)) \nonumber \]
for all real \(t\). Thus, \(H_3\) is a linear system. For all real \(T\) and signals \(f\),
\[S_{T}\left(H_{3}(f(t))\right)=S_{T}(2 f(t))=2 f(t-T)=H_{3}(f(t-T))=H_{3}\left(S_{T}(f(t))\right) \nonumber \]
for all real \(t\). Thus, \(H_3\) is a time invariant system. Therefore, \(H_3\) is a linear time invariant system.
Example \(\PageIndex{6}\)
As has been previously shown, each of the following systems are not linear or not time invariant.
\[H_{1}(f(t))=t f(t) \nonumber \]
\[H_{2}(f(t))=(f(t))^{2} \nonumber \]
Thus, they are not linear time invariant systems.
Linear Time Invariant Demonstration
LTI Systems Summary
Two very important and useful properties of systems have just been described in detail. The first of these, linearity, allows us the knowledge that a sum of input signals produces an output signal that is the summed original output signals and that a scaled input signal produces an output signal scaled from the original output signal. The second of these, time invariance, ensures that time shifts commute with application of the system. In other words, the output signal for a time shifted input is the same as the output signal for the original input signal, except for an identical shift in time. Systems that demonstrate both linearity and time invariance, which are given the acronym LTI systems, are particularly simple to study as these properties allow us to leverage some of the most powerful tools in signal processing.


